Calcolatore per la Radice Cubica

Il nostro calcolatore per la radice cubica è un pratico strumento che ti aiuterà a determinare la radice cubica, detta anche radice terza, di qualsiasi numero positivo. Puoi utilizzare immediatamente il nostro calcolatore: basta digitare il numero di cui vuoi trovare la radice cubica e il gioco è fatto! Inoltre, puoi eseguire i calcoli al contrario e utilizzarli per elevare al cubo i numeri. Per farlo, basta digitare il numero che vuoi elevare alla terza potenza nell'ultimo campo! Può essere estremamente utile durante la ricerca dei cosiddetti cubi perfetti 🇺🇸. Per saperne di più, leggi il seguente articolo.

Grazie al nostro calcolatore per la radice cubica, puoi anche calcolare le radici di altri gradi. Per farlo, devi cambiare il numero nel campo Gradi della radice. Se vuoi saperne di più sulla definizione di radice cubica, familiarizzare con le proprietà della funzione radice cubica e trovare un elenco di cubi perfetti, ti consigliamo di continuare a leggere questo testo. Qui troverai anche alcuni trucchi per trovare la radice cubica usando una calcolatrice o per calcolarla a mente.

Se ti interezza il simbolo di radice, visita il calcolatore per la radice quadrata, dove ne parliamo.

Supponiamo di voler trovare la radice cubica di un numero, x. La radice cubica, y, è un numero che, se elevato alla terza potenza, dà come risultato x. Se lo formuli matematicamente,

∛x = y ⟺ y^3 = x

dove ⟺ è un simbolo matematico che significa se e solo se.

È anche possibile scrivere la radice cubica in un altro modo, che a volte è molto più comodo. La radice cubica è infatti un caso speciale di esponente. Può essere scritta come:

∛(x) = x^(1/3)

Un esempio geometrico può aiutarti a capire questo concetto. L'esempio migliore che possiamo fare è quello del cubo. La radice cubica del volume di un cubo è la lunghezza degli spigoli. Quindi, ad esempio, se un cubo ha un volume di 27 cm³, la lunghezza degli spigoli è uguale alla radice cubica di 27 cm³, ovvero 3 cm. Facile?

Ricorda che nella maggior parte dei casi, la radice cubica non sarà un numero razionale. Questi numeri possono essere espressi come quoziente di due numeri naturali, ovvero una frazione. Le frazioni possono creare delle difficoltà, soprattutto quando si tratta di sommarle. Se hai problemi a lavorare con le frazioni, prova il nostro calcolatore per l'addizione delle frazioni 🇺🇸, che ti aiuterà moltissimo.

È davvero facile trovare la radice cubica di qualsiasi numero positivo con il nostro calcolatore per la radice cubica! Basta digitare un numero qualsiasi per trovare la sua radice cubica. Ad esempio, la radice cubica di 216 è 6. Per l'elenco dei cubi perfetti, vai alla sezione successiva.

Nota che è possibile trovare una radice cubica anche di un numero negativo. Infatti, un numero negativo elevato alla terza potenza è ancora negativo — ad esempio, (-6)³ = -216.

Devi però ricordare che qualsiasi numero non nullo ha tre radici cubiche: almeno una reale e due immaginarie. Questo calcolatore per la radice cubica tratta solo i numeri reali, ma se ti interessa, ti invitiamo a leggere di più sull'argomento dei numeri immaginari!

Di seguito puoi trovare i valori più comuni di radice cubica. Questi numeri sono spesso chiamati anche cubi perfetti perché le loro radici cubiche sono numeri interi. Ecco l'elenco dei primi dieci cubi perfetti:

• Radice cubica di 1: ∛1 = 1, poiché 1 × 1 × 1 = 1;
• Radice cubica di 8: ∛8 = 2, poiché 2 × 2 × 2 = 8;
• Radice cubica di 27: ∛27 = 3, poiché 3 × 3 × 3 = 27;
• Radice cubica di 64: ∛64 = 4, poiché 4 × 4 × 4 = 64;
• Radice cubica di 125: ∛125 = 5, poiché 5 × 5 × 5 = 125;
• Radice cubica di 216: ∛216 = 6, poiché 6 × 6 × 6 = 216;
• Radice cubica di 343: ∛343 = 7, poiché 7 × 7 × 7 = 343;
• Radice cubica di 512: ∛512 = 8, poiché 8 × 8 × 8 = 512;
• Radice cubica di 729: ∛729 = 9, poiché 9 × 9 × 9 = 729; e
• Radice cubica di 1000: ∛1000 = 10, poiché 10 × 10 × 10 = 1000;

Come puoi vedere, i numeri diventano molto grandi velocemente, ma a volte dovrai avere a che fare con numeri ancora più grandi, come i fattoriali. In questo caso, ti consigliamo di utilizzare la notazione scientifica, che è un modo molto più comodo per scrivere numeri molto grandi o molto piccoli.

D'altra parte, la maggior parte degli altri numeri non sono cubi perfetti, ma alcuni di essi vengono comunque utilizzati spesso. Ecco l'elenco di alcuni dei cubi non perfetti, arrotondati ai centesimi:

• Radice cubica di 2: ∛2 ≈ 1,26;
• Radice cubica di 3: ∛3 ≈ 1,44;
• Radice cubica di 4: ∛4 ≈ 1,59;
• Radice cubica di 5: ∛5 ≈ 1,71;
• Radice cubica di 10: ∛10 ≈ 2,15;

Non esitare a utilizzare il nostro calcolatore per la radice cubica se il numero che vuoi e di cui hai bisogno non è presente in questa lista!

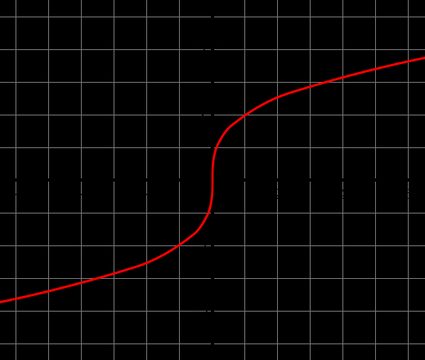
Puoi tracciare il grafico della funzione y = ∛(x). A differenza, ad esempio, della funzione logaritmica, la funzione radice cubo è una funzione dispari — ciò significa che è simmetrica rispetto all'origine e soddisfa la condizione - f(x) = f(-x). Anche questa funzione passa per lo zero.

Grazie a questa funzione, puoi disegnare il grafico della radice cubica, mostrato qui sotto. Ti invitiamo anche a dare un'occhiata al calcolatore per la formula quadratica 🇺🇸 per vedere altre formule di funzioni!

Pensi che sia possibile risolvere semplici problemi con le radici cubiche senza un calcolatore online, o anche senza carta e penna? Se pensi che sia impossibile o che tu non sia in grado di farlo, dai un'occhiata a questo metodo: è molto semplice. Tuttavia, funziona solo per i cubi perfetti. Dimentica tutte le regole dei libri di aritmetica e considera per un momento il seguente metodo descritto da Robert Kelly.

Prima di tutto, è fondamentale memorizzare i cubi dei numeri da 1 a 10 e l'ultima cifra dei loro cubi. La tabella che segue lo illustra.

Quando hai un numero di cui vuoi trovare la radice cubica, guarda prima le migliaia (salta le ultime tre cifre). Ad esempio, per il numero 185 193, le migliaia sono 185. 5 elevato al cubo è 125 e 6 è 216. È quindi ovvio che il numero che stai cercando è compreso tra 50 e 60. Il passo successivo consiste nell'ignorare tutte le altre cifre tranne l'ultima. Possiamo vedere che è 3, quindi controlla la tua memoria o la nostra tabella. Scoprirai che il numero che stai cercando è 7. Quindi la risposta è 57! Facile?

Facciamo un altro esempio e procediamo passo dopo passo!

1. Pensa al numero che vuoi conoscere come a una radice cubica. Prendiamo 17 576;
2. Salta le ultime tre cifre;
3. Trova le due radici cubiche più vicine che conosci. La radice cubica di 8 è 2 e la radice cubica di 27 è 3. Quindi il tuo numero è compreso tra 20 e 30;
4. Guarda l'ultima cifra. L'ultima cifra di 17 576 è 6;
5. Usa la tua memoria (o la nostra tabella): l'ultima cifra 6 corrisponde al numero 6. Questa è l'ultima cifra del tuo numero; e
6. Combina i due numeri: 26. Questa è la radice cubica di 17 576!

Ti ricordiamo che questo algoritmo funziona solo per i cubi perfetti! E la probabilità che un numero casuale sia un cubo perfetto è, ahimè, molto bassa. Hai solo lo 0,0091% di possibilità di trovarne uno tra 1000 e 1 000 000. Se non ti fidi del tuo risultato, dimentica questa regola e usa il nostro calcolatore per la radice cubica :-)

1. Per prima cosa, devi digitare il numero per il quale devi trovare la radice cubica;
2. Premi √ (tasto radice) due volte;
3. Premi × (segno di moltiplicazione);
4. Premi √ (tasto radice) quattro volte;
5. Premi × (segno di moltiplicazione);
6. Premi √ (tasto radice) otto volte;
7. Premi × (segno di moltiplicazione);
8. Un'ultima volta, premi il tasto √ (tasto radice) due volte; e
9. E ora puoi premere = (segno di uguale)! Ecco la tua risposta!

Non ci credi? Controlla ancora una volta con un altro esempio!

Supponiamo che tu debba fare una palla con un volume di 33,5 mL. Per prepararla devi conoscere il suo raggio. Come probabilmente saprai, l'equazione per calcolare il volume di una sfera è la seguente:

V = (4/3) * π * r³

Quindi l'equazione per il raggio è la seguente:

r = ∛(3V/4π)

Sai che il volume è di 33,5 mL. All'inizio è necessario passare a diverse unità di misura del volume. La conversione più semplice è quella in cm³: 33,5 mL = 33,5 cm³. Ora puoi risolvere il raggio:

r = ∛(100,5/12,56)

r = ∛(8)

r = 2

Affinché una palla abbia un volume di 33,5 mL, il suo raggio deve essere di 2 centimetri.

Con il nostro calcolatore per radici puoi calcolare anche altre radici. Basta scrivere il numero nel campo Grado della radice e riceverai una radice ennesima a scelta. Il nostro calcolatore eseguirà automaticamente tutti i calcoli necessari e potrai utilizzarlo liberamente nei tuoi calcoli!

Facciamo qualche esempio. Supponiamo che tu debba calcolare la radice quarta di 1296. Per prima cosa, devi scrivere il numero di cui vuoi trovare la radice — 1296. Poi cambia il grado della radice in 4. Ed ecco il risultato! La quarta radice di 1296 è 6.

Il nostro calcolatore per la radice ennesima ti permette anche di calcolare la radice dei numeri irrazionali. Proviamo a calcolare la radice π-esima. Il simbolo π rappresenta il rapporto tra la circonferenza di un cerchio e il suo diametro. Il suo valore è costante per ogni cerchio ed è approssimativamente 3,14, ma puoi usare il nostro calcolatore del rapporto 🇺🇸 per trovare il suo valore più preciso!

Supponiamo che tu voglia calcolare la radice π-esima di 450. Per prima cosa, scrivi 450 nel campo Numero. Poi cambia il Grado della radice: arrotonda e scrivi 3,14 invece di π. Ora puoi vedere il risultato. È quasi 7.

Alla fine di questo articolo, abbiamo preparato una sezione di matematica avanzata per i più tenaci. Probabilmente saprai che i numeri positivi hanno sempre due radici quadrate: una negativa e una positiva. Ad esempio, √4 = -2 e √4 = 2. Ma sapevi che una regola simile si applica anche alle radici cubiche? Tutti i numeri reali (tranne lo zero) hanno esattamente tre radici cubiche: un numero reale e una coppia di numeri complessi. I numeri complessi sono stati introdotti dai matematici molto tempo fa per spiegare problemi che i numeri reali non possono risolvere. Di solito li esprimiamo con la seguente forma:

x = a + b × i,

dove x è il numero complesso con la parte reale a e immaginaria b (per i numeri reali, b = 0). Il misterioso numero immaginario i è definito come la radice quadrata di -1:

i = √(-1)

Bene, ma come influisce questa conoscenza sul numero di soluzioni della radice cubica? A titolo di esempio, considera le radici cubiche di 8, che sono 2, -1 + i√3 e -1 - i√3. Se non ci credi, verifichiamolo elevandole a potenza di 3, ricordando che i² = -1 e utilizzando la formula della moltiplicazione breve (a + b)³ = a³ + 3a²b + 3ab² + b³:

1. 2³ = 8 — la più ovvia;
2. (-1 + i√3)³ = -1 + 3i√3 + 9 - 3i√3 = 8; e
3. (-1 - i√3)³ = -1 - 3i√3 + 9 + 3i√3 = 8.

Lo vedi ora? Sono tutti uguali a 8!

La radice cubica di un prodotto di due numeri è il prodotto delle radici cubiche di questi numeri. La formula è quindi ∛(a × b) = ∛a × ∛b.

La risposta è -2/3. Per ottenere questo risultato, procedi come segue:

1. Ricorda la formula ∛(a / b) = ∛a / ∛b;
2. Calcola la radice cubica di -8. Chiaramente, ∛(-8) = -2;
3. Calcola la radice cubica di 27: abbiamo ∛27 = 3; e
4. Il risultato finale è -2/3. Ben fatto!

Il codice Alt per il simbolo della radice cubica ∛ è 8731. Cioè, per produrre ∛, procedi come segue:

1. Assicurati che il Num Lock sia attivo;
2. Premi uno dei tasti Alt;
3. Tenendo premuto il tasto Alt, digita il codice 8731 utilizzando il tastierino numerico;
4. Lascia il tasto Alt. Apparirà il simbolo della radice cubica; oppure
5. Come metodo alternativo: copia il simbolo ∛ (Ctrl+C) e incollalo dove ti serve (Ctrl+V).