Kalkulator wycinka kołowego

Za pomocą tego kalkulatora wycinka kołowego szybko znajdziesz pole dowolnego wycinka kołowego, np. pole półkola lub ćwiartki koła. W tym krótkim artykule:

• Podamy definicję wycinka kołowego i wyjaśnimy, czym jest wycinek kołowy.

• Pokażemy wzór na pole wycinka kołowego i wytłumaczymy, jak samodzielnie wyprowadzić równanie bez większego wysiłku.

• Przedstawimy kilka przykładów z życia wziętych, w których kalkulator wycinka kołowego może okazać się przydatny.

Zacznijmy więc od definicji wycinka — czym jest wycinek kołowy w geometrii?

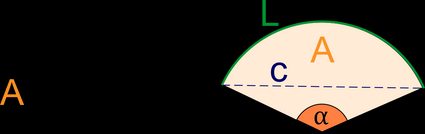
Wycinek kołowy (wycinek koła) to figura geometryczna ograniczona dwoma promieniami i łukiem okręgu.

Wycinki kołowe są najczęściej wizualizowane za pomocą wykresów kołowych, gdzie koło jest podzielone na kilka części, aby pokazać wagę każdego segmentu. Poniższe ilustracje przedstawiają kilka przykładów wycinków kołowych — niekoniecznie oznacza to, że będą one wyglądać jak kawałek ciasta, ale czasami wyglądają jak reszta ciasta po wycięciu kawałka:

Bardzo rzadko można też usłyszeć o wycinku elipsy, jednak wzory te są znacznie, znacznie trudniejsze w użyciu niż równania na pole wycinka kołowego.

Wzór na pole wycinka kołowego jest prosty — należy pomnożyć kąt środkowy przez kwadrat promienia i podzielić przez 2:

• Pole wycinka kołowego = r² ⋅ α / 2

Ale, tak właściwie, to skąd się ten wzór bierze? Można go określić dzięki proporcjom. Wszystko, o czym musisz pamiętać, to wzór na pole koła (a założymy się, że go pamiętasz!):

1. Pole koła oblicza się jako A = πr². To świetny punkt wyjścia.

2. Kąt pełny to 2π w radianach lub 360° w stopniach, z czego ta druga jednostka jest bardziej powszechna.

3. Następnie chcemy obliczyć pole części okręgu, wyrażone przez kąt środkowy.

   • Dla kątów 2π (pełny okrąg), pole jest równe πr²:

     2π → πr²

   • Jakie jest więc pole wycinka kołowego?

     α → pole wycinka kołowego

4. Z proporcji możemy łatwo znaleźć ostateczny wzór na pole wycinka kołowego:

   Pole wycinka kołowego = α ⋅ πr² / 2π = α ⋅ r² / 2

Tej samej metody można użyć do znalezienia długości łuku — wystarczy zapamiętać wzór na obwód okręgu. Przeczytaj więcej na ten temat w naszym kalkulatorze obwodu oraz kalkulatorze długości łuku.

Znalezienie pola półkola lub ćwiartki koła powinno być teraz dla ciebie bułką z masłem. Przecież wystarczy się tylko zastanowić, jaką są one częścią koła!

1. Pole półkola: πr² / 2

• Wiedząc, że półkole jest połową okręgu, podziel pole koła przez 2:

  Pole półkola = Pole koła / 2 = πr² / 2

• Oczywiście ten sam wynik uzyskasz używając wzoru na pole wycinka kołowego. Wystarczy tylko pamiętać, że kąt prosty wynosi π (180°):

  Pole półkola = α ⋅ r² / 2 = πr² / 2

• Ponieważ ćwiartka koła jest 1/4 koła, możemy zapisać ten wzór jako:

  Pole ćwiartki koła = pole koła / 4 = πr² / 4

• Kąt środkowy ćwiartki koła jest kątem prostym (π/2 lub 90°), więc szybko dojdziemy do tego samego równania:

  Pole ćwiartki koła= α ⋅ r² / 2 = πr² / 4

Wiemy, wiemy, słyszeliśmy to nie raz: „Po co mamy się tego uczyć? Nigdy tego nie użyjemy”. Cóż, chcielibyśmy wam pokazać, że geometria jest dosłownie wszędzie wokół nas:

• Jeśli zastanawiasz się, jak duży tort powinieneś zamówić na swoje niesamowite przyjęcie urodzinowe — bingo, to jest właśnie to! Użyj wzoru na wycinek kołowy, aby oszacować rozmiar kawałka 🍰 dla swoich gości, aby nikt nie umarł z głodu.

• Podobnie jest z pizzą — czy zauważyłeś, że każdy kawałek jest wycinkiem kołowym okręgu 🍕? Na przykład, jeśli nie jesteś wielkim fanem brzegów pizzy, możesz obliczyć, który rozmiar pizzy da ci najlepszą ofertę.

• A może czyta nas jakiś entuzjasta szycia? 👗 Obliczenia powierzchni wycinka kołowego mogą być przydatne podczas przygotowywania spódnicy z koła (ponieważ nie zawsze jest to pełne koło, ale, no wiesz, właśnie wycinek koła).

Oprócz tych prostych, rzeczywistych przykładów, wzór na pole wycinka kołowego może być przydatny w geometrii, np. do znalezienia pola powierzchni stożka.