Calculadora de Cargas de Vigas

A calculadora de cargas de vigas da Omni ajudará você a determinar as reações nos apoios de uma viga simplesmente apoiada devido a cargas pontuais verticais ou forças 🇺🇸. Nesta calculadora, exploraremos o seguinte:

• O que é reação de apoio;
• Como calcular as reações de apoio em uma viga;
• Exemplo de cálculo de como encontrar reações de apoio; e
• Como calcular a capacidade de carga da viga usando esta calculadora de cargas de vigas.

Se você souber como encontrar reações de apoio, é um ótimo ponto de partida para analisar vigas, por exemplo, ao determinar a deflexão da viga. Continue lendo para saber mais.

De acordo com a terceira lei do movimento de Newton, toda força sobre um objeto tem uma reação igual e oposta. Se você tentar empurrar algo, digamos uma parede, parece que a parede também está empurrando de volta para você. Esse é exatamente o fenômeno que a terceira lei do movimento de Newton descreve.

Na engenharia, os membros estruturais, como vigas e colunas, interagem uns com os outros nos pontos em que se encontram. Imagine uma viga que está sendo apoiada no lugar por duas colunas. O peso da viga empurra as colunas para baixo e, devido à terceira lei do movimento de Newton, também podemos dizer que as colunas exercem uma força de reação oposta equivalente na viga. Chamamos essas forças de reação de reações de apoio.

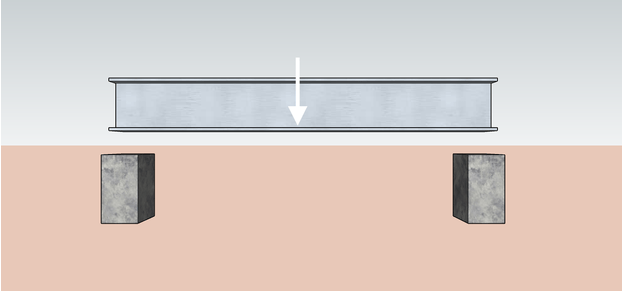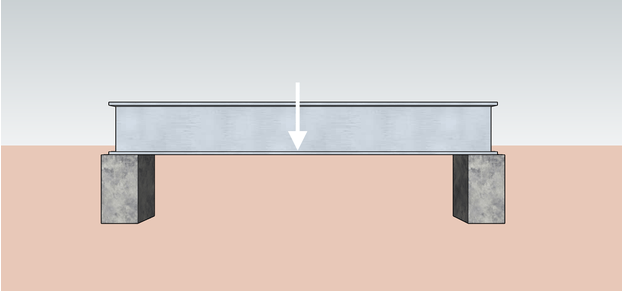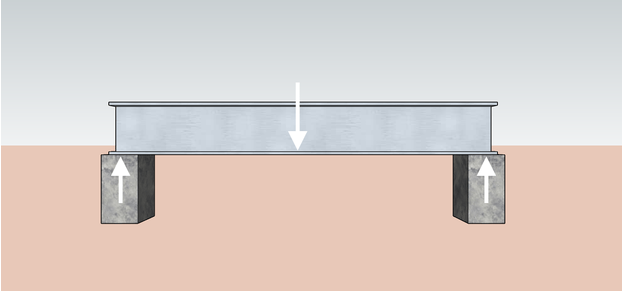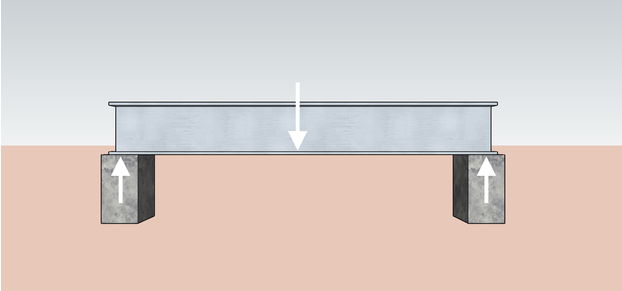
Você pode imaginar um lintel como a viga mostrada acima e os dois pinos de encaixe (os pinos verticais onde o lintel se apoia) como as duas estruturas de apoio do lintel. Para saber mais sobre os tamanhos de lintel possíveis, consulte nossa calculadora de tamanho de lintel 🇺🇸.

Em uma viga com apoio simples, as reações de apoio em cada extremidade da viga podem ser iguais entre si ou de valores diferentes. Seus valores dependem das cargas aplicadas na viga. Se mais cargas forem encontradas em uma distância mais próxima de um suporte, esta estrutura de apoio sofrerá mais força e, portanto, uma reação maior.

Como as reações de apoio atuam na direção oposta à da força, podemos dizer que todo o sistema está em equilíbrio. Isso significa que a viga não está se movendo, e a soma das forças e dos momentos resulta em zero. Ao igualar os momentos devidos à carga aos momentos devidos às reações de apoio, podemos determinar as reações nos apoios.

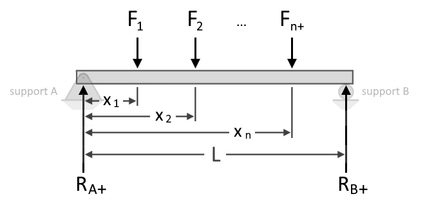
Assim como no cálculo do torque, também podemos realizar uma soma dos momentos em cada apoio para resolver as reações. Abaixo, expressamos uma soma, $\small \sum$, dos momentos no apoio A para encontrar a reação no apoio B, denotada como $\small R_\text{B}$, conforme mostrado abaixo:

ou

onde:

• $F_1$, $F_2$, $F_3$, e $F_n$ são as cargas pontuais na viga a distâncias $x_1$, $x_2$, $x_3$, e $x_n$, do apoio A, respectivamente;
• $R_\text{B}$ é a reação no apoio B; e
• $\text{vão}$ é o comprimento da viga entre o apoio A e o apoio B.

Reorganizando a equação, podemos isolar $R_\text{B}$ da seguinte forma:

Agora que temos uma expressão para encontrar $\small R_\text{B}$, e como sabemos que o total das forças aplicadas é igual ao total das reações, também podemos encontrar a reação no apoio A, $\small R_\text{A}$, usando as seguintes equações:

Agora que sabemos como calcular as reações de apoio em vigas, vamos considerar um exemplo de cálculo para reforçar nosso conhecimento sobre isso. 🙂

Suponha que você tenha uma viga de apoio simples de 4,0 metros de comprimento com uma carga pontual aplicada de 10,0 quilonewtons (kN) a 2,0 metros do apoio A e outra carga pontual aplicada de 3,5 kN a 1,5 metros do apoio B, conforme mostrado abaixo:

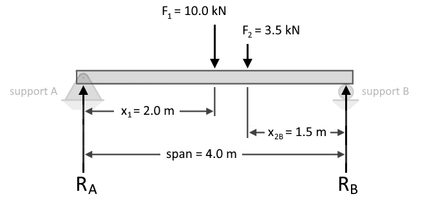
Para calcular para $\small R_\text{B}$, formulamos a equação de equilíbrio de momento da seguinte forma:

Ao realizar uma soma de forças, obtemos:

Observe que, para esse somatório, consideramos todas as forças descendentes como positivas e todas as forças ascendentes como negativas. Baseado em nossos cálculos acima, obtivemos agora que as reações nos apoios A e B são 6,3125 kN e 7,1875 kN, respectivamente.

Além disso, observe que, neste exemplo de como encontrar reações de apoio e na calculadora de cargas de vigas, presumimos que a viga não tem peso. No entanto, se o peso da viga for indicado, você poderá considerar o peso da viga como outra carga pontual descendente no centro, ou centroide, da viga.

Nossa calculadora é fácil e simples de usar. Tudo o que você precisa fazer é inserir o vão da viga, a magnitude das cargas pontuais e suas distâncias do apoio A. A princípio, você verá apenas campos para duas cargas (Carga 1 e Carga 2), mas assim que inserir um valor para $\small x_2$, os campos para a Carga 3 serão exibidos, e assim sucessivamente.

Se você quiser inserir uma carga ascendente, basta inserir um valor negativo para a magnitude da carga. No total, você pode inserir até 11 cargas pontuais em nossa calculadora de cargas de vigas.

Uma viga simplesmente apoiada é uma viga que tem dois apoios localizados em cada extremidade. Um apoio é um suporte com pinos, que permite apenas um grau de liberdade, a rotação em torno do eixo z (perpendicular ao papel). Na outra extremidade, há um apoio de roletes, que permite dois graus de liberdade, o movimento horizontal ao longo do eixo x e a rotação em torno do eixo z perpendicular.

Para determinar as reações em uma viga simplesmente apoiada:

1. Desenhe o diagrama de corpo livre da viga.

2. Some os momentos em um apoio, como o apoio de pino A:

   Σ(F_i × x_i) - R_yB × vão da viga = 0

   onde:

   • F_i: forças verticais;
   • x_i: distância entre A e a carga pontual; e
   • R_yB: reação vertical no apoio de roletes B.

3. Para encontrar a reação vertical em A, R_yA, some as forças verticais:

   ΣF_y = ΣF_i - R_yB - R_yA = 0.

4. Some as forças horizontais para encontrar a reação horizontal em A R_xA:

   ΣF_y = ΣF_i - R_xA = 0.

A calculadora das reações de apoio é essencial para compreender as forças internas em uma viga. No projeto da viga, precisamos entender como as forças de cisalhamento internas e os momentos de flexão se comportam. Ao saber como essas cargas variam ao longo da viga, podemos analisar e prever com precisão as tensões e deformações resultantes, o que nos ajuda a projetar vigas capazes de suportar essas condições, garantindo a integridade e a segurança estrutural.

Para uma viga com uma carga de peso uniformemente distribuída de 5 kN/m, as reações em A e B são ambas de 15 kN. Para que você calcule isso:

1. Desenhe o diagrama de corpo livre da viga, incluindo a carga pontual equivalente ao peso.

2. Some os momentos no apoio de pino A para encontrar a reação vertical no apoio de rolete B:

   R_yB = 30 kN ⋅ 3 m/6 m = 15 kN.

3. Some as forças verticais para encontrar a reação vertical em A:

   R_yA = 30 kN - 15 kN = 15 kN.

4. A reação horizontal no apoio A, R_xA, é zero.