Calculadora de Deflexão de Vigas
Índice
O que é deformação e flexão de viga?Como calcular a deflexão máxima da vigaMétodo de superposiçãoRigidez da vigaEntendendo as fórmulas de deflexão da vigaCálculo da deflexão de uma vigaPerguntas frequentesEsta calculadora de deflexão de vigas da Omni ajudará você a determinar a deflexão máxima de viga de vigas simplesmente apoiadas ou vigas em balanço sujeitas a aplicação de carga simples.
Você pode escolher entre uma seleção de tipos de carga que podem atuar em qualquer comprimento de viga que desejar. A magnitude e a localização dessas cargas afetam o quanto a viga se deforma.
Nesta calculadora de deflexão de vigas, você aprenderá sobre as diferentes fórmulas de deflexão de viga usadas para calcular deflexões de viga com apoio simples e deflexões de viga em balanço. Você também aprenderá como o módulo de elasticidade da viga e o momento de inércia da sua seção transversal afetam a deflexão máxima calculada da viga.
A deformação, ou deflexão, da viga é uma parte importante da análise de vigas, mas outra parte importante é a análise de tensão, através do momento fletor. O módulo de seção é uma ferramenta poderosa para estudar as tensões de flexão da viga, que você pode calcular usando a calculadora de módulo de seção da Omni.
O que é deformação e flexão de viga?
Na construção de edifícios, geralmente usamos estruturas de armação que são mantidas no lugar pelas fundações no solo. Essas estruturas de armação são como os esqueletos de edifícios, casas e até mesmo pontes. Em uma estrutura, chamamos as estruturas verticais de colunas e as horizontais de vigas. As vigas são os membros estendidos de uma estrutura que carregam as cargas das lajes das estruturas, como pisos de concreto sólido, madeira e telhados.
Quando as vigas carregam cargas pesadas demais para elas, começam a se flexionar. Podemos chamar a flexão de deflexão da viga. A deflexão da viga é o deslocamento vertical de um ponto ao longo do centroide de uma viga. Também podemos considerar a superfície da viga como nosso ponto de referência, desde que não haja alterações na altura ou profundidade da viga durante a flexão.
Como calcular a deflexão máxima da viga
Equipamos nossa calculadora de deflexão de viga com as fórmulas que os engenheiros e estudantes de engenharia usam para determinar rapidamente a deflexão máxima que uma viga específica sofrerá devido à carga que carrega. Entretanto, essas fórmulas só podem resolver cargas simples e uma combinação dessas cargas. Tabulamos essas fórmulas para você, conforme mostrado abaixo:
Fórmulas de deflexão para vigas simplesmente apoiadas
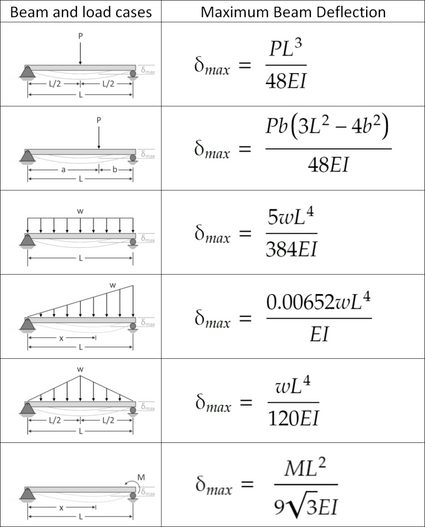
Fórmulas de deflexão para vigas em balanço
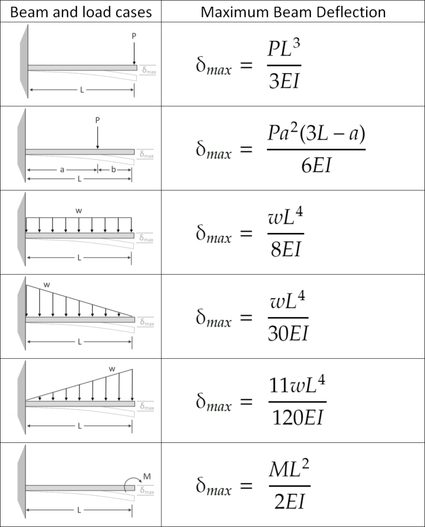
Método de superposição
Para calcular a deflexão máxima de uma viga com uma combinação de cargas, podemos usar o método da superposição. O método de superposição afirma que podemos aproximar a deflexão total de uma viga somando todas as deflexões provocadas por cada configuração de carga. Entretanto, esse método nos dá apenas um valor aproximado para a deflexão máxima real. O cálculo de cargas complicadas exigiria que você use o que é conhecido como método de integração dupla.
Rigidez da viga
Para calcular a deflexão da viga, você precisa conhecer a rigidez da viga e a quantidade de força ou carga que influenciaria a flexão da viga. Podemos definir a rigidez da viga multiplicando o módulo de elasticidade da viga, E, por seu momento de inércia, I.
O módulo de elasticidade depende do material da viga. Quanto mais alto for o módulo de elasticidade de um material, mais uma deflexão poderá sustentar cargas enormes antes de atingir seu ponto de ruptura. O módulo de elasticidade do concreto está entre 15 e 50 GPa (gigapascal), enquanto o aço tende a estar em torno de 200 GPa ou mais. Essa diferença nos valores do módulo de elasticidade mostra que o concreto pode suportar apenas uma pequena quantidade de deflexão e sofrerá rachaduras mais cedo do que o aço.
Você pode saber mais sobre o módulo de elasticidade consultando a calculadora de tensão mecânica da Omni. Por outro lado, para determinar o momento de inércia de uma seção transversal de uma viga específica, você pode visitar a calculadora de momento de inércia, também da Omni. O momento de inércia representa a quantidade de resistência que um material tem ao movimento rotacional. O momento de inércia depende das dimensões da seção transversal do material.
O momento de inércia também varia dependendo do eixo em que o material está girando. Para entender melhor esse conceito, vamos considerar a seção transversal de uma viga retangular com largura de 20 cm e altura de 30 cm. Usando as fórmulas que você também pode ver em nossa calculadora de momento de inércia, podemos calcular os valores do momento de inércia dessa seção transversal da viga da seguinte forma:
Iₓ = largura × altura³ / 12
Iₓ = 20⋅(30³)/12
Iₓ = 45.000 cm⁴
Iᵧ = altura × largura³ / 12
Iᵧ = 30⋅(20³)/12
Iᵧ = 20.000 cm⁴
Observe como há dois valores para o momento de inércia. Isso ocorre porque podemos considerar que a viga se deforma verticalmente ao longo do eixo x (ou sofre um momento de flexão ao redor do eixo x) e lateralmente ao longo do eixo y (ou se dobra ao redor do eixo y). Como estamos considerando a deflexão da viga quando ela se deforma verticalmente ou em torno do eixo x, temos que usar Iₓ para nossos cálculos.
Os valores do momento de inércia que obtivemos nos dizem que a viga é mais difícil de deformar com uma carga vertical e mais fácil de deformar se for submetida a uma carga lateral horizontal. Essa diferença nos valores do momento de inércia é a razão pela qual vemos vigas nessa configuração, ou seja, com altura maior que a largura.
Entendendo as fórmulas de deflexão da viga
Agora que conhecemos os conceitos de módulo de elasticidade e momento de inércia, podemos entender por que essas variáveis são os denominadores em nossas fórmulas de deflexão de viga. As fórmulas mostram que quanto mais rígida for a viga, menor será sua deflexão. Entretanto, ao inspecionar nossas fórmulas, também podemos dizer que o comprimento da viga também afeta diretamente a sua deflexão. Quanto mais longa for a viga, mais ela poderá se deformar e maior será essa deformação.
As cargas, por outro lado, afetam a deflexão da viga de duas maneiras: a direção da deflexão e a magnitude da deflexão. As cargas descendentes tendem a flexionar a viga para baixo. As cargas podem ser na forma de carga de ponto único, carregamento linear ou momento fletor. As fórmulas desta calculadora se concentram apenas nas direções para baixo ou para cima para a carga pontual e para carregamentos distribuídos, não considerando forças ou carregamentos aplicados na horizontal. Cabe lembrar que os carregamentos distribuídos são semelhantes à carga em um único ponto, mas consideram todo o comprimento da viga.
As fórmulas desta calculadora também consideram o momento fletor, seja no sentido horário ou anti-horário. Basta consultar as direções das setas na imagem correspondente da fórmula para descobrir em quais direções há um valor de carga positivo.
Cálculo da deflexão de uma viga
Para um exemplo de cálculo de deflexão de viga, vamos considerar um banco de madeira simples com seus apoios a 1,5 metro de distância entre si. Digamos que você tenha uma prancha de madeira de 4 cm de espessura e 30 cm de largura que sirva de assento para esse banco. Podemos considerar esse assento como uma viga que sofrerá deflexão sempre que alguém se sentar no banco. Dadas as dimensões desse assento, podemos calcular seu momento de inércia, de forma semelhante ao exemplo acima. Como precisamos calcular Iₓ, seu momento de inércia seria:
Iₓ = largura × altura³ / 12
Iₓ = 30⋅(4³)/12
Iₓ = 160,0 cm⁴ ou 1,6⋅10-⁶ m⁴
Vamos considerar que a madeira do banco possua módulo de elasticidade de 6.800 MPa (6,8×10⁹ Pa). Você pode fazer uma busca na internet e obter facilmente o valor do módulo de elasticidade da madeira (desde que você saiba o tipo de madeira), ou de qualquer outro material, como aço e concreto. Agora que conhecemos esses valores, consideremos a carga que esse banco suportará. Suponha que uma criança de 400 N se sente no meio do banco. Agora podemos calcular a deflexão que o assento do banco sofrerá devido a uma carga pontual em seu centro:
δmax = P⋅L³ / (48⋅E⋅I)
δmax = (400 N) × (1,5 m)³ / (48⋅6,8⋅10⁹ Pa⋅1,6⋅10-⁶ m⁴)
δmax = 0,002585 m = 2,5850 mm
Isso significa que o assento do banco poderá flexionar cerca de 2,6 milímetros em relação à sua posição original quando alguém se sentar no meio do banco.
Se você achou este tópico interessante e gostaria de saber mais sobre a resistência dos materiais, talvez também goste da calculadora de fator de segurança 🇺🇸 da Omni.
O que é deflexão na engenharia?
A deflexão em engenharia refere-se ao movimento de uma viga em relação à sua posição original. Esse movimento pode vir de forças, seja do peso próprio ou de uma fonte externa, como o peso das paredes ou do teto. A deflexão na engenharia é uma medida de comprimento porque, quando você calcula a deflexão de uma viga, obtém um ângulo ou distância que se relaciona à distância do movimento da viga.
Qual é a fórmula geral para a deflexão da viga?
As fórmulas gerais para a deflexão de viga são PL³/(3EI) para vigas em balanço e 5wL⁴/(384EI) para vigas simplesmente apoiadas, em que P é a carga pontual, L é o comprimento da viga, E representa o módulo de elasticidade e I refere-se ao momento de inércia. No entanto, muitas outras fórmulas de deflexão permitem que os usuários meçam tipos diferentes de vigas e deflexão.
Como calcular a deflexão de uma viga?
Para calcular a deflexão de uma viga, siga estas etapas:
- Determine se é uma viga em balanço ou uma viga com suporte simples.
- Meça a deformação da viga a partir da deformação da estrutura.
- Escolha a fórmula de deflexão de viga apropriada para o tipo de viga que você tem.
- Insira seus dados, incluindo o comprimento da viga, o momento de inércia, o módulo de elasticidade e a força atuante.
O que causa a deflexão em vigas?
As principais causas da deflexão são a sobrecarga, o momento de inércia,que é o tamanho da seção transversal, o comprimento da estrutura sem suporte e o material da estrutura.
Qual é a deflexão central de uma viga simplesmente apoiada com um vão de 4 m?
3,47 mm. Isso se o comprimento (L) for 4 m = 4 × 10³ mm, a carga pontual (P) for 45 × 10³ N, o módulo de elasticidade (E) for 2,4 × 10⁵ N/mm² e o momento de inércia (I) for 72 × 10⁶ mm⁴. Para calcular isso:
- Escolha a fórmula: PL³/(48EI).
- Insira os valores:
45⋅10³(4⋅10³)³/(48⋅2,4⋅10⁵⋅72⋅10⁶) = 3,47 mm.
