Calculadora da Lei de Snell

Quando a luz passa de um meio para outro, ela se curva ou refrata. A calculadora da Lei de Snell da Omni permite que você explore esse tópico em detalhes e entenda os princípios da refração. Continue lendo para descobrir como a Lei de Refração de Snell é formulada e qual equação permitirá que você calcule o ângulo de refração. A última parte deste artigo é dedicada à fórmula e à definição do ângulo crítico.

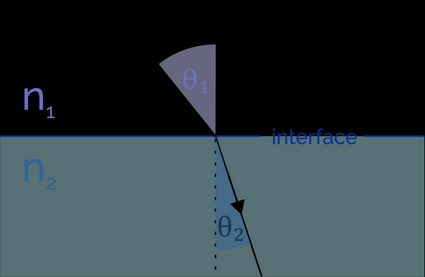
A lei de Snell descreve exatamente como a refração funciona. Quando um raio de luz entra em um meio diferente, sua velocidade e comprimento de onda mudam. O raio se curva em direção à normal dos limites dos dois meios (quando sua velocidade diminui) ou se afasta dela (quando sua velocidade aumenta). O ângulo de refração depende dos índices de refração de ambos os meios:

onde:

• $n_1$: índice de refração do meio 1 (a partir do qual o raio viaja);
• $n_2$: índice de refração do meio 2 (para o qual o raio se desloca);
• $\theta_1$: ângulo de incidência, sendo este o ângulo entre uma linha normal (perpendicular) ao limite entre dois meios e o raio que chega; e
• $\theta_2$: ângulo de refração, sendo este o ângulo entre a normal à fronteira e o raio que atravessa o meio 2.

Você pode encontrar alguns dos valores de $n_1$ e $n_2$ para meios comuns na nossa calculadora de índice de refração.

Em geral, a lei de refração de Snell só é válida para meios isotrópicos. Em meios anisotrópicos, como os cristais, o raio pode ser dividido em dois raios.

Vamos supor que você queira encontrar o ângulo de refração de um feixe de luz que passa do ar para o vidro. O ângulo de incidência é de 30°.

1. Encontre o índice de refração do ar. Ele é igual a $1,\!000293$.
2. Encontre o índice de refração do vidro. Vamos supor que ele seja igual a $1,\!50$.
3. Transforme a equação de modo que a incógnita (ângulo de refração) fique no lado esquerdo:

$\mathrm{sen}(\theta_2) = \frac{n_1 \mathrm{sen}(\theta_1)}{n_2}$
4. Faça os cálculos:
$\mathrm{sen}(\theta_2) = \frac{1,000293 \cdot \mathrm{sen}(30\degree)}{1,50} = 0,\!333$
5. Encontre o arcsen desse valor:
$\theta_2 = \mathrm{arcsen}(0,\!333) = 19,\!48 \degree$
6. Você também pode economizar tempo e simplesmente usar a calculadora da Lei de Snell.

Às vezes, ao aplicar a Lei de Refração de Snell, você receberá o $\mathrm{sen}(\theta_2)$ como um valor maior que 1. Isso é, obviamente, impossível. Se isso acontecer, significa que toda a luz é refletida a partir do ângulo limite (esse fenômeno é conhecido como reflexão interna total). A nossa calculadora de Lei de Refração de Snell informará você quando isso acontecer.

O maior ângulo de incidência, para o qual a luz não é refletida, é chamado de ângulo crítico. O raio refratado viaja ao longo da fronteira entre os dois meios. Isso significa que o ângulo de refração é igual a 90°. Portanto, você pode encontrar o ângulo crítico usando a seguinte equação:

Após a simplificação, $n_1 \mathrm{sen}(\theta_1) = n_2 \cdot 1$.

Resolvendo para o ângulo de incidência temos, $\theta_1 = \mathrm{arcsen}(\frac{n_2}{n_1})$.