Calculadora da Altura de um Triângulo
Se você está procurando uma ferramenta fácil para calcular a altura de qualquer triângulo, você está no lugar certo, pois essa calculadora da altura de um triângulo da Omni vai te ajudar com isso. Se você está procurando as fórmulas de altura de triângulos especiais, como o triângulo retângulo, equilátero, isósceles, ou qualquer triângulo escaleno, essa calculadora é uma aposta segura. Com ela você pode calcular as alturas do triângulo, bem como os lados, os ângulos, o perímetro e a área do triângulo. Experimente!
Se você ainda estiver se perguntando sobre a fórmula para a altura de um triângulo equilátero ou como encontrar a altura sem ter a área, continue lendo e você encontrará a resposta.
Qual é a altura de um triângulo?
Cada lado do triângulo pode ser uma base e, a partir de cada vértice, você pode traçar uma reta perpendicular até uma linha que contém a base. Essa é a altura do triângulo! Como todo triângulo tem três lados, logo, possuem três alturas também.
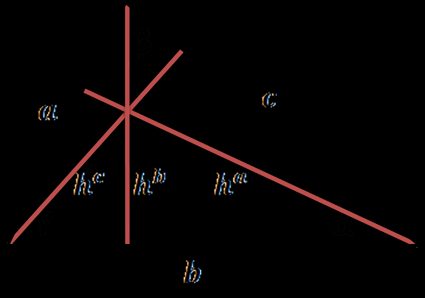
Como encontrar a altura de um triângulo: fórmulas
Há muitas maneiras de encontrar a altura do triângulo. A mais popular é a que usa a área do triângulo, mas existem muitas outras fórmulas:
-
Dada a área do triângulo
A conhecida equação para a área de um triângulo pode ser transformada em uma fórmula para a altura de um triângulo retângulo:
-
, em que é base e é a altura; e
-
Portanto, .
Mas como encontrar a altura de um triângulo sem conhecer sua área? As fórmulas mais populares são:
-
-
Dados os lados do triângulo
O uso de uma equação chamada fórmula de Heron permite que você calcule a área, dados os lados do triângulo. Então, depois de saber a área, você pode usar a equação básica para descobrir qual é a altura de um triângulo:
Fórmula de Heron:
Portanto:
Você pode saber mais sobre essa equação com a calculadora da fórmula de Heron 🇺🇸, também da Omni.
-
Dados dois lados e o ângulo entre eles
Use a trigonometria ou outra fórmula para calcular a área de um triângulo:
(ou ou se você tiver lados diferentes):
Se sua forma for um tipo especial de triângulo, veja abaixo outras fórmulas de altura do triângulo. As versões simplificadas das equações gerais são mais fáceis de lembrar e calcular.
Como encontrar a altura de um triângulo equilátero
Um triângulo equilátero é um triângulo com todos os três lados iguais e todos os três ângulos iguais a . Todas as três alturas têm o mesmo comprimento, que pode ser calculado a partir de:
- , em que é um lado do triângulo.
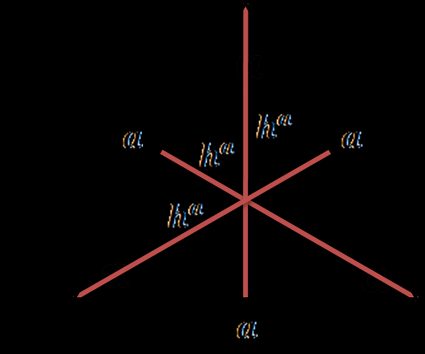
Em um triângulo equilátero, as alturas, as bissetrizes dos ângulos, as bissetrizes das perpendiculares e as medianas coincidem.
Se você estiver interessado nas fórmulas para a área e o perímetro, visite a calculadora de triângulo equilátero, também da Omni.
Como encontrar a altura de um triângulo isósceles
Um triângulo isósceles é um triângulo com dois lados de igual comprimento. Há duas alturas diferentes em um triângulo isósceles. A fórmula para a altura a partir do vértice é:
-
, em que é um dos catetos do triângulo e é sua base. A fórmula é derivada do teorema de Pitágoras. Sobre esse teorema, você pode consultar a nossa calculadora do teorema de Pitágoras.
-
As alturas dos vértices da base podem ser calculadas a partir da:
Fórmula da área:
Trigonometria:
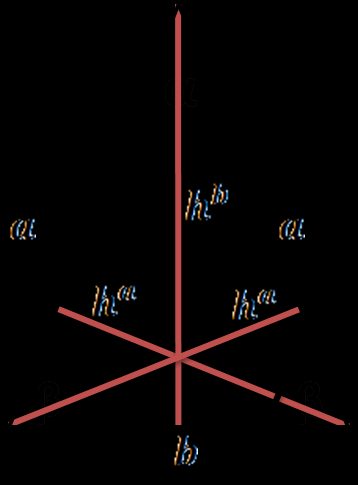
Para obter as fórmulas de área e perímetro desse tipo de triângulo, temos disponível a calculadora de triângulo isósceles.
Como encontrar a altura de um triângulo retângulo
Um triângulo retângulo é um triângulo com um ângulo igual a . Duas alturas são fáceis de encontrar, pois os catetos são perpendiculares: se o cateto menor for a base, o cateto maior será a altura (e vice-versa). A terceira altura de um triângulo pode ser calculada com a fórmula:

Se você estiver interessado nas equações de área e perímetro desse triângulo, consulte a nossa calculadora de triângulo retângulo.
Como encontrar a altura do triângulo com a calculadora da altura de um triângulo da Omni?
Depois de ler nossa explicação, temos certeza de que agora você entende como encontrar a altura de um triângulo sem a área fornecida. Mas vamos ver um exemplo simples para mostrar a flexibilidade da nossa ferramenta:
- Escolha o tipo de triângulo. Suponha que você queira calcular as alturas de um triângulo escaleno, portanto, não alteramos a opção padrão.
- Insira os valores fornecidos. Você pode ter três lados ou dois lados e um ângulo. Vamos ficar com a primeira opção: , , .
- A nossa calculadora exibirá todas as três alturas. Elas são iguais a , e . Além disso, a calculadora nos mostrará todos os ângulos do triângulo, a área e o perímetro.
Incrível, não?
Como encontrar a altura de um triângulo se todos os lados são iguais?
Para determinar a altura de um triângulo equilátero:
- Anote o comprimento do lado de seu triângulo.
- Multiplique-o por
√3 ≈ 1,73. - Divida o resultado por
2. - É isso aí! O resultado é a altura do seu triângulo!
Todas as alturas de um triângulo são iguais?
Em geral, não. Cada altura de um triângulo pode ter um comprimento diferente. Entretanto, se todas as três alturas tiverem comprimentos iguais, então esse triângulo é equilátero, ou seja, todos os seus lados também são iguais (mas não iguais às alturas!).
Como encontrar a altura de um triângulo dados os ângulos?
Você não pode determinar a altura de um triângulo considerando apenas os ângulos do triângulo. Isso ocorre porque há um número infinito de triângulos com esses ângulos e os comprimentos das altitudes em cada um desses triângulos são diferentes!
Como encontrar a altura de um triângulo retângulo?
Cada um dos lados perpendiculares (catetos) em um triângulo retângulo é a sua altura. Para calcular a terceira altura hc, use a fórmula da área:
½ × cateto1 × cateto2 = área = ½ × hipotenusa × hc
Em consequência:
hc = cateto1 × cateto2 / hipotenusa
Qual é a menor altura do triângulo 3 4 5?
A resposta é 2,4. Para chegar a esse resultado, observe que a área é área = ½ × 3 × 4 = 6.
Por outro lado, área = ½ × hipotenusa × altura mais curta.
Como hipotenusa = 5 e área = 6, obtemos altura mais curta = 2 × área / hipotenusa = 2 × 6 / 5 = 2,4.