Calculadora dos Ângulos do Relógio

A calculadora dos ângulos dos relógios da Omni ajudará você a resolver alguns problemas comuns na matemática, como, por exemplo, “Como encontrar o ângulo dos ponteiros do relógio dada uma determinada hora?”

Chegou aquele momento em que você começa a aprender sobre ângulos na escola? Ou talvez você goste de resolver problemas de matemática por diversão e não tem certeza se tem a resposta correta? ⏰

Continue lendo para descobrir:

• Quanto os ponteiros do relógio analógico se movem a cada hora e minuto;
• Como você pode encontrar o ângulo entre os ponteiros do relógio usando apenas o bom senso;
• Como encontrar o ângulo do relógio com fórmulas de ângulos; e
• Por quê você deve sempre visualizar os problemas matemáticos de relógio.

Nossa brilhante calculadora dos ângulos dos relógios ajudará você em todas as suas necessidades. Então, vamos lá! Não temos tempo a perder!

Observe um relógio analógico. O ponteiro das horas, mais curto, dá uma volta completa em 12 horas. Isso significa que a cada hora, ele se move 30 graus.

360° / 12 = 30°

Mas o ponteiro das horas não se move uma vez a cada hora! A cada minuto, ele se move meio grau.

30° / 60 = 0.5°

O ponteiro dos minutos gira completamente em 60 minutos. Portanto, a cada minuto ele se move 6 graus.

360° / 60 = 6°

Para encontrar os ângulos criados pelos ponteiros do relógio, você pode usar dois métodos:

1. O primeiro método é para aqueles que preferem chegar à solução com lógica e sem fórmulas.

2. O segundo método é para aqueles que gostam de usar fórmulas.

Como você sabe, os computadores não têm senso comum, portanto, nossa calculadora dos ângulos dos relógios funciona graças a fórmulas. Como você provavelmente não é um computador, fique à vontade para usar o método com o qual se sente mais confortável.

Encontrar o ângulo entre o ponteiro das horas e o ponteiro dos minutos é fácil quando há uma hora completa em um relógio. O ponteiro dos minutos tem como alvo o número 12, portanto o ângulo é igual à hora multiplicada por 30 graus!

Então, vamos tentar isso em um exemplo:

Exemplo 1: Qual é o ângulo entre os ponteiros de um relógio às 4 horas?

ângulo entre os ponteiros do relógio = 30° ⋅ 4 = 120°

O ângulo que você está procurando é de 120 graus. Mas você sabia que existem dois ângulos entre os ponteiros de um relógio analógico? O segundo preenche o espaço nos outros lados dos ponteiros das horas e dos minutos. Você pode encontrá-lo subtraindo um ângulo de uma volta completa (360°):

360° - 120° = 240°

Nossa calculadora dos ângulos dos relógios dará a você dois ângulos estendidos no sentido horário:

• O ângulo do ponteiro das horas para o ponteiro dos minutos, neste exemplo: 240°; e
• O ângulo do ponteiro dos minutos para o ponteiro das horas, neste caso: 120°.

Agora, vamos ver como você pode encontrar o ângulo entre os ponteiros do relógio sem usar fórmulas em um problema matemático um pouco mais difícil:

Exemplo 2: A hora em um relógio analógico é 10:14. Qual é o ângulo entre os ponteiros do relógio?

Primeiro, desenhe um relógio e marque as partes características do ângulo.

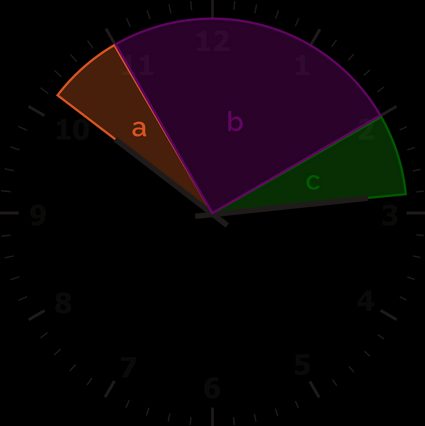
Começamos marcando o ângulo b porque é o mais fácil de encontrar. Ele contém 3 horas inteiras (do número 11 ao número 2), portanto é igual a:

b = 3 ⋅ 30° = 90°

Em seguida, marcamos os dois espaços restantes com a (próximo ao ponteiro das horas) e c (próximo ao ponteiro dos minutos).

Primeiro, vamos encontrar a. Você pode ver na imagem que ele é menor que 30°. A maneira mais fácil de encontrar a é ver a que distância o ponteiro das horas está do número 10. O ângulo entre o ponteiro das horas e o número 10 em um relógio é 14 minutos vezes 0,5°.

14 ⋅ 0.5° = 7°

Então, a que distância o ponteiro das horas está do número 11?

a = 30° - 14 ⋅ 0.5° = 30° - 7° = 23°

Por fim, temos de encontrar o ângulo c. O ponteiro dos minutos se move entre o número dois e onde está agora em quatro minutos. Já sabemos que ele também se move 6° a cada minuto. Portanto, c é igual a:

c = 4 ⋅ 6° = 24°

O ângulo entre o ponteiro das horas e o ponteiro dos minutos é igual a:

ângulo entre os ponteiros do relógio = 90° + 23° + 24° = 137°

Lembre-se: há dois ângulos de relógio! O outro é:

360° - 137° = 223°

Como encontrar o ângulo dos ponteiros do relógio em um exemplo mais difícil?

1. Novamente, comece desenhando um relógio.

2. Marque o ângulo entre o ponteiro dos minutos e as 12 horas. Já sabemos que o ponteiro dos minutos se move 6° a cada minuto. Portanto, para calcular o ângulo entre o ponteiro dos minutos e as 12 horas, multiplique o número de minutos por 6 graus.

   ângulo_mins = 6° × número de minutos

3. Agora, marque o ângulo entre o ponteiro das horas e as 12 horas. Lembre-se de que o ponteiro das horas se move a cada minuto. Portanto, para encontrar o ângulo correto, também precisamos considerar o número de minutos. Portanto, a fórmula do ângulo do relógio para o ponteiro das horas é:

   ângulo_hrs = 30° × número de horas + 0,5° × número de minutos,

   porque o ponteiro das horas se move 30° a cada hora completa e 0,5° a cada minuto.

4. Por fim, encontre dois ângulos do relógio. Para encontrar o primeiro, subtraia o ângulo menor do maior. Em outras palavras, encontre o valor absoluto 🇺🇸 da diferença de dois ângulos:

   primeiro ângulo entre os ponteiros do relógio = |ângulo_hrs - ângulo_mins|

• Como no método anterior, o outro ângulo é elementar (juntos, eles formam um círculo completo):

  segundo ângulo entre os ponteiros do relógio = 360° - primeiro ângulo entre os ponteiros do relógio

Vamos usar essas instruções e resolver um problema matemático de relógio:

Exemplo 3: Encontre o ângulo entre os ponteiros do relógio às 8:23.

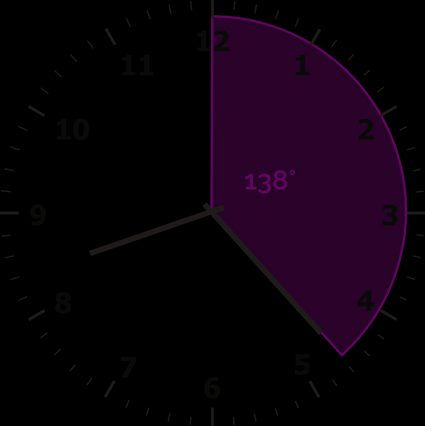
• Primeiro, encontre o ângulo do ponteiro dos minutos. Use a fórmula para o ponteiro dos minutos:

  ângulo_mins = 6° ⋅ 23 = 138°

• Em seguida encontre o ângulo do ponteiro das horas:

  ângulo_hrs = 30° ⋅ 8 + 0,5° ⋅ 23 = 240° + 11,5° = 251,5°

• Por fim, subtraia os valores:

  O ângulo do ponteiro das horas é maior que o ângulo do ponteiro dos minutos, portanto:

  ângulo_hrs - ângulo_mins = 251,5° - 138° = 113,5°.

  O primeiro ângulo entre os ponteiros do relógio é de 113,5°.

• Se necessário, encontre o segundo ângulo:

  360° - primeiro ângulo entre os ponteiros do relógio = 360° - 113,5° = 246,5°

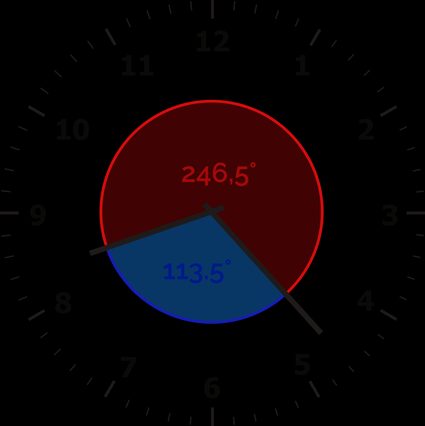
Agora, escolha o método que você mais gosta e resolva todos os seus problemas matemáticos de relógio! E lembre-se: você sempre pode verificar sua resposta na nossa calculadora dos ângulos dos relógios! Antes de ir, no conversor de ângulos 🇺🇸, você pode aprender a converter entre diferentes unidades para descrever ângulos.