Calculadora de Área de Segmento

Use a calculadora de área de segmento da Omni para calcular rapidamente a área de um segmento de circunferência. Você também pode usá-la para encontrar o comprimento de corda e o comprimento do arco. Se você não tiver certeza do que é um segmento de círculo ou mesmo o que é uma corda de círculo, não se sinta constrangido, continue lendo para encontrar algumas definições e imagens autoexplicativas.

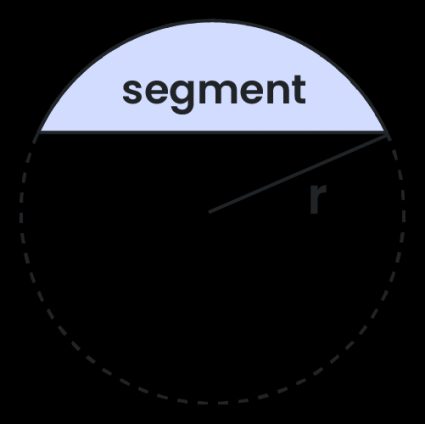
Se você quiser entender o que é o segmento de um círculo, tente imaginar um círculo cortado com um único corte reto. E é isso! Você acabou de criar duas partes do círculo, e a menor delas é chamada de segmento circular. Uma definição matemática mais formal diz o seguinte:

Um segmento circular é uma região delimitada por uma corda e o arco de um círculo (de menos de 180°)

Se for igual a 180°, então, é simplesmente um meio círculo ou semicírculo. De acordo com algumas definições, o ângulo central não precisa ser menor que 180°, nesse caso, você pode dizer que, ao cortar um círculo com uma reta, você obtém dois segmentos: o segmento circular maior e o segmento circular menor.

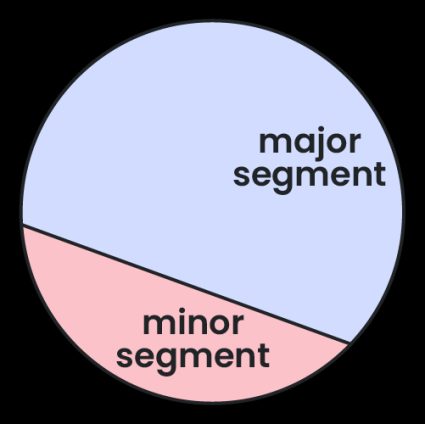
Observe a figura abaixo para ajudar você a visualizar a diferença entre segmento e setor, pois estes dois nomes às vezes são confundidos:

Uma corda é uma reta que conecta dois pontos em um círculo. A extensão infinita da reta de uma corda é chamada de secante. O caso especial de uma corda é aquele que passa pelo centro de um círculo, neste caso, ela é o diâmetro do círculo.

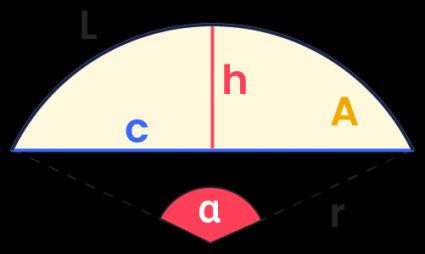
Para encontrar a área do segmento do círculo, você precisa conhecer pelo menos duas variáveis. Em nossa calculadora de área de segmento, você encontrará duas fórmulas populares:

1. Fórmula com o raio e o ângulo central

   A_segmento = 0,5 ⋅ r² ⋅ (α - sen(α))

   De onde vem essa fórmula? Você pode considerar a área do segmento como a diferença entre a área de um setor e a área de um triângulo isósceles formado pelos dois raios:

   A_segmento = A_setor - A_triângulo

   Assim, combinando a fórmula da área do setor:

   A_setor = 0,5 ⋅ r² ⋅ α (saiba mais na calculadora da área do setor circular).

   Com a equação para a área de um triângulo isósceles, dados o raio e o ângulo:

   A_{triângulo isósceles} = 0,5 ⋅ r² ⋅ sen(α) (veja mais detalhes na nossa calculadora de área de triângulos isósceles 🇺🇸).

Obtemos a equação final para a área do segmento de um círculo:

A_segmento = A_setor - A_{triângulo isósceles} = (0,5 ⋅ r² ⋅ α) - (0,5 ⋅ r² ⋅ sen(α)) = 0,5 ⋅ r² ⋅ (α - sen(α))

2. Fórmula dado o raio e a altura

   A_segmento = r² ⋅ arccos((r-h)/r) - (r-h) ⋅ √(2 ⋅ r ⋅ h - h²)

   onde h é a altura de um segmento.

   Essa fórmula pode ter utilidade quando você precisa calcular, por exemplo, o volume de água em um tubo que não está completamente cheio.

Vamos descobrir como você pode usar a calculadora de área de segmento. Em nosso exemplo, queremos encontrar a área da seção transversal de um tubo parcialmente cheio:

1. Insira o raio do círculo. Suponha que o raio do nosso tubo seja de 13 cm.
2. Insira a segunda variável. Digamos que sejam 8 cm de altura do segmento, então, insira este valor no campo altura.
3. E pronto! Agora você sabe que a área de nosso segmento é igual a 138,7 cm². Além disso, determinamos o comprimento da corda (24 cm), o comprimento do arco (30,6 cm) e o ângulo central (134,76°).