Calculadora de Subtração Binária

A calculadora de subtração binária da Omni é uma ótima ferramenta para ajudar você a entender como subtrair números binários. Aqui você pode encontrar descrições dos dois métodos principais que lidam com a subtração de números binários, a saber, o método de empréstimo e o método de complemento. Você também encontrará uma breve nota sobre as diferentes representações de números binários com e sem sinal.

Se você precisar somar números binários, experimente a nossa calculadora de adição binária.

A subtração de números binários é bem similar a dos números decimais, hexadecimais ou qualquer outro sistema de números.

Para esclarecer, os números binários são valores que contêm apenas dois tipos de dígitos, 0 ou 1. Cada dígito se refere às potências de 2 consecutivas e se deve ser multiplicado por 0 ou 1. Como exemplo, 13 em notação decimal é equivalente a 1101 em notação binária, porque 13 = 8 + 4 + 1, ou 13 = 1⋅2³ + 1⋅2² + 0⋅2¹ + 1⋅2⁰ usando notação científica. Use o conversor binário 🇺🇸 da Omni sempre que você precisar alternar entre notação decimal e binária.

Então, como subtrair números binários, por exemplo, 1101 - 110? Sempre podemos converter esses valores em decimais, subtraí-los normalmente e, em seguida, transformá-los novamente na forma binária:

1101₂ - 110₂ = 13₁₀ - 6₁₀ = 7₁₀ = 111₂

Aqui ₂ denota um número binário e ₁₀ é um número decimal. Desde que o número de dígitos seja relativamente pequeno, você pode fazer isso manualmente. Para números longos, isso se torna bastante complicado. E se quisermos subtrair um número maior de um menor? É aqui que a calculadora de subtração binária é útil! Vamos pular para a próxima seção para aprender sobre os diferentes métodos de resolução desses problemas.

Aqui, descreveremos dois métodos para lidar com a subtração de números binários, o método de empréstimo e o método de complemento. Há vários outros truques também, mas esses dois são os mais comuns e ajudam você a entender melhor o problema.

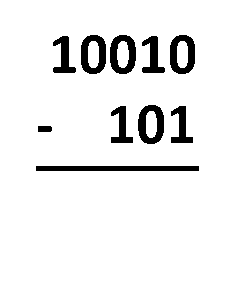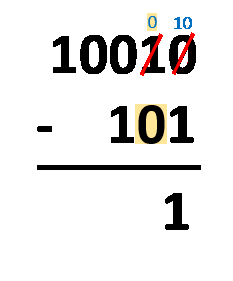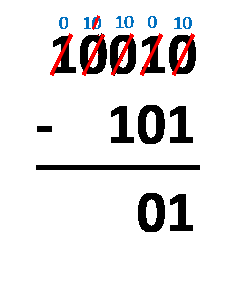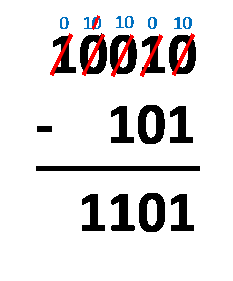
1. No método de empréstimo, tudo o que você precisa fazer é alinhar os números como faria com a subtração decimal normal. O procedimento é quase o mesmo! A única diferença é que você opera com apenas dois números, e não dez. Você precisa subtrair os dígitos na mesma coluna, seguindo estas regras:

   • 1 - 0 = 1;
   • 1 - 1 = 0;
   • 0 - 0 = 0; e
   • 0 - 1 = 1 e "vem -1". Veja que, ao usar essa regra, você deve subtrair -1 do número mais próximo à esquerda, já que você tomou emprestado, ou seja, "vem -1" para o número que você tomou emprestado. Ao fazer isso, o 1 que você tomou emprestado, se torna 0, no fim das contas.

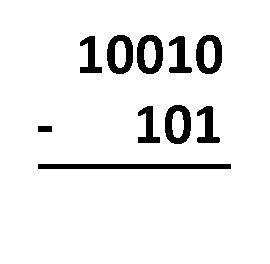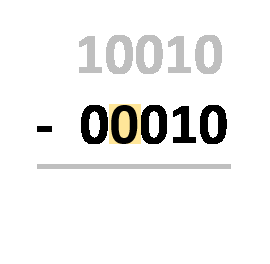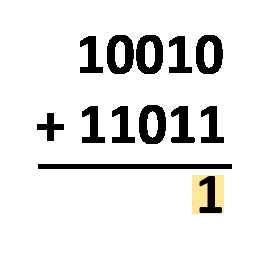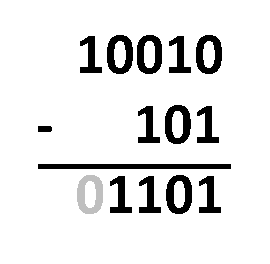
2. No método complementar, o processo consiste em algumas etapas:

   • Alinhe os números como você faria normalmente;
   • Preencha o número de baixo com 0 à esquerda para que ambos os valores tenham o mesmo número de dígitos;
   • Substitua o número de baixo por seu complemento de dois;
   • Some esses dois números binários;
   • Remova o 1 inicial do resultado, pois haverá um dígito a mais do que o necessário; e
   • É isso aí! A parte restante é o resultado final.

Se você quiser ver uma solução passo a passo para o seu problema usando o método do complemento, selecione "Sim" na parte inferior da nossa calculadora de subtração binária. Para obter uma explicação mais detalhada, consulte também nossa calculadora de complemento de dois.

A propósito, você sabia que o conceito de subtração binária é bastante comum em várias ferramentas utilizadas por desenvolvedores? Por exemplo, o comando chmod é uma delas.

Vamos ver como subtrair dois números binários, por exemplo, 110 0101 - 1000 1100. É bastante complicado porque o segundo número tem mais dígitos que o primeiro, portanto, estamos prestes a subtrair um número maior de um menor.

Há uma maneira inteligente de contornar essa tarefa. Podemos usar a identidade a - b = -(b - a), portanto, vamos reverter a ordem da subtração e adicionar um sinal de menos no final. Em outras palavras, estimamos o valor absoluto e, por fim, colocamos um sinal de menos. Vamos usar o método do complemento:

1. Ao inverter a ordem, temos 1000 1100 - 110 0101.

2. Preencha o segundo valor com um zero à esquerda, 1000 1100 - 0110 0101.

3. Encontre o complemento do segundo número, ou seja, troque os dígitos (0→1, 1→0) e some 1, 0110 0101 → 1001 1011.

4. Some o primeiro número e o complemento do segundo juntos, 1000 1100 + 1001 1011 = 1 0010 0111.

5. Remova o 1 inicial e quaisquer 0's adjacentes, 1 0010 0111 → 10 0111.

6. Lembre-se de adicionar um sinal de menos para que o resultado seja -10 0111.

7. O resultado final da subtração desses números binários é 110 0101 - 1000 1100 = -10 0111.

8. Também podemos converter os valores em decimais para confirmar os cálculos: 110 0101₂ - 1000 1100₂ = 101₁₀ - 140₁₀ = -39₁₀ = -10 0111₂. É isso! Chegamos ao resultado correto!

Antes de fazer qualquer cálculo, há um ponto crucial que precisamos levar em conta: a representação dos números em código binário, especialmente o sinal. Explicaremos isso na próxima seção.

Há pelo menos três métodos:

• Use o sinal de menos (-) como fazemos normalmente com números decimais. No código de 8 bits, 5 em binário é 0000 0101, enquanto -5 é -0000 0101.

• Use o primeiro dígito como sinal, normalmente 0 para positivo e 1 para negativo. Agora o -5 se torna 1000 0101.

• Represente um número negativo como o complemento do positivo, portanto, -5 agora é 1111 1011. O primeiro dígito ainda indica o sinal de um número.

Nossa calculadora de subtração binária usa o sinal de menos, ou seja, o primeiro método. Sempre que você copiar um valor para a nossa ferramenta, certifique-se de inserir o número usando a representação apropriada, por exemplo, se ele tiver o primeiro dígito representando o sinal, substitua 1 por - ou deixe 0 como está.

Há pelo menos três métodos que você pode usar para subtrair números binários:

• Método de empréstimo: alinhe os números e subtraia tomando emprestado como sempre, lembrando que 10 - 1 resulta em 1.
• Método do complemento: a ideia é substituir o número subtraído pelo seu complemento e somar os dois números. Lembre-se de omitir o 1 inicial do resultado!
• Método de conversão: converta seus números binários em decimais, subtraia e, em seguida, transforme-os novamente em binários. Eficaz para números pequenos.

Para determinar o complemento de um número binário no sistema de 8 bits, siga estas etapas:

1. Certifique-se de que seu binário tenha 8 dígitos. Se tiver menos, adicione alguns zeros à esquerda.
2. Substitua cada dígito pelo oposto: 0→1 e 1→0.
3. Aumente o número em 1. É isso aí!

101 - 11 = 10. De fato, usando o método de empréstimo, vemos que o último dígito do resultado deve ser 1 - 1 = 0. Então, para realizar 0 - 1, precisamos emprestar 1: 0 - 1 = 10 - 1 = 1. E é isso: como pegamos emprestado, não sobrou nenhum dígito. Portanto, o resultado é 10.