Calculadora da Equação Reduzida da Reta

A calculadora da equação reduzida da reta da Omni ensinará a você como encontrar a equação reduzida de uma reta a partir de quaisquer dois pontos pelos quais essa reta passe. Ela ajudará você a encontrar os coeficientes angular e linear, bem como a interseção entre a reta e os eixos x e y, usando as fórmulas de interseção de inclinação.
Continue lendo para saber o que é a equação reduzida de uma reta, como encontrar a equação de uma reta e a importância da equação reduzida de uma reta na vida real.

Qualquer linha em um plano pode ser descrita matematicamente como uma relação entre as posições vertical (eixo y) e horizontal (eixo x) de cada um dos pontos que contribuem para a linha. Essa relação pode ser escrita como y = [algo que depende de x]. A forma específica de [algo que depende de x] determinará o tipo de linha que temos. Por exemplo, y = x² + x é uma parábola, também chamada de função quadrática. Por outro lado, y = mx + b (com m e b representando quaisquer números reais) é a equação de uma linha reta, na sua forma reduzida.

Nesta calculadora da equação reduzida, vamos nos focar apenas na linha reta. Você pode verificar nossa calculadora de taxa de variação média para encontrar a relação entre as variáveis de funções não lineares.

As equações lineares, ou equações de linha reta, podem ser reconhecidas rapidamente, pois elas não têm termos com expoentes. Por exemplo, você encontrará um x ou um y, mas nunca um x². Cada equação linear descreve uma linha reta, que pode ser expressa na forma da equação reduzida da reta.

Como vimos anteriormente, você pode escrever a equação de qualquer reta na forma de y = mx + b. Essa é a chamada equação reduzida de uma reta, ela fornece a você duas informações importantes: o coeficiente angular m e o coeficiente linear b da linha. Você pode usar esses valores para fazer uma interpolação linear posteriormente.

O termo inclinação se refere ao coeficiente angular, ou gradiente, de uma linha. Ele nos diz o quanto y muda para uma mudança fixa em x. Se for positivo, os valores de y aumentam quando x aumenta. Se for negativo, y diminui com um aumento de x. Você pode ler mais sobre isso na descrição da nossa calculadora de inclinação.

O coeficiente linear se refere ao valor de y no qual a linha cruza o eixo y. Para encontrá-lo, você deve determinar o valor de y para x = 0 na equação. Você verá mais tarde por que o coeficiente linear é um parâmetro importante nas equações lineares e também aprenderá sobre o significado físico de seu valor em determinados exemplos do mundo real.

Você ainda precisa saber como encontrar a interseção da reta com o eixo y? Vamos supor que você conheça dois pontos pelos quais a linha reta passa. O primeiro terá coordenadas (x₁, y₁) e o segundo (x₂, y₂). Suas incógnitas são o coeficiente angular m e o coeficiente linear b.

Em primeiro lugar, substitua as coordenadas dos dois pontos na equação:

1. y₁ = m ⋅ x₁ + b
2. y₂ = m ⋅ x₂ + b

Em seguida, subtraia a primeira equação da segunda:

y₂ - y₁ = m ⋅ (x₂ - x₁)

Por fim, divida os dois lados da equação por (x₂ - x₁) para encontrar o coeficiente angular:

m = (y₂ - y₁)/(x₂ - x₁)

Após encontrar o coeficiente angular, você pode substituí-lo na primeira ou na segunda equação para encontrar a interseção da reta em y:

y₁ = x₁ ⋅ (y₂ - y₁)/(x₂ - x₁) + b

b = y₁ - x₁ ⋅ (y₂ - y₁)/(x₂ - x₁)

A calculadora da equação reduzida da reta da Omni te ajuda a encontrar a equação de uma reta na sua forma reduzida. Tudo o que você precisa fazer é fornecer dois pontos pelos quais a reta passa. Para fazer isso, você precisa seguir o procedimento descrito abaixo.

1. Escreva as coordenadas do primeiro ponto. Vamos supor que seja um ponto com x₁ = 1 e y₁ = 1.

2. Escreva as coordenadas do segundo ponto também. Para o nosso exemplo, suponhamos um ponto com x₂ = 2 e y₂ = 3.

3. Use a fórmula do coeficiente angular para encontrar a inclinação:

   m = (y₂ - y₁)/(x₂ - x₁) = (3-1)/(2-1) = 2/1 = 2.

4. Calcule a interseção da reta em y. Você também pode usar x₂ e y₂ em vez de x₁ e y₁ aqui.

   b = y₁ - m ⋅ x₁ = 1 - 2 ⋅ 1 = -1

5. Junte todos esses valores para construir a forma reduzida da equação da reta:

   y = 2 ⋅ x - 1.

6. Você também pode usar a calculadora de distância para encontrar a distância entre dois pontos.

Também é sempre possível encontrar o ponto de interseção de uma reta com o eixo x. Este é o valor de x no qual a reta cruza o eixo x (significa o valor de x para o qual y é igual a 0). Você pode calculá-lo da seguinte maneira:

0 = m ⋅ x + b

x = -b/m

Como podemos ver, a única condição que deve ser atendida é que o coeficiente angular m seja diferente de zero.

A calculadora da equação reduzida da reta da Omni exibirá os valores da interseção da reta em x e em y para você. Ainda assim, se você quiser saber mais sobre eles, recomendamos que visite a calculadora de interseção em x e em y 🇺🇸 da Omni.

Já vimos o que é a equação reduzida de uma reta, mas para entender porque ela é tão útil, você deve conhecer algumas aplicações que ela tem no mundo real. Vamos ver alguns exemplos. Começaremos com exemplos simples da física para que você possa ter uma ideia intuitiva do que significam a interseção em y e em x.

Imagine um carro movendo-se a uma velocidade fixa em direção a você. Seu movimento pode ser representado como tempo versus a distância que o carro está de você (como mostrado acima). Isso significa que o eixo x representará o tempo passado e o eixo y representará a distância até o carro. Você pode até imaginar que o carro começou a se mover antes de você iniciar o cronômetro (ou seja, antes de t = 0).

Agora, se você observar a interseção em y (x = 0), o ponto em que você começou a controlar o tempo é t = 0. Portanto, o valor de y nesse ponto indicará a posição inicial (distância) do carro em relação a você. Esse valor é, como discutimos anteriormente, equivalente ao coeficiente b na equação reduzida de uma linha reta.

Observando agora a interseção da reta em x (y = 0), esse será o ponto no qual a distância do carro até você será 0. Então, o valor de x nesse ponto será o momento em que você e o carro estavam no mesmo lugar. Esperamos que isso signifique que você estava dentro do carro e não embaixo dele.

O exemplo do carro acima é muito simples e deve ajudar você a entender porque a equação reduzida de uma reta é importante e, mais especificamente, o significado das interseções. Neste artigo, falaremos principalmente sobre linhas retas, mas os pontos de interseção podem ser calculados para qualquer tipo de curva (se ela cruzar um eixo).

De fato, o exemplo acima não se encaixa em uma equação linear e ainda tem ambos os pontos de interseção. O mesmo se aplica a qualquer outra parábola ou outra forma.

Uma equação que tem a garantia de ter uma interseção da reta em y, mas não necessariamente uma interseção da reta em x, é uma parábola. Essa equação é mostrada na imagem acima. Ela tem um máximo ou um mínimo (dependendo da orientação). Se esse máximo estiver abaixo do eixo x ou o mínimo estiver acima do eixo x, nunca haverá uma interseção da reta em x.

Entretanto, nem todas as equações são iguais. Algumas das fórmulas descrevem curvas que talvez nunca interceptem o eixo x, o eixo y ou ambos. Vejamos com um pouco mais de detalhes como isso pode acontecer.

Podemos distinguir 3 grupos de equações, dependendo do fato de elas terem somente uma interseção da reta em y, somente uma interseção da reta em x ou nenhuma. O primeiro grupo (somente interseção da reta em y) pode ser praticamente qualquer tipo de equação, inclusive equações lineares. Um bom exemplo fácil é y = 3 (ou qualquer outro valor constante de y, exceto 0), pois essa é uma linha paralela ao eixo x e, portanto, nunca cruzará ou interseccionará esse eixo. Não tente calcular estes tipos de interseções na calculadora da equação reduzida da reta da Omni. Esses tipos de equações podem potencialmente quebrar a Internet!.

O segundo e o terceiro grupos de equações são um pouco mais complicados de imaginar e, para entendê-los bem, precisamos introduzir o conceito de uma assíntota. Uma assíntota é uma linha (que pode ser expressa como uma equação linear) da qual a função ou curva de que estamos falando se aproxima cada vez mais, mas nunca cruza ou toca essa linha.

A definição pode não parecer totalmente clara, mas se observarmos uma equação de exemplo, teremos menos problemas para entendê-la. Vejamos a equação y = 1/x. Se tentarmos encontrar interseção da reta em y substituindo-a por x = 0, chegaremos ao que é chamado de expressão matematicamente indefinida, pois não faz sentido dividir por 0.

Se tomarmos valores cada vez mais próximos de 0 (algo como 0,1, depois 0,001, 0,000001...), podemos ver que o valor de y aumenta muito rapidamente. Portanto, em torno do ponto x = 0, sabemos que y teria um valor enorme, mas, devido aos fundamentos da matemática, ele não tem um valor definido para esse ponto exato. Às vezes, as pessoas podem dizer 1/0 = ∞, mas a realidade é que infinito não é um número, mas um conceito.

Nesse caso, a equação linear x = 0 representa a assíntota da função y = 1/x, o que significa que y = 1/x nunca interseccionará essa linha e, portanto, não terá um intercepto y. Em geral, toda vez que uma função tem uma assíntota que se encontra em um dos eixos, faltará pelo menos um dos pontos de interseção.

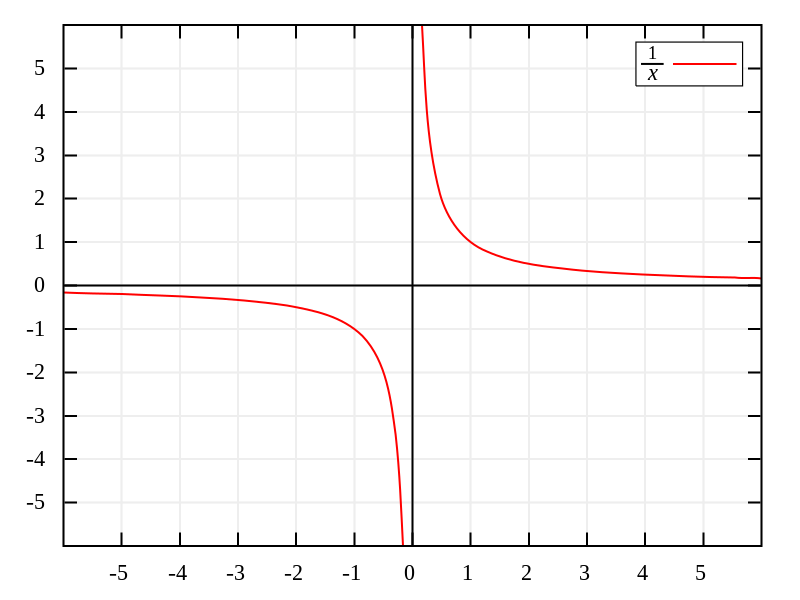
Na verdade, o exemplo que mostramos a você (y = 1/x) também tem uma assíntota para y = 0, ou seja, o eixo x. Pelo mesmo motivo anterior, y = 0 nunca pode ser obtido pela fórmula, pois isso exigiria x = ∞ e, como dissemos antes, é impossível obter isso, pois infinito é um conceito e não um número.

Antes de passarmos para o próximo tópico, é importante observar que fizemos simplificações excessivas ao falar sobre o infinito, mas achamos que é uma abordagem boa e rápida para aqueles que não estão acostumados com o conceito de trabalhar com o infinito em matemática. Recomendamos que você aprenda mais sobre as diferentes formas de infinito, começando com as formas indeterminadas na matemática.

Você poderia facilmente pensar que a utilidade das equações lineares é muito limitada devido à sua simplicidade. Entretanto, a realidade é um pouco diferente. As equações lineares estão no centro de alguns dos métodos mais poderosos para resolver problemas de minimização e otimização.

Os problemas de minimização são um tipo de problema no qual você gostaria de descobrir como tornar uma das variáveis a menor possível. Essa variável pode ser, por exemplo, a diferença entre uma previsão feita por um modelo e a realidade. O processo de minimização é um dos problemas mais comuns encontrados em técnicas de aprendizado de máquina e em experimentos científicos.

Um dos métodos mais comuns e poderosos para encontrar o valor mínimo de uma equação ou fórmula é o chamado método de Newton, que leva o nome do gênio que o inventou. A maneira como ele funciona é usando derivadas, equações lineares e interceptos x:

Esse método consiste em escolher um valor de x para a equação e calcular a derivada da equação nesse ponto. Usando a derivada como a inclinação de uma equação linear que passa por esse ponto exato (x, y), o intercepto x é então calculado. Essa é uma das situações em que a forma de interseção da inclinação é útil.

Depois que a interseção em x é calculada, esse valor de x é usado para repetir o processo acima, um número específico de vezes, até chegarmos a um valor de y que seja mínimo (o que significa que a derivada será 0). Na vida real, não é possível chegar ao ponto mínimo exato em um intervalo de tempo finito, portanto, normalmente, as pessoas se contentam com um valor “suficientemente próximo”.

Um exemplo muito comum é quando você usa o método dos mínimos quadrados para ajustar alguns dados a uma fórmula ou tendência. Nesse caso, o valor que queremos minimizar é a soma da distância ao quadrado da linha de tendência até os pontos de dados, em que a distância é calculada ao longo de uma linha perpendicular do ponto até a linha de tendência.

Não, a forma padrão e a equação reduzida de uma reta são duas maneiras diferentes de descrever uma linha:

• A equação reduzida de uma reta diz: y = m ⋅ x + b, em que m é a inclinação (coeficiente angular) da linha e b é a interseção no eixo y, ou seja, o valor no qual a linha cruza o eixo vertical. Por exemplo, y = -2 ⋅ x + 3.
• A forma padrão é A ⋅ x + B ⋅ y + C = 0, em que A, B, C são inteiros. Por exemplo, 2 ⋅ x + y - 3 = 0.

Se você quiser reescrever sua equação na forma padrão, começando com uma equação reduzida, siga estas etapas:

1. Escreva a forma padrão de sua linha: Ax + By + C = 0.
2. Mova A ⋅ x e C para o lado direito de modo que B ⋅ y permaneça sozinho no lado esquerdo: B ⋅ y = -A ⋅ x - C.
3. Divida ambos os lados por B: y = -(A/B) ⋅ x - (C/B).
4. Como você pode ver, agora temos a equação reduzida da reta y = m ⋅ x + b com inclinação m = -A/B e interseção b = -C/B.

A inclinação (também conhecida como coeficiente angular) descreve a inclinação de uma linha. A inclinação pode ser
positiva, negativa ou zero e:

• A inclinação positiva significa que a linha sobe da esquerda para a direita.
• A inclinação negativa significa que a linha desce da esquerda para a direita.
• O gradiente zero significa que a linha é horizontal.

Quanto maior o valor absoluto do gradiente, mais rápido a linha aumenta/diminui. De fato, o valor da inclinação é exatamente a quantidade pela qual a linha aumenta/diminui quando x aumenta em uma unidade.

A inclinação é m = 1. Para obter esse resultado, use a fórmula m = tan(α), em que α é o ângulo entre a linha e o eixo x. Como tan(45°) = 1, você obtém a inclinação 1, conforme declarado.