Flächeninhalt Rechteck Rechner

Egal, ob du die Fläche eines Teppichs, Pakets, Fernsehbildschirms, rechteckigen Pools oder Fensters berechnen möchtest, dieser Rechner löst dein Problem im Handumdrehen!

Alles, was du tun musst, ist, die Länge und Breite (oder die Diagonale) deines Rechtecks einzugeben und den Rechner die Werte des Umfangs und der Fläche ermitteln lassen.

Lies weiter, wenn du verstehen möchtest, was ein Rechteck ist und dich für die Definition, die Formeln und die Eigenschaften eines Rechtecks interessierst ... Oder wenn du einfach nur wissen möchtest, wie man den Flächeninhalt eines Rechtecks bestimmt.

Ein Rechteck ist ein Viereck mit vier rechten Winkeln. Wir können es auch anders definieren: ein Parallelogramm, das einen rechten Winkel enthält – wenn ein Winkel 90° beträgt, müssen es die anderen auch. Außerdem haben die gegenüberliegenden Seiten eines Rechtecks die gleichen Längen und die benachbarten Seiten sind, im Gegensatz zum Quadrat (Spezialfall des Rechtecks), unterschiedlich lang.

Wenn du dich mit Latein auskennst, erklärt der Name einer Form normalerweise eine Menge. Das Wort Rechteck kommt aus dem Lateinischen rectangulus. Es ist eine Kombination aus rectus (was „senkrecht, gerade” bedeutet) und angulus (ein Winkel) und kann daher auch als einfache, grundlegende Definition eines Rechtecks dienen.

Ein Rechteck ist ein Beispiel für ein Viereck. Verwende unseren Viereck Rechner 🇺🇸, um die Fläche anderer Vierecke zu berechnen.

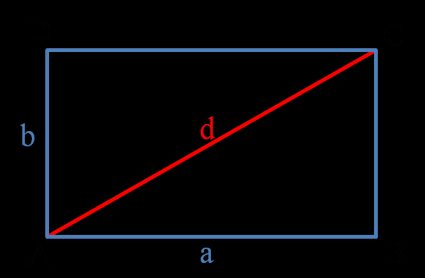
Die obige Abbildung zeigt ein typisches Rechteck. Es hat vier Seiten und vier rechte Winkel. Die Längen der Seiten werden mit a und b bezeichnet, während die Länge der Diagonalen mit d bezeichnet wird.

Wenn alle Seiten des Rechtecks gleich lang sind, wird es Quadrat genannt.

Der Flächeninhalt eines Rechtecks ist der Raum, der durch die Seiten begrenzt wird oder, anders gesagt, der Raum innerhalb des Umfangs eines Rechtecks. Um den Flächeninhalt eines Rechtecks zu bestimmen, musst du nur die Seiten a und b des Rechtecks miteinander multiplizieren:

Flächeninhalt = a × b.

Unser Rechteck-Rechner hat die folgenden Formeln implementiert:

• Für den Flächeninhalt eines Rechtecks:
  A = a × b.

• Für den Umfang eines Rechtecks:
  U = 2 × (a + b) .

• Für die Diagonale eines Rechtecks:
  d² = a² + b² bzw.
  d = √(a² + b²).

Da wir die Formel für die Fläche eines Rechtecks A = a × b kennen, lass uns eine Berechnung anschauen:

1. Wähle die Länge des Rechtecks – zum Beispiel a = 5 cm.
2. Entscheide dich für die Breite des Rechtecks – zum Beispiel b = 6 cm.
3. Multipliziere diese beiden Werte miteinander: A = 5 cm ∙ 6 cm = 30 cm².
4. Der Flächeninhalt des Rechtecks beträgt also 30 cm².

Wir möchten herausfinden, wie man den Umfang eines Rechtecks bestimmt. Er ist die Summe aller Seiten der Form:

U = a + b + a + b

... oder:

U = 2 × (a + b)

Nehmen wir das gleiche Rechteck als Beispiel:

1. Wähle die Länge des Rechtecks – in unserem Fall a = 5 cm.
2. Entscheide dich für die Breite des Rechtecks – z. B. b = 6 cm.
3. Addiere diese beiden Werte: a + b = 5 + 6 = 11 cm.
4. Multipliziere das Ergebnis mit 2: U = 2 ∙ 11 cm = 22 m.
5. Das war's! Der Umfang unseres Rechtecks beträgt 22 cm.

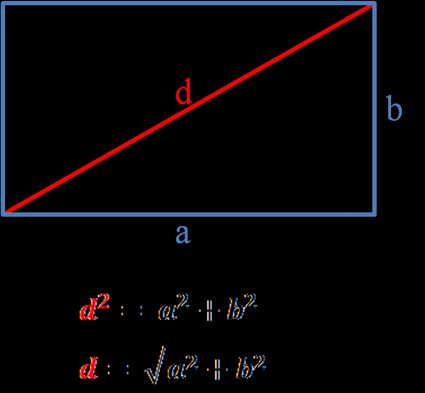
Die Diagonale eines Rechtecks ist ein Segment, das zwei gegenüberliegende Eckpunkte eines Rechtecks miteinander verbindet. Berechnen wir die Länge der Diagonalen des Beispielrechtecks:

1. Wähle die Länge des Rechtecks – zum Beispiel a = 5 cm.
2. Entscheide dich für die Breite des Rechtecks – zum Beispiel b = 6 cm.
3. Quadriere a: a² = 25 cm².
4. Quadriere b: b² = 36 cm².
5. Addiere diese beiden Werte: a² + b² = 25 + 36 = 61 cm².
6. Ziehe schließlich die Quadratwurzel aus dem Ergebnis: d = √(a² + b²) = √61 ≈ 7,81 cm.
7. Die Länge der Diagonalen beträgt also 7,81 cm.

Anstatt all diese Werte schriftlich zu berechnen, kannst du natürlich auch diesen Rechner verwenden. Du kannst ihn auch umgekehrt verwenden – zum Beispiel, um die Breite eines Rechtecks aus einer bekannten Länge und einem bekannten Umfang zu berechnen.

Die Abbildung oben zeigt eine besondere Art von Rechteck, das sogenannte Goldene Rechteck (erfahre darüber mehr mit unserem Goldenes Rechteck Rechner). Ein solches Rechteck erfüllt die folgende Bedingung:

(a + b) / a = a / b = ϕ,

wobei φ der Goldene Schnitt ist, der 1,618 beträgt. Erfahre mehr über diesen besonderen Quotienten mit unserem Goldener Schnitt Rechner.

Wie du auch im Quotientenrechner 🇺🇸 nachlesen kannst, ist ein Verhältnis eine Beziehung zwischen zwei Größen, die oft als Bruch dargestellt wird.

Wusstest du, dass du das goldene Rechteck nur mit einem Lineal und Zirkel konstruieren kannst? Es sind nur ein paar Schritte!

1. Zeichne ein Quadrat.
2. Ziehe eine Linie vom Mittelpunkt der einen Seite des Quadrats zur gegenüberliegenden Ecke. Unser Mittelpunkt Rechner kann dir bei diesem Schritt helfen.
3. Zeichne einen Kreis mit dem Radius dieser Geraden und dem Mittelpunkt, wie in der Abbildung oben.
4. Der Punkt, an dem der Kreis auf die verlängerte Quadratseite trifft, ist die nächste Ecke des goldenen Rechtecks.
5. Finde den letzten Scheitelpunkt und vervollständige das goldene Rechteck.

Taadaaah! Das war doch gar nicht so schwer, oder?

Rechtecke haben viele interessante Eigenschaften, denn sie sind:

• Zyklisch – das bedeutet, dass alle Ecken auf einem einzigen Kreis liegen,
• Gleichwinklig – alle Eckwinkel betragen 90 Grad, und
• Geradlinig – die Seiten treffen sich in rechten Winkeln.
• Sie haben zwei Spiegelsymmetrielinien – senkrecht und waagerecht durch den Mittelpunkt.
• Sie haben zwei Diagonalen, die sich gegenseitig halbieren. Du kannst die Länge der Diagonalen mithilfe des Satzes des Pythagoras ermitteln.
• Die gegenüberliegenden Seiten eines Rechtecks sind parallel zueinander und haben die gleiche Länge.

Was andere, weniger bekannte Eigenschaften des Rechtecks betrifft:

• Der Schnittpunkt der Diagonalen ist der Kreismittelpunkt – es gibt einen Kreis, dessen Mittelpunkt in diesem Punkt liegt und der durch die vier Ecken geht.
• In einem Rechteck mit unterschiedlichen Seitenlängen (einfach gesagt – kein Quadrat) ist es nicht möglich, den Inkreis zu zeichnen.
• Linien, die die Mittelpunkte der Seiten eines Rechtecks verbinden, bilden eine Raute, die die Hälfte der Fläche des Rechtecks ausmacht. Die Seiten der Form sind parallel zu den Diagonalen.

Du kannst dir auch noch weitere Eigenschaften herleiten, z. B. in Bezug auf die Drehung eines Rechtecks – entlang der Seite oder der Diagonalen, um einen Zylinder bzw. einen Kegel zu erhalten.

Kurz gesagt:

1. Ist ein Quadrat ein Rechteck? Ja.
2. Ist ein Rechteck ein Parallelogramm? Ja.
3. Ist ein Rechteck ein Rhombus? Im Allgemeinen – NEIN. Nur, wenn es ein Quadrat ist (die Winkel des Rhombus sind alle 90 Grad).
4. Ist eine Raute ein Rechteck? Im Allgemeinen – NEIN. Nur, wenn sie ein Quadrat ist (die Seiten des Rechtecks sind alle gleich lang).
5. Ist ein Rechteck ein Viereck? Ja, natürlich.
6. Ist ein Rechteck ein Trapez? Ja.

Fragst du dich, ob ein Quadrat ein Rechteck ist oder ein Rechteck ein Parallelogramm? Sieh dir das Bild unten an, und du solltest keine Zweifel mehr an den Beziehungen zwischen Vierecken haben:

Wie kann man dieses Diagramm verstehen? Beginnen wir mit unserem Rechteck. Drei Figuren sind direkt mit der Form verbunden: ein Quadrat, ein Parallelogramm und ein gleichschenkliges Trapez. Wenn also die Form über unserer Form von Interesse liegt – wie Quadrat und Rechteck – können wir sagen, dass:

• jedes Quadrat ein Rechteck ist und ein Quadrat ein Spezialfall eines Rechtecks ist.

Für die anderen beiden Figuren können wir analog dazu sagen:

• Jedes Rechteck ist ein Parallelogramm und ein Rechteck ist ein Sonderfall eines Parallelogramms.
• Jedes Rechteck ist ein Trapez und ein Rechteck ist ein Sonderfall eines Trapezes.

Es gibt viele verschiedene Rankings, in denen Länder bewertet werden – sei es nach Fläche, Bevölkerung, dem Bildungsniveau oder Nobelpreisträgern.

Aber hast du dich schon einmal gefragt, wer den Wettbewerb um das rechteckigste Land gewonnen hat? Der australische Geostatistiker David Barry hat den Parameter der Rechteckigkeit für alle Länder der Welt berechnet und eine Rangliste erstellt.

Er fand heraus, dass das rechteckigste Land Ägypten ist, während der Titel „am wenigsten rechteckiges Land der Welt” an die Malediven geht (der Autor gibt allerdings zu, dass die Berechnungen für Länder, die aus vielen kleinen Inseln bestehen, falsch sein könnten). Schau dir die Tabelle unten an und sieh dir die Top 10 Länder sowie die am wenigsten rechteckigen Länder an.

Ägypten ist der Spitzenreiter, aber das sollte niemanden überraschen, der sich die Form dieses Landes auf der Karte ansieht. Die USA liegen im Mittelfeld der Rangliste, hauptsächlich wegen der Exzentrizität von Alaska und Hawaii. Verwirrend ist, dass das Land mit der zweitgrößten Rechteckigkeit – der Vatikan – gleichzeitig das Land mit der viertgrößten Rundheit ist und Polen, das in der Klassifizierung der Rundheit auf Platz 5 liegt, in der Rangliste der Rechteckigkeit auf Platz 9 liegt.

Wie ist es möglich, das ein Land gleichzeitig rechteckig und rund ist?! Wie du dir denken kannst, dreht sich alles um die Definition von Rechtwinkligkeit und Rundheit, die für komplexe Formen nicht immer angemessen ist – und die Grenzen von Ländern sind in der Regel solche Beispiele, die scharfe Kanten, kleine Inseln oder Kolonien irgendwo auf der anderen Seite des Globus enthalten.

Wenn du dich für das Thema interessierst, kannst du einen Blick auf diese Erklärung und Diskussion der Ergebnisse (englisch) werfen.

Man könnte meinen, dass die Welt leichter zu zeichnen wäre, wenn jedes Land ein Rechteck wäre... Oder nicht?

Die Form eines Rechtecks wird in vielen periodischen Mustern verwendet. Es kann für Wände aus Ziegeln, Bodenfliesen, Pflastern oder verschiedene Mosaike verwendet werden. Im Folgenden findest du einige beliebte Muster:

• Gestapelte Rechtecke – das häufigste und einfachste Fliesenmuster, da die Fliesen in geraden Linien verlegt werden.

• Versetzte Rechtecke typisch für Pflaster-, Fliesen- und Ziegelmuster.

• Fischgrätenmuster – Holzböden sehen mit diesem Muster gut aus.

• Korbgeflecht – wird oft für Flure oder Gehwege im Freien verwendet.

Natürlich gibt es Fliesen in allen Formen und Größen – die Kombination von Sechsecken und Achtecken mit Quadraten ist sehr beliebt. Für das Fünfeck muss die Form unregelmäßig sein, damit ein Fliesenmuster entsteht.

Der Typ Körperform ist eines der meistgesuchten Probleme im Zusammenhang mit Rechtecken. Alles, was du tun musst, ist, die Maße deiner Oberweite, Taille und Hüfte zu messen und die Werte in unseren Rechner entsprechend eingeben. Dann erhältst du die Information, welche Körperform du am ehesten hast.

Bei einer rechteckigen Körperform sind deine Hüfte, Taille und Oberweite ungefähr gleich groß. Dein Körper ist gut proportioniert und sieht athletisch aus.

Wir sind von vielen rechteckigen Objekten umgeben. Deshalb kann unser Rechteck-Rechner nicht nur im Matheunterricht, sondern auch für deine Alltagsprobleme nützlich sein. Natürlich wirst du in der Realität kein ideales Rechteck finden, da es immer eine dritte Dimension hat; aber wenn diese im Vergleich zu den anderen beiden Maßen klein ist, ist es eine sehr gute Annäherung.

• Rechteckige Tischdecken – anhand der Größe deines Tisches kannst du herausfinden, wie groß die Tischdecke sein muss oder wie viel Spitze oder Saumband du verwenden musst.

• Türen oder Fensterglas – hat ein Sturm oder ein Fußball deine Fensterscheibe zerbrochen? Berechne ihre Fläche und schätze die Reparaturkosten anhand des Preises pro Quadratmeter.

• Bildschirme von elektronischen Geräten – Tablets, Smartphones, Fernseher – verwende diesen Rechner für die Fläche eines Rechtecks, um abzuschätzen, wie viel Platz dein Bildschirm an der Wand einnehmen wird – oder wie groß der Bildschirm des Handys ist, das du kaufen möchtest.

• Tafeln, Spiegel, Rahmen, Leinwände, Papierbögen, Notizbücher, Briefumschläge, Geld, Fahnen, rechteckige Pools ... die Liste ist endlos!

Sieh dich um. Kannst du noch mehr rechteckige Gegenstände in deiner Umgebung finden?