Calculadora de fuerza de tensión

Esta calculadora de fuerza de tensión te enseñará a encontrar la fuerza de tensión en una cuerda o cable utilizado para levantar un objeto. Al leer el artículo, también aprenderás a hallar las tensiones en cuerdas utilizadas para tirar de un objeto sobre una superficie sin fricción y verás los diversos diagramas de cuerpo libre para comprender mejor cómo calcular las fuerzas de tensión. Si quieres saber más sobre la tensión y la fórmula de la fuerza de tensión, ¡sigue leyendo!

Imagina que coges un balón de baloncesto del suelo. Sentirías el peso del balón en tus manos debido a la fuerza de gravedad que actúa sobre la masa del balón. Ahora imagina que atas una cuerda alrededor del balón, que luego utilizas para levantarlo de nuevo. Seguirías sintiendo el peso de la pelota a través de la cuerda. En esta situación, la cuerda está ahora en tensión. Lo que mantiene unida la cuerda se llama fuerza de tracción. Si cortas la cuerda, se liberará la fuerza de tensión y la pelota caerá libremente.

La fuerza de tensión es una fuerza axial que atraviesa un objeto que tira, como una cuerda, un cordel, un cable, una cadena… También podemos observar la fuerza de tracción en otros materiales, como varillas y barras, dado que están sometidos a tracciones externas o cargas de tracción. Los materiales con alta resistencia a la tracción son las mejores barras y varillas, ya que no se rompen fácilmente cuando se someten a fuerzas de tracción. Puedes consultar nuestra calculadora de esfuerzos, que trata sobre la elasticidad, para saber más sobre la resistencia a la tracción.

La fuerza de tracción es también un gran ejemplo de la tercera ley del movimiento de Newton. La tercera ley del movimiento de Newton establece que cuando un cuerpo ejerce una fuerza sobre un segundo cuerpo, este ejerce una fuerza igual en sentido contrario sobre el cuerpo original. La fuerza de tracción es una fuerza reactiva que contrarresta una fuerza de tracción externa.

Para calcular la tensión que actúa en una cuerda, primero tenemos que entender la segunda ley del movimiento de Newton. La segunda ley del movimiento de Newton establece que la suma de las fuerzas que actúan sobre un objeto de masa constante es igual a la masa de ese objeto multiplicada por su aceleración. También podemos expresar esta afirmación como una ecuación:

ΣF = m × a

donde:

• Σ (sigma) denota la suma de fuerzas F.
• m es la masa del objeto.
• a es la aceleración.

Para un objeto suspendido por una cuerda, podemos utilizar la aceleración debida a la gravedad 🇺🇸, g, como su aceleración. La aceleración gravitatoria nos da el valor de su peso en términos de fuerza, como en Newtons o libra-fuerza. Si el objeto se mueve con una aceleración distinta, debemos utilizar su aceleración real para el cálculo. Sin embargo, esta calculadora de tensión sólo determina las fuerzas de tensión en casos de equilibrio estático.

Esta afirmación significa que esta herramienta sólo considera objetos en reposo en un sistema dado. En la calculadora de fuerza de tensión, también suponemos que las cuerdas no tienen masa y, por tanto, no contribuyen en nada a las fuerzas de tensión. También suponemos que las masas u objetos están en el vacío y no experimentan fricción ni resistencia del aire hacia su entorno.

Podemos ver en la ilustración siguiente que la fuerza, F, necesaria para levantar el objeto es igual al peso, W (del inglés weight), del objeto. Esta idea es el concepto fundamental en el que se basa nuestra fórmula de la fuerza de tracción. También se muestra a continuación el diagrama de cuerpo libre del objeto, que muestra las fuerzas de tensión, T, que actúan en la cuerda. Como puedes ver, las fuerzas de tensión actúan por pares y en sentidos opuestos:

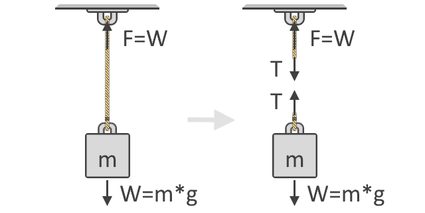
Siguiendo la segunda ley del movimiento de Newton, podemos expresar la suma de fuerzas utilizando el diagrama de cuerpo libre del objeto, como se muestra a la derecha de la ilustración anterior. Utilizamos los diagramas de cuerpo libre para mostrar las distintas direcciones y magnitudes de las fuerzas que actúan sobre un cuerpo. En equilibrio, todas estas fuerzas deben ser iguales a cero. Considerando todas las fuerzas hacia arriba como positivas y hacia abajo como negativas, nuestra ecuación es:

ΣF↑ = 0 = T + (-W)

T = W

donde el peso, W, pasa a ser negativo, ya que está dirigido hacia abajo. Transponiendo W al otro lado de la ecuación, podemos ver ahora que la fuerza de tracción de la cuerda es igual al peso del objeto que transporta, como también se ha mostrado anteriormente.

Si utilizamos más cuerdas para levantar el objeto, la fuerza de tensión total se divide entre las cuerdas. La fuerza de tracción en cada cuerda depende de su ángulo respecto a la dirección de la fuerza a la que se opone. Para comprenderlo mejor, consideremos otro diagrama de cuerpo libre de un objeto suspendido por dos cuerdas, como se muestra a continuación:

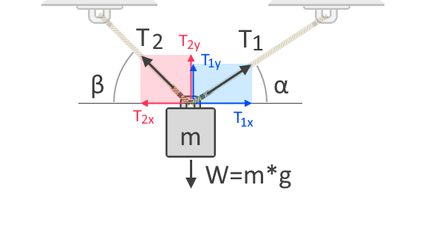
En el diagrama de cuerpo libre mostrado arriba, podemos ver las componentes horizontal y vertical de las fuerzas de tracción, T₁ y T₂. Las fuerzas son vectores, lo que significa que siempre tienen magnitudes y direcciones. Como todos los vectores, las fuerzas pueden expresarse en estas componentes, que dan la influencia de la fuerza a lo largo de los ejes horizontal y vertical. T₁ₓ y T₂ₓ son las componentes verticales de T₁ y T₂, respectivamente. Por otro lado, T_1y y T_2y son las componentes verticales de las mismas fuerzas, respectivamente. Como la gravedad actúa sobre el objeto en el eje vertical, debemos considerar las componentes verticales de las fuerzas de tracción para nuestra suma de fuerzas de la siguiente manera:

ΣF↑ = 0 = T_1y + T_2y + (-W)

W = T_1y + T_2y

Como también conocemos los ángulos de las fuerzas de tracción, podemos expresar T_1y y T_2y en términos de T₁ y T₂, respectivamente, con ayuda de funciones trigonométricas:

T_1y = T₁ × sen(α)

T_2y = T₂ × sen(β)

W = T₁ × sen(α) + T₂ × sen(β)

También podemos decir que para que el sistema esté en equilibrio, el objeto no debe moverse horizontalmente ni a lo largo del eje x. Por tanto, las componentes horizontales de T₁ y T₂ deben ser iguales a cero. Además, con ayuda de la trigonometría, podemos expresar T₁ₓ y T₂ₓ en términos de T₁ y T₂, respectivamente:

T₁ₓ = T₂ₓ

T₁ × cos(α) = T₂ × cos(β)

Si dividimos ambos lados por cos(α), obtenemos una ecuación en la que T₁ se expresa en términos de T₂ y de los ángulos:

T₁ = T₂ × cos(β) / cos(α)

Podemos utilizar esta ecuación para resolver T₂ sustituyendo T₂ × cos(β) / cos(α) por T₁ en nuestra ecuación de suma de fuerzas, como se muestra a continuación:

W = T₁ × sen(α) + T₂ × sen(β)

W = T₂ × [cos(β) / cos(α)] × sen(α) + T₂ × sen(β)

W = T₂ × [cos(β) × sen(α) / cos(α) + sen(β)]

T₂ = W / [cos(β) × sen(α) / cos(α) + sen(β)]

Por último, si multiplicamos toda esta ecuación por cos(β) / cos(α), tal como derivamos en el valor de T₁ en términos de T₂, y luego lo simplificamos todo, obtenemos esta ecuación:

T₁ = W / [cos(β) × sen(α) / cos(α) + sen(β)] × [cos(β) / cos(α)]

T₁ = W / [cos(β) × sen(α) / cos(α) + sen(β)] × [cos(β) / cos(α)]

T₁ = W / [cos(α) × sen(β) / cos(β) + sen(α)]

Ahora sólo necesitas conocer los ángulos de las cuerdas de tracción con respecto a la horizontal. Si te dan un ángulo con respecto a la vertical, sólo tienes que restar este ángulo de 90°. Así obtendrás el ángulo respecto a la horizontal. Sin embargo, si te dan otros valores de ángulos que pueden ser mayores de 90° o incluso de 180°, puedes consultar nuestra calculadora del ángulo de referencia para que te ayude a determinar el ángulo que necesitas. Tras determinar los valores de las variables en nuestras fórmulas de fuerza de tracción, ahora podemos resolver las fuerzas de tracción propiamente dichas.

La forma de hallar la fuerza de tracción sobre un objeto del que se tira es igual que cuando el objeto está colgado. La única diferencia es que primero tenemos que calcular la aceleración de todo el sistema y sumar todas las fuerzas a lo largo de la horizontal. Si la cuerda está inclinada respecto al nivel del piso, debemos calcular también la componente horizontal de la fuerza de tracción.

Veamos el siguiente ejemplo para comprender mejor cómo hallar la fuerza de tracción en una cuerda que tira de uno o dos objetos. En este ejemplo, dos objetos son arrastrados por una única fuerza de tracción aplicada. Otra cuerda tira del segundo objeto, que está unido al primero, como se muestra a continuación:

Esta ilustración muestra que las masas de m₁ y m₂ son 3 kg y 2 kg, respectivamente. La suma de estas dos masas da la masa total del sistema, 5 kg. También tenemos que determinar la componente horizontal de la fuerza de tracción, T = 24 N, que está en un ángulo θ = 60°. Si volvemos a utilizar las funciones trigonométricas, podemos decir que la componente horizontal de la fuerza de tracción es igual a 24 N × cos(60°), lo que equivale a 12 N. Ahora que conocemos la componente horizontal de la fuerza de tracción y la masa total del sistema, podemos calcular la aceleración, a, del sistema de la siguiente manera:

F = m × a → a = F / m

a = 12 N / 5 kg = 2.4 m/s²

Una vez hallada la aceleración del sistema, podemos volver a utilizar la segunda ley del movimiento de Newton para calcular la tensión de la cuerda o cable del sistema. Para ello, multiplica la aceleración por la masa de la que tira la cuerda. Para T₂, su diagrama de cuerpo libre nos muestra que sólo es responsable de la masa de m₂; podemos decir que T₂ = a × m₂. Dicho esto, T₂ = (2.4 m/s²) × (2 kg) = 4.8 N. Por otro lado, T₁ es la fuerza de tracción que tira tanto del peso de m₁ como de m₂. Sin embargo, ya tenemos el valor de T₁, que es simplemente igual a T = 24.0 N. Por tanto, T₁ = 24.0 N.

En nuestro ejemplo, si las cuerdas izquierda y derecha fueran una sola cuerda, podríamos comparar este montaje con un sistema de poleas. Una polea es una máquina sencilla que aprovecha las fuerzas de tensión de las cuerdas para obtener una ventaja mecánica. Puedes consultar nuestra calculadora de poleas 🇺🇸 y nuestra calculadora de longitud de correas (que es un sistema de dos poleas) para saber más sobre la relación de transmisión y la tensión.