Calculadora del ángulo de referencia

Nuestra calculadora de ángulos de referencia es una herramienta que te permite recalcular ángulos a su versión correspondiente en el primer cuadrante. Todo lo que tienes que hacer es introducir cualquier ángulo positivo y la calculadora encontrará el ángulo de referencia por ti. En este artículo se explica qué es un ángulo de referencia y se proporciona una definición de ángulo de referencia.

También se brinda una guía paso a paso sobre cómo encontrar un ángulo de referencia en radianes y grados, junto con algunos ejemplos. Sigue leyendo y también encontrarás la gráfica de los cuadrantes.

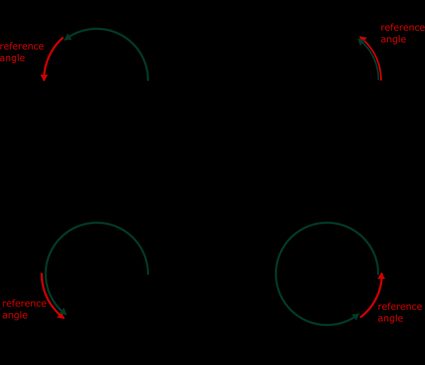
Fíjate en la imagen anterior. Todo ángulo se mide desde la parte positiva del eje x hasta su lado terminal (la línea que determina el extremo del ángulo) yendo en sentido contrario a las agujas del reloj. Si quieres encontrar el ángulo de referencia, debes buscar el ángulo más pequeño que se forma entre el eje x y el lado terminal, ya sea en sentido horario o antihorario.

Los ángulos de referencia son útiles en trigonometría. Por ejemplo, si quieres hallar el seno o el coseno de cualquier ángulo, primero debes buscar su ángulo de referencia en el primer cuadrante. Luego puedes encontrar la función trigonométrica del ángulo de referencia y elegir el signo adecuado.

En la tabla siguiente encontrarás los ángulos más utilizados y sus funciones trigonométricas:

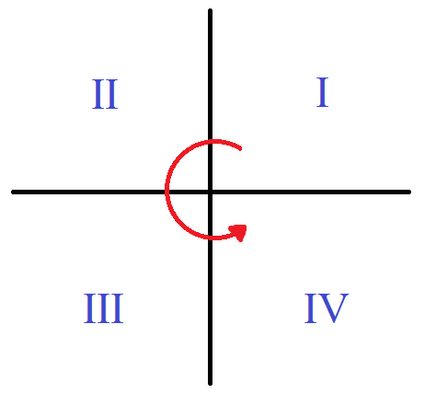
Los dos ejes de un sistema cartesiano 2D dividen al plano en cuatro regiones infinitas llamadas cuadrantes. La numeración comienza en el cuadrante superior derecho, donde ambas coordenadas son positivas, y continúa en dirección antihoraria, como se muestra en la imagen.

Generalmente, las funciones trigonométricas (seno, coseno, tangente, cotangente) dan el mismo valor tanto para un ángulo como para su ángulo de referencia. Lo único que cambia es el signo: estas funciones son positivas y negativas en varios cuadrantes. Sigue la regla nemotécnica “todos saben que Tania corre” (TSTC) para recordar cuándo estas funciones son positivas.

• T para todas: en el primer cuadrante, todas las funciones trigonométricas tienen valores positivos.
• S para seno: en el segundo cuadrante, solo la función seno tiene valores positivos.
• T(an) para tangente: en el tercer cuadrante, la tangente y la cotangente tienen valores positivos.
• C para coseno: en el cuarto cuadrante, solo la función coseno tiene valores positivos.

Si no te gusta esta regla, aquí tienes otras nemotécnicas que puedes utilizar:

• todas las sopas tienen caldo 🍲;
• todos saltan tanques confiados 🦘;
• todos sabemos tantos caminos 🌏; o
• todos los sabuesos terminan en el cielo 🐶.

Asegúrate de echar un vistazo a nuestra calculadora del teorema del coseno 🇺🇸 y nuestra calculadora del teorema del seno para obtener más información sobre trigonometría.

Solo tienes que seguir estos pasos:

1. Elige tu ángulo inicial: por ejemplo, 610°.

2. Si tu ángulo es mayor que 360° (un ángulo completo), resta 360°. Sigue haciéndolo hasta que obtengas un ángulo menor que un ángulo completo. Esto es lo mismo que hallar el módulo. En este ejemplo, tras restar 360°, obtenemos 250°.

3. Determina en qué cuadrante se encuentra tu ángulo:

   • de 0° a 90° — primer cuadrante,
   • 90° a 180° — segundo cuadrante,
   • 180° a 270° — tercer cuadrante,
   • 270° a 360° — cuarto cuadrante.

   En este caso, 250° se encuentra en el tercer cuadrante.

4. Elige la fórmula adecuada para calcular el ángulo de referencia:

   • de 0° a 90°: ángulo de referencia = ángulo,
   • de 90° a 180°: ángulo de referencia = 180° - ángulo,
   • de 180° a 270°: ángulo de referencia = ángulo - 180°,
   • de 270° a 360°: ángulo de referencia = 360° - ángulo.

   En este caso, tenemos que elegir la fórmula ángulo de referencia = ángulo - 180°.

5. Sustituye tu ángulo en la ecuación para hallar el ángulo de referencia:

   ángulo de referencia = 250° - 180° = 70°.

Si necesitas una herramienta que te ayude a convertir entre distintas unidades de medida de ángulos, prueba nuestra conversión de ángulos 🇺🇸.

¡Es más fácil de lo que parece!

1. Para ángulos mayores de 2π, resta múltiplos de 2π hasta obtener un valor menor que un ángulo completo.

2. Determina los cuadrantes:

• 0 a π/2 — primer cuadrante, por lo que ángulo de referencia = ángulo.
• π/2 a π — segundo cuadrante, por lo que ángulo de referencia = π - ángulo.
• π a 3π/2 — tercer cuadrante, por lo que ángulo de referencia = ángulo - π.
• 3π/2 a 2π — cuarto cuadrante, por lo que ángulo de referencia = 2π - ángulo.

Como puedes ver, este procedimiento es similar al anterior para ángulos en grados. Como ejemplo, consideremos el ángulo de 28π/9 radianes.

1. Habiendo restado los múltiplos de 2π, nos queda 10π/9.

2. 10π/9 es un poco más grande que π, por lo que se encuentra en el tercer cuadrante. El ángulo de referencia es:

   ángulo de referencia = ángulo - π = π/9.

Solo debes seguir estos pasos:

1. Escribe el ángulo en la casilla. Puede ser cualquier ángulo positivo que imagines; digamos que queremos encontrar el ángulo de referencia de 210°. Si lo deseas, también puedes cambiar las unidades, por ejemplo, a radianes.

2. ¡Eso es todo! La calculadora del ángulo de referencia encontrará la versión aguda de tu ángulo, así como el cuadrante en el que se encuentra el ángulo original. En nuestro caso es de 30°, y el ángulo inicial se encuentra en el tercer cuadrante.

Si quieres una respuesta rápida, echa un vistazo a la siguiente lista:

Primer cuadrante:

Segundo cuadrante:

Tercer cuadrante:

Cuarto cuadrante: