Calculadora de triángulos notables 30-60-90

Con esta calculadora de triángulos notables 30-60-90, puedes resolver las medidas de este tipo de triángulo rectángulo. Tanto si buscas las fórmulas para la hipotenusa del triángulo 30-60-90, como si te preguntas cuáles son las proporciones del triángulo rectangulo de 30-60-90, o simplemente quieres comprobar cómo es ese triángulo, has llegado al sitio adecuado.

Sigue leyendo para obtener más información sobre este triángulo rectángulo en concreto, o echa un vistazo a la herramienta hecha para su hermano gemelo: calculadora de triángulos 45-45-90.

Antes de investigar esta calculadora de triángulos notables de 30, 60 y 90, expliquemos qué significa "30-60-90". Un triángulo notable es un triángulo con propiedades especiales Cuando hablamos del triángulo rectángulo de 30-60-90, nos referimos a los ángulos del triángulo, que son iguales a 30°, 60° y, obviamente, 90°.

Este triángulo a veces se abrevia como "triángulo de 30 y 60" puesto que el tercer ángulo sólo puede medir 90° y, por lo tanto, se puede omitir del nombre. Además este triángulo especial, o notable, es fácil de resolver con el teorema de 30° o teorema de 60° que permiten obtener funciones trigonométricas de estos ángulos y sus relaciones fácilmente.

Supongamos que el cateto más corto de un triángulo notable 30-60-90 es igual a a. Entonces:

• El segundo cateto es igual a a√3;
• La hipotenusa es 2a;
• El área es igual a a²√3/2; y
• El perímetro es igual a a(3 + √3).

Las fórmulas del triángulo rectángulo de 30 y 60 son bastante fáciles, pero ¿cuál es la matemática detrás de ellas? Veamos qué métodos puedes utilizar para demostrarlas:

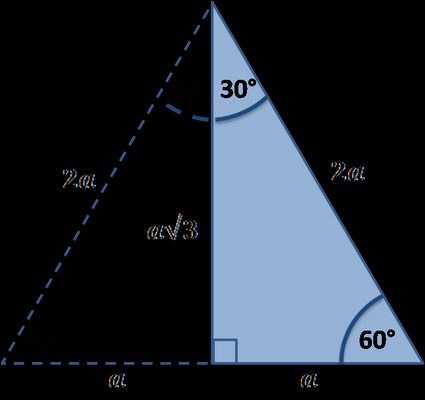
1. Usar las propiedades del triángulo equilátero

   ¿Te has dado cuenta de que nuestro triángulo de interés es simplemente la mitad del triángulo equilátero? Si recuerdas la fórmula para la altura de ese triángulo regular, tienes la respuesta a cuál es la longitud del segundo cateto. Es igual al lado por la raíz cuadrada de 3, dividido por 2:

   h = c√3/2, h = b y c = 2a, por lo que b = c√3/2 = a√3

2. Usar trigonometría

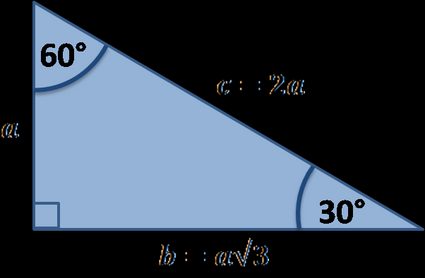
Si estás familiarizado con los fundamentos trigonométricos, puedes utilizar, por ejemplo, el teorema de 30°, es decir, el seno y el coseno de 30° para averiguar las longitudes de los otros lados:

a/c = sen(30°) = 1/2, así que c = 2a

b/c = sen(60°) = √3/2 por lo que b = c√3/2 = a√3

Además, si conoces dos lados del triángulo, puedes hallar el tercero a partir del teorema de Pitágoras. Sin embargo, los métodos descritos anteriormente son más útiles, ya que solo necesitan la medida de un lado del triángulo (siempre y cuando sea del tipo 30-60-90).

Veamos cómo las fórmulas y teoremas usados en esta calculadora de triángulos notables de 30, 60 y 90.

Si conocemos la longitud del cateto más corto a, entonces:

• b = a√3

• c = 2a

Si el único parámetro dado es la longitud del cateto más largo, b, entonces:

• a = b√3/3

• c = 2b√3/3

Conocida la hipotenusa c, las fórmulas de los catetos quedan como sigue:

• a = c/2

• b = c√3/2

O simplemente escribe los valores dados en la calculadora de triángulos 30-60-90 y esta hará el resto.

La regla más importante que hay que recordar es que este triángulo rectángulo especial tiene un ángulo recto (de ahí que se llame triángulo de 30, 60 y 90), y sus lados poseen una proporción coherente y fácil de recordar, la cual es a : a√3 : 2a. Además, la inusual propiedad de un triángulo 30-60-90 es que es el único triángulo rectángulo con ángulos en progresión aritmética.

¿Qué es una progresión aritmética? Consulta nuestra calculadora de progresiones aritméticas para saber más.

En todos los triángulos de 30 y 60 (que son los triángulos que calculamos con esta calculadora de triángulos de 30, 60 y 90) las proporciones son:

• 1 : 2 : 3 para los ángulos (30° : 60° : 90°);
• 1 : √3 : 2 para los lados (a : a√3 : 2a).

Ya conoces las reglas de un triángulo rectángulo de 30 y 60. Es hora de practicar.

1. Introduce el valor dado. Supongamos que queremos ver cómo resolver el triángulo 30-60-90 del juego de escuadras mencionado antes. Hay una escala en el cateto más largo. Supongamos que su longitud es de b = 32 centímetros.
2. Ingresa el valor de b en la calculadora, ¡y aparecen todos los demás valores! Gracias a esta calculadora de triángulos 30-60-90, puedes encontrar que:

• El cateto más corto mide 18.48 cm, porque a = b√3/3 = 32 cm × √3/3 ≈ 18.48 cm.
• La hipotenusa es igual a 36.95 cm, porque c = 2b√3/3 = 2a ≈ 36.95 cm.
• El área es 295.6 cm², y resulta de multiplicar la longitud de los catetos y dividir por 2: área = (a²√3)/2 ≈ 295.6 cm².
• El perímetro es igual a 87.4 cm, la suma de todos los lados da ese resultado Perímetro = a + a√3 + 2a = a(3 + √3) ≈ 87.4 cm.