Calculateur de cosinus
Ce calculateur de cosinus est un outil similaire à notre calculateur de sinus 🇺🇸. Rajoutez le calculateur de tangente 🇺🇸, et vous n'aurez plus de problèmes avec les fonctions trigonométriques 🇺🇸 les plus utilisées. Il suffit de saisir l'angle, exprimé en degrés ou en radians, et vous trouverez la valeur du cosinus en un clin d'œil.
Continuez votre lecture ! Dans cet article, vous trouverez la définition de cosinus, qui vous aidera à comprendre ce qu'est la fonction cosinus. Puis, vous apprendrez comment calculer le cosinus d'un angle.
Nous avons également préparé un tableau des valeurs du cosinus des angles plus connus : cos 0°, cos 30° ou cos 45°, entre autres.
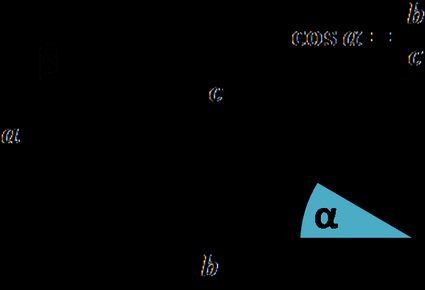
Définition de cosinus : qu'est-ce le cosinus et comment calculer le cosinus d'un angle ?
Le cosinus est l'une des fonctions trigonométriques de base. Tout comme le sinus, le cosinus peut être défini à l'aide d'un triangle rectangle ou du cercle unité.
Le cosinus d'un angle est égal à la longueur du côté adjacent à l'angle en question divisée par la longueur de l'hypoténuse.
Comment calculer le cosinus de cet angle, vous demandez-vous ?
cos(α) = coté adjacent à α / hypoténuse = b / c
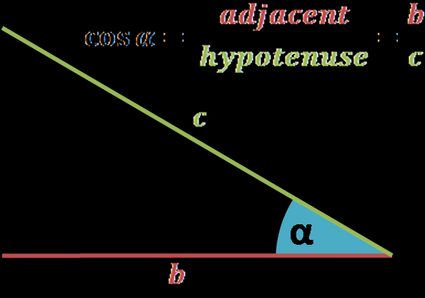
Si vous ne connaissez pas les notions du côté adjacent, du côté opposé ou de l'hypoténuse, consultez le calculateur de sinus (lien au début de cet article).
Le terme « cosinus » vient de la fonction sinus avec le préfixe latin co-, et littéralement, il signifie complément du sinus. Et, en effet, la fonction cosinus peut être définie de cette façon, car c'est le sinus de l'autre angle aigu. L'abréviation de cosinus est cos, par exemple cos(30°).
Voici des propriétés importantes de la fonction cosinus.
- Le cosinus est toujours compris entre -1 et 1 : -1 ≤ cos(α) ≤ 1.
- La période du cosinus est égale à 2π.
- Il s'agit d'une fonction paire (alors que le sinus est impair), ce qui veut dire que cos(-α) = cos(α).
- La définition du cosinus est essentielle pour comprendre la loi des cosinus – une loi très utile pour trouver les paramètres de tous les triangles. Découvrez-la avec notre calculateur de la loi des cosinus 🇺🇸 !
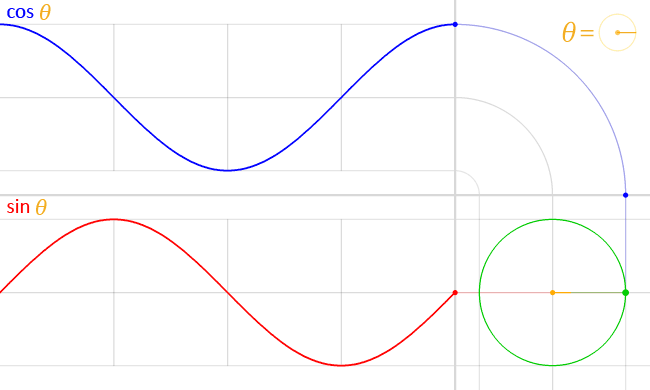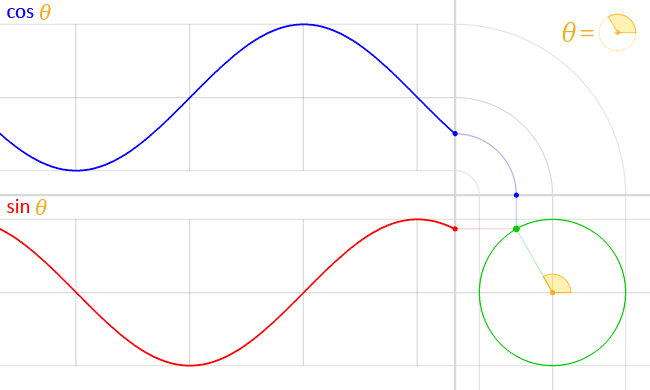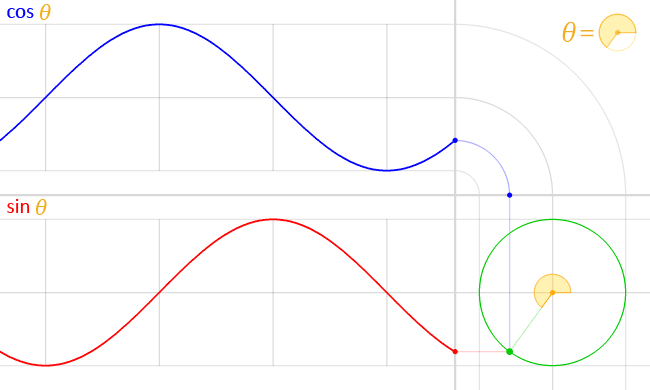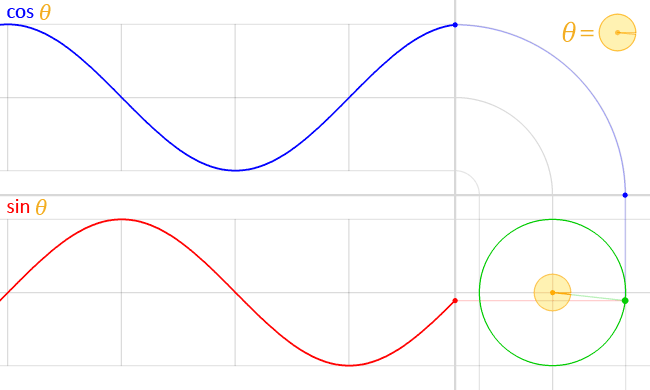
Graphique et tableau des cosinus : cos 0°, cos 30°, cos 45°, etc.
L'image ci-dessous montre la fonction cosinus entre -2π et 2π. Si vous souhaitez apprendre à jouer avec cette fonction, assurez-vous de consulter le calculateur de déphasage 🇺🇸.
La valeur exacte du cosinus est particulièrement facile à retenir et à définir pour certains angles. Vous avez probablement appris que cos 0° = 1, cos 30° = √3/2 et cos 45° = √2/2. D'autres angles de base sont indiqués dans le tableau ci-dessous.
Votre angle n'est peut-être pas inclus, mais ne vous inquiétez pas ! Souvenez-vous comment calculer le cosinus d'un angle en consultant l'explication que nous avons vue tout à l'heure, ou utilisez le calculateur de cosinus.
α (angle) | sin(α) | ||
|---|---|---|---|
Degrés | Radians | Exact | Décimal |
0° | 0 | 1 | 1 |
15° | π/12 | (√6 + √2) / 4 | 0,965 925 826 3 |
30° | π/6 | √3/2 | 0,866 025 403 8 |
45° | π/4 | √2/2 | 0,707 106 781 2 |
60° | π/3 | 0,5 | 0,5 |
75° | 5π/12 | (√6 − √2) / 4 | 0,258 819 045 1 |
90° | π/2 | 0 | 0 |
105° | 7π/12 | -(√6 − √2) / 4 | -0,258 819 045 1 |
120° | 2π/3 | -0,5 | -0,5 |
135° | 3π/4 | -√2/2 | -0,707 106 781 2 |
150° | 5π/6 | -√3/2 | -0,866 025 403 8 |
165° | 11π/12 | -(√6 + √2) / 4 | -0,965 925 826 3 |
180° | π | -1 | -1 |
Par ailleurs, vous pouvez observer comment la fonction cosinus se comporte dans les différents quadrants. Rappelez-vous la périodicité de la fonction cosinus cos(α + 360°) = cos(α) si votre angle ne figure pas dans le tableau ci-dessous.
Quadrant | Degrés | Radians | Valeur | Signe | Tendance | Convexité |
|---|---|---|---|---|---|---|
0° | 0 | 1 | Maximum | |||
1er quadrant | 0° < α < 90° | 0 < α < π/2 | 0 < cos(α) < 1 | + | Décroissant | Concave |
90° | π/2 | 0 | Inflexion | |||
2e quadrant | 90° < α < 180° | π/2 < α < π | -1 < cos(α) < 0 | - | Décroissant | Convexe |
180° | π | -1 | Minimum | |||
3e quadrant | 180° < α < 270° | π < α < 3π/2 | -1 < sin(α) < 0 | - | Croissant | Convexe |
270° | 3π/2 | 0 | Inflexion | |||
4e quadrant | 270° < α < 360° | 3π/2 < α < 2π | 0 < sin(α) < 1 | + | Croissant | Concave |
Exemple : comment utiliser le calculateur de cosinus ?
Maintenant que vous savez ce qu'est la fonction cosinus, utiliser ce calculateur de cosinus sera un jeu d'enfant !
-
Saisissez l'angle. Cliquez sur l'unité pour passer des degrés en radians et vice versa. Prenons, par exemple, un angle de 40°.
-
Restez calme et lisez le résultat. Ici, nous voyons que cos(40°) ≈ 0,766.
Rappelez-vous qu'il s'agit d'une valeur approximative. Dans certains cas, il est impossible de trouver la solution exacte.
Essayez ce calculateur de cosinus ! Vous pouvez même insérer la valeur du cosinus pour trouver l'angle. Une seule chose à tenir à l'esprit : notre calculateur ne supporte que des angles compris entre 0 et 180°. Mais vous connaissez la périodicité du cosinus, vous êtes conscient⋅e que c'est une fonction paire, et vous savez comment calculer le cosinus d'un angle. Vous n'aurez pas de problèmes à trouver d'autres solutions possibles.