Calculateur de hauteur d'un triangle

Ce calculateur de hauteur d'un triangle est l'outil qu'il vous faut si vous cherchez un outil facile pour calculer la hauteur dans n'importe quel triangle.

Dans cet article, nous nous pencherons sur les questions suivantes :

• Quelle est la définition de la hauteur d'un triangle ?
• Comment effectuer le calcul de la hauteur d'un triangle ?
• Comment calculer la hauteur d'un triangle équilatéral ?
• Comment calculer la hauteur d'un triangle isocèle ?
• Comment calculer la hauteur d'un triangle rectangle ?
• Comment utiliser ce calculateur de hauteur d'un triangle ?

Que vous recherchiez les formules de hauteur d'un triangle pour des triangles spéciaux tels que le triangle rectangle, équilatéral ou isocèle, ou pour un triangle scalène quelconque, ce calculateur est une valeur sûre. Il peut calculer les hauteurs de votre triangle, ainsi que ses côtés, ses angles, son périmètre et son aire. N'attendez plus, essayez-le !

Si vous vous demandez toujours quelle est la formule pour calculer la hauteur d'un triangle équilatéral ou comment trouver la hauteur sans connaître l'aire, continuez votre lecture et vous trouverez les réponses.

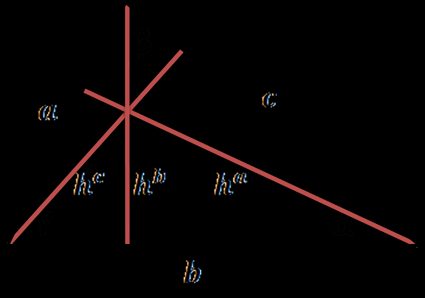
Chaque côté d'un triangle peut être une base, et à partir de chaque sommet, vous pouvez tracer une droite perpendiculaire à l'une des bases : le segment entre le sommet et la base est l'une des hauteurs du triangle en question. Chaque triangle a trois hauteurs. Pour en tracer une, il suffit de dessiner une ligne perpendiculaire à une base à partir du sommet opposé.

Il existe de nombreuses façons de trouver la hauteur d'un triangle. La plus répandue est celle qui utilise l'aire du triangle, mais il existe de nombreuses autres formules :

1. L'aire du triangle est donnée.

   L'équation bien connue de l'aire d'un triangle peut être transformée en une formule pour effectuer le calcul de la hauteur d'un triangle rectangle :

   $\mathrm{aire} = b \times h / 2$

   où :

   $b$ – la base
   $h$ – la hauteur

   Donc :

   $h = 2 \times \mathrm{aire} / b$

   Mais comment trouver la hauteur d'un triangle sans connaître l'aire ? Voici les formules les plus populaires :

2. Les côtés du triangle sont donnés.

   La formule de Héron vous permet de calculer l'aire à partir des côtés du triangle. Ensuite, comme vous connaissez l'aire, vous pouvez utiliser l'équation de base pour trouver la hauteur du triangle.

   Formule de Héron :

Par conséquent,

Consultez notre calculateur de formule de Héron 🇺🇸 pour en savoir plus sur cette équation.

3. Deux côtés et l'angle qui les sépare sont donnés.

   Utilisez la trigonométrie ou une autre formule pour calculer l'aire d'un triangle :

ou

$\mathrm{aire} = 0,\!5 \times a \times c \times \sin(\beta)$

ou

$\mathrm{aire} = 0,\!5 \times b \times c \times \sin(\alpha)$

si vous connaissez d'autres côtés.

Donc :

Si votre forme est un triangle spécial, poursuivez votre lecture pour trouver les formules de la hauteur d'un triangle. Dans le cas des triangles spéciaux, les formules sont simplifiées, et donc, plus faciles à retenir et à utiliser.

Vous pouvez également calculer la hauteur d'un triangle équilatéral avec notre calculateur de hauteur d'un triangle, mais voyons comment le faire à la main !

Un triangle équilatéral est un triangle dont les trois côtés sont égaux et dont les trois angles font $60\degree$. Les trois hauteurs ont la même longueur qui peut être calculée à l'aide de la formule suivante :

• $hΔ = a \times \sqrt{3} / 2$

  où : $a$ – un des côtés du triangle

Dans un triangle équilatéral, les hauteurs, les bissectrices des angles, les médiatrices et les médianes coïncident.

Si les formules de l'aire et du périmètre vous intéressent, consultez notre calculateur de triangle équilatéral.

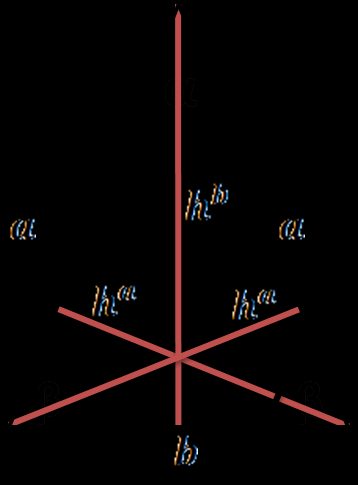
Un triangle isocèle est un triangle dont deux côtés sont de même longueur. Pour découvrir comment calculer la hauteur d'un triangle isocèle, vous devez d'abord savoir que ce type de triangle a deux hauteurs différentes.

• La hauteur qui part de l'apex est donnée par la formule suivante :

  $h_\mathrm{b} = \sqrt{a^2 - (0,\!5 \times b)^2}$

  où :

  $a$ – un des deux côtés égaux
  $b$ – la base

  Cette formule est dérivée du théorème de Pythagore.

• La hauteur qui part des sommets de la base peut être calculée de deux manières :

  Formule de l'aire :

Trigonométrie :

Pour obtenir les formules de l'aire et du périmètre de ce type de triangle, consultez notre calculateur de triangle isocèle.

Avant de commencer le calcul de la hauteur d'un triangle rectangle, sachiez que l des angles d'un triangle rectangle fait $90\degree$. Deux hauteurs sont faciles à trouver, car les côtés adjacents sont perpendiculaires : si le côté adjacent le plus court est une base, alors le côté adjacent le plus long est la hauteur, et vice versa. La troisième hauteur de ce triangle peut être calculée à partir de la formule suivante :

Et voilà ! Vous savez comment calculer la hauteur d'un triangle rectangle !

Si les formules de l'aire et du périmètre de ce triangle vous intéressent, consultez notre calculateur de triangle rectangle.

Après avoir lu notre explication, nous sommes presque sûrs que vous comprenez maintenant ce qu'est la hauteur d'un triangle et comment la trouver, même si l'aire n'est pas donnée. Mais examinons un exemple simple pour vous montrer la flexibilité de notre outil :

1. Choisissez le type de triangle. Supposons que nous voulions calculer les hauteurs d'un triangle scalène, nous ne changerons donc pas l'option par défaut.
2. Saisissez les valeurs données : soit trois côtés, soit deux côtés et un angle. Choisissons la première option : $a = 6\ \mathrm{cm}$, $b = 14\ \mathrm{cm}$, $c = 17\ \mathrm{cm}$.
3. Le calculateur de hauteur d'un triangle affichera les trois hauteurs : $13,\!17\ \mathrm{cm}$, $5,\!644\ \mathrm{cm}$, et $4,\!648\ \mathrm{cm}$. Le calculateur calculera également tous les angles, l'aire et le périmètre.

N'est-ce pas génial ?