Dernière mise à jour le: 07 Jul 2024

Calculateur de triangles rectangles particuliers

Q: Est-ce que 3, 4 et 5 forment un triplet pythagoricien ?

Oui . Les entiers a = 3 , b = 4 , et c = 5 forment un triplet pythagoricien puisque a² + b² = c² , et qu'un triangle dont les côtés sont abc est un triangle rectangle particulier.

Créé par Hanna Pamuła, Docteur·e

Revu par Bogna Szyk et Adena Benn

Adena Benn

LinkedInWebsite

Adena Benn is an Information Technology teacher with a degree in Computer Science. She has been teaching high schoolers since 1996 and loves everything computers. She loves problem-solving, so creating calculators to solve real-world problems is her idea of fun. She writes children's stories, is a seamstress, and is an avid reader. In her spare time, she travels and enjoys nature. See full profile

Check our editorial policy

Traduit par Claudia Herambourg

Claudia Herambourg

Claudia holds a bachelor’s degree in Literature and Mathematics from University College Cork, Ireland. Passionate by both words and numbers, she has never been able to pick a side. To nurture this quest to break the traditional disciplinary boundaries, Claudia obtained a certificate in data science. She believes in combining creative practice and data skills to comprehend and analyze existing stories and develop new narratives. After a long day, she either goes for a run or picks up her paintbrushes and canvas. See full profile

Check our editorial policy

et Clarissa Falempin

Nouveau

Sommaire

Demi-triangles équilatéraux : triangles 30-60-90 Triangles rectangles isocèles : triangles 45-45-90 Autres triangles rectangles particuliers Formules des triangles rectangles particuliers Caractéristiques des triangles rectangles particuliers Exemple : calculateur de triangles rectangles particuliers FAQ

Ce calculateur de triangles rectangles particuliers vous permettra de déterminer les mesures manquantes de votre triangle en un clin d'œil. Sélectionnez simplement le type de triangle souhaité et renseignez les valeurs connues. Les paramètres manquants seront automatiquement calculés.

Les triangles rectangles particuliers sont des triangles rectangles pour lesquels il existe des formules simples. Cela permet des calculs rapides, sans avoir recours au théorème de Pythagore ou à des méthodes plus complexes. Continuez à lire pour en savoir plus sur les formules et les caractéristiques des triangles rectangles spéciaux.

Demi-triangles équilatéraux : triangles 30-60-90

Le triangle rectangle $30\degree$ - $60\degree$ - $90\degree$ est l'un des triangles rectangles les plus connus. Ses propriétés sont uniques, car il s'agit de la moitié d'un triangle équilatéral, d'où son nom de demi-triangle équilatéral.

Si vous souhaitez en savoir plus sur cette forme particulière, consultez notre calculateur de demi-triangle équilatéral (30-60-90).

Triangles rectangles isocèles : triangles 45-45-90

Un autre triangle rectangle particulier courant est le triangle $45\degree$ - $45\degree$ - $90\degree$ . C'est le seul triangle rectangle possible qui soit aussi un triangle isocèle. C'est également la forme créée lorsque l'on coupe un carré le long de la diagonale :

Triangle rectangle isocèle : triangle 45-45-90 avec la longueur du côté adjacent indiquée.

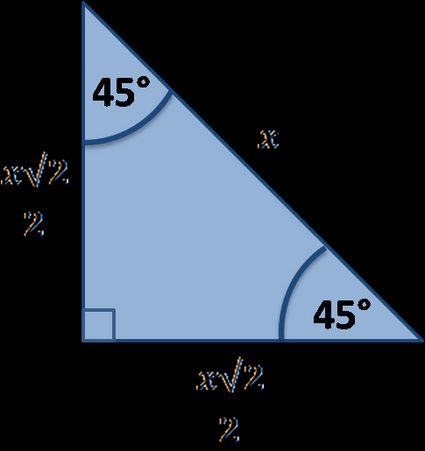
Triangle rectangle isocèle : triangle 45-45-90 avec la longueur de l'hypoténuse indiquée.

Vous êtes curieux ou curieuse de connaître les propriétés de ce triangle ? Consultez notre calculateur de triangle rectangle isocèle (45-90-90).

Autres triangles rectangles particuliers

Il existe de nombreux triangles rectangles particuliers, vous trouverez ci-dessous ceux qui sont traités par notre outil :

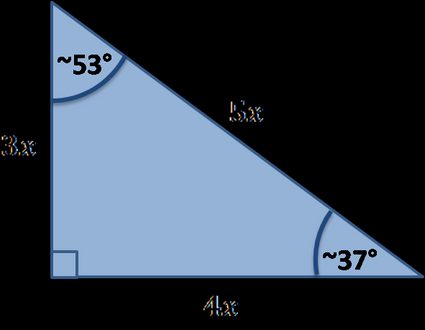
Triangle rectangle particulier : triangle 3x-4x-5x.

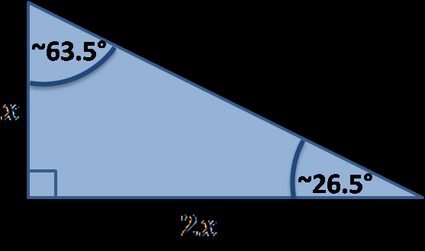
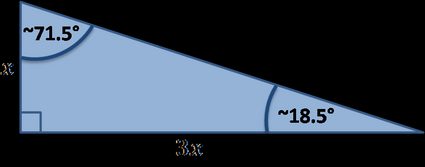
Formules des triangles rectangles particuliers

Triangle rectangle dont les côtés sont a, b, c et les angles α, β.

Si vous cherchez les formules des triangles rectangles particuliers, vous êtes au bon endroit. Jetez un coup d'œil au tableau ci-dessous, tout devrait devenir plus clair ! Dans ce tableau, vous trouverez les formules qui relient les angles des triangles rectangles particuliers, les côtés adjacents, l'hypoténuse, l'aire et le périmètre :

Triangle rectangle particulier	$a$ (Côté le plus court)	$b$ (Côté le plus long)	$c$ (Hypoténuse)	Aire	Périmètre	Angle $\alpha$	Angle $\beta$
$30\degree$ - $60\degree$ - $90\degree$	$x$	$x\sqrt 3$	$2x$	$x^2\sqrt{3}/2$	$x(3+\sqrt3)$	$30\degree$	$60\degree$
$45\degree$ - $45\degree$ - $90\degree$	$x$	$x$	$x\sqrt 2$	$x^2/2$	$x(2+\sqrt 2)$	$45\degree$	$45\degree$
$x$ - $2x$	$x$	$2x$	$x\sqrt5$	$x^2$	$x(3+\sqrt 5)$	$\sim26,\!5\degree$	$\sim63,\!5\degree$
$x$ - $3x$	$x$	$3x$	$x\sqrt {10}$	$3x^2/2$	$x(4+\sqrt{10})$	$\sim18,\!5\degree$	$\sim71,\!5\degree$
$3x$ - $4x$ - $5x$	$3x$	$4x$	$5x$	$6x^2$	$12x$	$\sim37\degree$	$\sim53\degree$

Caractéristiques des triangles rectangles particuliers

Les triangles rectangles particuliers sont des triangles rectangles qui présentent des caractéristiques spécifiques facilitant les calculs. La principale caractéristique d'un triangle rectangle particulier est bien sûr la présence d'un angle droit, associée à une propriété supplémentaire.

En général, on peut classer les triangles rectangles particuliers en deux groupes principaux.

Les triangles rectangles basés sur un angle, par exemple les triangles :
- $30\degree$ - $60\degree$ - $90\degree$
- $45\degree$ - $45\degree$ - $90\degree$
Les triangles rectangles basés sur les côtés. Ce sont des triangles dont les longueurs des côtés sont régies par une règle spécifique.
- Les triangles rectangles ayant des côtés avec des longueurs entières appelés triplets pythagoriciens, tels que :
  - $3:4:5$
  - $5:12:13$
  - $8:15:17$
  - $7:24:25$
  - $9:40:41$
- Les triangles rectangles ayant des côtés avec des longueurs entières, mais presque isocèles :
  - $20:21:29$
  - $119:120:169$
  - $696:697:985$
- Les triangles rectangles dont les côtés forment une suite géométrique (triangle de Kepler). Ils sont composés de trois côtés au carré. Leurs aires respectent une suite géométrique, selon le nombre d'or. Pour en savoir plus sur ce nombre particulier, consultez notre calculateur du nombre d'or.

Il existe de nombreuses règles et propriétés pour choisir un triangle et le qualifier de « particulier ». Dans notre calculateur de triangles rectangles particuliers, nous avons choisi cinq triangles : deux basés sur les angles et trois basés sur les côtés.

Exemple : calculateur de triangles rectangles particuliers

Prenons un exemple : nous voulons trouver la longueur de l'hypoténuse d'un triangle rectangle ayant un côté adjacent de $5\ \mathrm{cm}$ et un angle de $45\degree$ .

Choisissez le type de triangle rectangle particulier approprié. Dans notre cas, il s'agit du triangle $45\degree$ - $45\degree$ - $90\degree$ .
Entrez la valeur donnée. Nous savons que le côté est égal à $5$ , nous saisissons donc cette valeur dans le champ a ou b (ce dernier importe peu puisqu'il s'agit d'un triangle isocèle).
Ouah ! Le calculateur de triangles rectangles particuliers a trouvé les paramètres manquants de votre triangle ! Maintenant, nous savons que :
- le deuxième côté adjacent $b$ est égal à $5\ \mathrm{cm}$ ;
- l'hypoténuse $c$ est égale à $7,\!07\ \mathrm{cm}$ ;
- le périmètre est égal à $17,\!07\ \mathrm{cm}$ ; et
- l'aire de notre triangle particulier est de $12,\!5\ \mathrm{cm^2}$ .

N'attendez plus. Essayez-le vous-même !

FAQ

Quelles sont les formules pour un triangle rectangle isocèle 45-45-90 ?

Un triangle 45°-45°-90°, aussi dit triangle rectangle isocèle, a les propriétés suivantes, où x est la longueur d'un des côtés égaux :

hypoténuse = x√2
aire = x²/2
Périmètre = x(2+√2)

Comment résoudre un demi-triangle rectangle 30-60-90 ?

Pour résoudre un demi-triangle rectangle, ou simplement triangle 30°-60°-90°, procédez comme suit :

Trouvez la longueur du côté adjacent. Nous l'appellerons x.
Le côté adjacent sera égal à x√3.
Son hypoténuse sera égale à 2x.
L'aire est : A = x²√3/2.
Enfin, le périmètre est : P = x(3 + √3).

Quels sont les deux triangles particuliers en trigonométrie ?

Les triangles 30°-60°-90° (demi-triangle équilatéral) et 45°-45°-90° (triangle rectangle isocèle) sont les deux triangles particuliers en trigonométrie. Bien qu'il existe plus de deux triangles rectangles particuliers, ceux-ci sont les plus faciles à reconnaître et à résoudre. Un triangle rectangle dont les côtés forment un triplet pythagoricien est un exemple de triangle rectangle particulier non basé sur un angle.

Est-ce que 3, 4 et 5 forment un triplet pythagoricien ?

Oui. Les entiers a = 3, b = 4, et c = 5 forment un triplet pythagoricien puisque a² + b² = c², et qu'un triangle dont les côtés sont abc est un triangle rectangle particulier.