Calculateur de demi-triangle équilatéral (30-60-90)

Ce calculateur de demi-triangle équilatéral résout les mesures de ce triangle rectangle particulier. Que vous cherchiez les formules du demi-triangle équilatéral pour calculer l'hypoténuse, que vous vous interrogiez sur le rapport du demi-triangle équilatéral ou que vous vouliez simplement découvrir des informations sur ce triangle, vous êtes tombé.e sur le bon site. Continuez la lecture pour en savoir plus sur ce type de triangle rectangle, ou consultez l'outil dédié au jumeau de notre triangle – le calculateur de triangle isocèle.

Tout d'abord, expliquons ce que signifie « demi-triangle équilatéral ». C'est un triangle dont les angles sont égaux à 30°, 60° et 90°.

Supposons que le plus petit des côtés adjacents d'un demi-triangle équilatéral – son plus petit côté – est égal à a. Alors :

1. Le second côté adjacent est égal à a√3.
2. L'hypoténuse est égale à 2a.
3. L'aire est égale à a²√3/2.
4. Le périmètre est égal à a(3 + √3).

Les formules des demi-triangles équilatéraux sont assez faciles, mais quelles opérations mathématiques se cachent derrière ? Vérifions quelles méthodes utiliser pour prouver les formules :

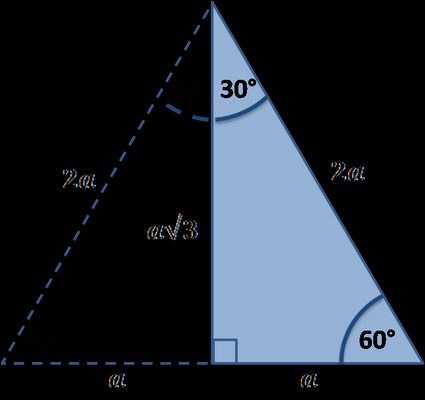
1. L'utilisation des propriétés du triangle équilatéral

Avez-vous remarqué que le triangle qui nous intéresse est simplement la moitié d'un triangle équilatéral ? Si vous vous souvenez de la formule de la hauteur d'un tel triangle régulier, alors vous connaissez la longueur du second côté adjacent – il est égal au côté du triangle équilatéral multiplié par la racine carrée de 3, le tout divisé par 2 :

h = c√3/2, h = b et c = 2a donc b = c√3/2 = a√3

2. L'utilisation de la trigonométrie

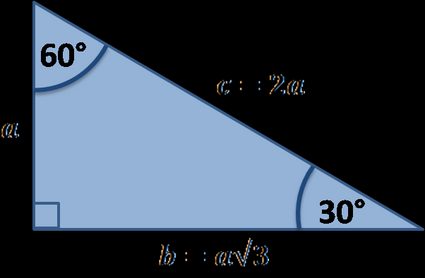
Si vous connaissez les bases de la trigonométrie, vous pouvez utiliser, par exemple, le sinus et le cosinus de 30° pour trouver les longueurs des autres côtés :

a/c = sin(30°) = 1/2 donc c = 2a

b/c = sin(60°) = √3/2 donc b = c√3/2 = a√3

De plus, si vous connaissez deux des côtés du triangle, vous pouvez trouver le troisième à partir du théorème de Pythagore. Cependant, les méthodes précédentes sont plus utiles, car elles peuvent être appliquées même si vous ne connaissez qu’un seul côté du demi-triangle équilatéral.

Si la longueur du plus court des côtés adjacents a est connue, il est possible de trouver :

• b = a√3

• c = 2a

Si on connait la valeur du côté adjacent plus long, b, alors :

• a = b√3/3

• c = 2b√3/3

Si l'hypoténuse c est la seule valeur connue, les formules des côtés adjacents sont les suivantes :

• a = c/2

• b = c√3/2

Vous pouvez également saisir les valeurs données, et le calculateur du demi-triangle équilatéral fera le reste !

La règle la plus importante à retenir est que ce triangle rectangle particulier a un angle droit et que ses côtés sont liés par un rapport constant – a : a√3 : 2a. Facile à retenir non ? De plus, la propriété inhabituelle de ce triangle 30 60 90 est qu'il s'agit du seul triangle rectangle dont les angles forment une progression arithmétique.

Qu'est-ce qu'une progression arithmétique ? Consulte notre calculateur de suites arithmétiques pour en savoir plus !

Dans un demi-triangle équilatéral, les rapports sont les suivants :

• 1 : 2 : 3 pour les angles (30° : 60° : 90°) ; et
• 1 : √3 : 2 pour les côtés (a : a√3 : 2a).

Après avoir vu toutes les règles et formules du demi-triangle équilatéral, il est arrivé le temps de mettre vos connaissances à l'épreuve !

1. Saisissez la valeur donnée. Prenons comme exemple notre équerre. Il s'agit d'un demi-triangle équilatéral, avec une règle graduée sur le côté adjacent le plus long. Celle-ci mesure 13 cm.
2. Les valeurs des autres côtés seront aussi bientôt visibles ! Grâce à ce calculateur de demi-triangle équilatéral, voici ce que l'on découvre.

• Le côté adjacent le plus court mesure 7,5 cm – car a = b√3/3 = 13 cm × √3/3 ≈ 7,5 cm.
• L'hypoténuse est égale à 12 cm – parce que c = 2b√3/3 = 2a ≈ 12 cm.
• L'aire est égale à 48,8 cm² – c'est le résultat de la multiplication de la longueur des côtés adjacents, divisé par 2 aire = (a²√3)/2 ≈ 48,8 cm².
• Le périmètre est égal à 35,5 cm – l'addition de tous les côtés donne ce résultat : périmètre = a + a√3 + 2a = a(3 + √3) ≈ 35,5 cm.