Calculateur de triangle rectangle isocèle (45-45-90)
Le calculateur de triangle rectangle isocèle est un outil dédié à la résolution de ce triangle rectangle particulier. Continuez la lecture pour découvrir les longueurs des côtés et de l'hypoténuse, ainsi que l'aire et le périmètre de votre triangle. Vous obtiendrez également des informations sur les formules, les rapports et les règles les plus susceptibles d'apparaitre dans vos exercices de mathématiques. Vous ne vous demanderez plus jamais comment faire pour résoudre un triangle rectangle isocèle !
Pour en savoir plus sur d'autres triangles rectangles connus, jetez un coup d'œil à ce calculateur de demi-triangle équilatéral et au calculateur de triangles rectangles spéciaux.
OK, ces formules de triangle rectangle isocèle semblent faciles, mais d'où viennent-elles ? Il existe plusieurs méthodes pour les prouver. Voici les plus connues :

-
Comme vous connaissez la longueur du côté adjacent a, vous connaissez aussi la longueur de l'autre, puisqu'ils sont égaux.
-
Trouvez l'hypoténuse à partir du théorème de Pythagore : on sait que
a² + b² = c²eta = b, donca² + a² = c²ce qui donne :
c = √(2a²) = a√2
- Les propriétés du carré
Avez-vous remarqué que le triangle rectangle isocèle est la moitié d'un carré coupé le long de sa diagonale ?
- Encore une fois, on sait que les deux côtés adjacents sont égaux à a.
- Vous vous souviendrez certainement que la diagonale du carré est égale à un côté multiplié par la racine carrée de 2, c'est-à-dire
a√2. Dans ce cas, cette diagonale est égale à l'hypoténuse du triangle. Trop facile !
- La trigonométrie
Si vous connaissez la trigonométrie, vous pourrez utiliser les propriétés du sinus et du cosinus. Pour cet angle spécial mesurant 45°, ils sont tous les deux égaux à √2/2. Ainsi,
a/c = √2/2, donc c = a√2.
Pour trouver l'aire de votre triangle, utilisez la formule de base pour calculer l'aire d'un triangle : aire = base × hauteur / 2. Dans ce cas, un côté adjacent est la base, et l'autre est la hauteur, puisqu'il y a un angle droit entre les deux. L'aire du triangle rectangle isocèle est donc la suivante :
aire = a² / 2
Pour calculer le périmètre, il suffit d'additionner tous les côtés du triangle rectangle isocèle :
périmètre = a + b + c = a + a + a√2 = a(2 + √2)
Les côtés du triangle rectangle isocèle
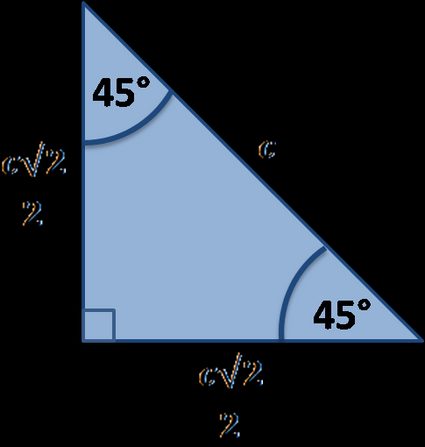

Quelles sont les règles du triangle rectangle isocèle ?
La règle la plus importante est que ce triangle a un angle droit, et que ses autres angles sont égaux à 45°. Cela signifie que deux de ces côtés – les côtés adjacents – sont égaux, le calcul de l'hypoténuse est alors facile. Les autres propriétés intéressantes du triangle rectangle isocèle sont les suivantes :
- C'est le seul triangle rectangle à être également un triangle isocèle.
- Son rapport entre l'hypoténuse et la somme des côtés adjacents est le plus petit de tous les triangles rectangles.
- Similairement, son rapport entre la hauteur issue de l'angle droit et la somme des longueurs des côtés adjacents est le plus grand de tous les triangles rectangles.
Les rapports des angles et des côtés dans un triangle rectangle isocèle
Dans un triangle rectangle isocèle, les rapports sont comme de suite :
- 1 : 1 : 2 pour les angles (45° : 45° : 90°) ; et
- 1 : 1 : √2 pour les côtés (a : a : a√2).
Un exemple de résolution d'un triangle rectangle isocèle
Jetez un coup d'œil à cet exemple pour découvrir les règles du triangle rectangle isocèle.
Supposons que vous vouliez résoudre le seul triangle isocèle d'un lot d'équerre :
- Saisissez la valeur donnée. L'un des côtés adjacents de l'équerre contient une règle ; la tactique la plus facile est donc de saisir cette longueur. D'habitude, elle mesure approximativement 23 cm. Saisissez cette valeur dans le champ a ou b.
- Le calculateur de triangle rectangle isocèle affichera les autres paramètres. Maintenant, on connait :
- la longueur de l'hypoténuse –
23 cm × √2 =32,5 cm ; - l'aire –
23 cm × 23 cm / 2 =264,5 cm² ; et - le périmètre –
23 cm + 23 cm + 23 cm × √2 =78,5 cm.
N'oubliez pas que les unités affichées peuvent être changées en cliquant simplement sur le nom de l'unité. De plus, souvenez-vous que notre calculateur de triangle rectangle isocèle est un outil flexible – si vous ne connaissez que la surface, l'hypoténuse ou même le périmètre, il peut également calculer les paramètres manquants. Génial !
Comment trouver l'aire d'un triangle rectangle isocèle dont le périmètre est donné ?
Si vous connaissez le périmètre d'un triangle rectangle isocèle, vous pouvez déterminer son aire de la manière suivante :
- Divisez le périmètre par
2 + √2, donc par environ3,41. - Le résultat de la première étape est le côté adjacent
ade votre triangle. - Élevez le côté adjacent au carré :
a². - Divisez le résultat par 2 :
a² / 2. - Voilà l'aire de votre triangle ! La formule complète est :
aire = [perimètre/(2 + √2)]² / 2.
Quelle est la mesure du côté adjacent d'un triangle rectangle isocèle dont le périmètre est égal à 10 ?
Approximativement 2,93. Pour arriver à ce résultat, on utilise la formule côté adjacent = périmètre/(2 + √2). Comme 2 + √2 est égal à environ 3,41, on obtient côté adjacent ≈ 10 / 3,41 ≈ 2,93. Si vous avez besoin d'un résultat plus précis, utilisez une approximation plus précise de √2.

Comment résoudre un triangle rectangle isocèle ?
Avez-vous besoin de formules pour résoudre un triangle rectangle isocèle ? Alors, vous êtes au bon endroit ! Si un côté adjacent du triangle est égal à a :