Calcolatore per Triangoli 30 60 90

Con questo calcolatore per triangoli 30 60 90 puoi risolvere le misure di questo speciale triangolo rettangolo. Se stai cercando le formule del triangolo 30 60 90 per l'ipotenusa, se ti stai chiedendo il rapporto tra i triangoli 30 60 90 o se vuoi semplicemente verificare l'aspetto di questo triangolo, hai trovato il sito giusto. Continua a scorrere per saperne di più su questo triangolo rettangolo specifico, oppure dai un'occhiata al nostro strumento per il gemello del nostro triangolo — calcolatore per triangoli 45 45 90.

Prima di tutto, spieghiamo cosa significa "30 60 90". Quando si parla di triangolo 30 60 90, si intendono gli angoli del triangolo, che sono uguali a 30°, 60° e 90°.

Supponiamo che il cateto più corto di un triangolo 30 60 90 sia uguale ad a. Allora:

• Il secondo cateto è uguale a a√3;
• L'ipotenusa è 2a;
• L'area è uguale a a²√3/2; e
• Il perimetro è uguale a a(3 + √3).

Le formule dei triangoli 30 60 90 sono piuttosto facili, ma qual è la matematica che le sottende? Verifichiamo quali metodi puoi utilizzare per dimostrarle:

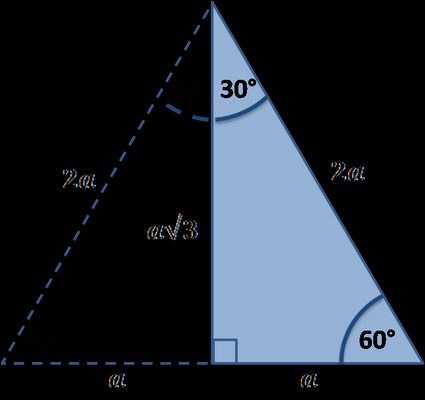
1. Utilizzando le proprietà del triangolo equilatero

Hai notato che il nostro triangolo di interesse è semplicemente la metà del triangolo equilatero? Se ricordi la formula per l'altezza di un triangolo regolare di questo tipo, hai la risposta per sapere qual è la lunghezza del secondo cateto. È uguale al lato moltiplicato per la radice quadrata di 3, diviso da 2:

h = c√3/2, h = b e c = 2a quindi b = c√3/2 = a√3

2. Utilizzando la trigonometria

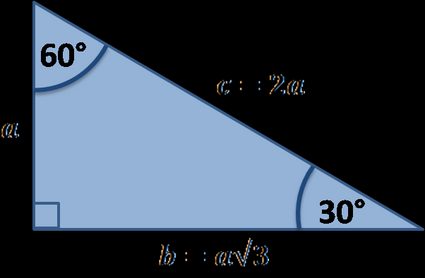
Se conosci le basi della trigonometria, puoi usare, ad esempio, il seno e il coseno di 30° per trovare la lunghezza degli altri lati:

a/c = sin(30°) = 1/2 quindi c = 2a

b/c = sin(60°) = √3/2 quindi b = c√3/2 = a√3

Inoltre, se conosci due lati del triangolo, puoi trovare il terzo dal teorema di Pitagora. Tuttavia, i metodi descritti in precedenza sono più utili in quanto è necessario conoscere solo un lato del triangolo 30 60 90.

Se conosciamo la lunghezza del cateto più corto a, possiamo scoprire che:

• b = a√3, e

• c = 2a.

Se la lunghezza del cateto più lungo b è l'unico dato che abbiamo a disposizione, allora:

• a = b√3/3, e

• c = 2b√3/3.

Per l'ipotenusa c nota, le formule dei cateti sono le seguenti:

• a = c/2, e

• b = c√3/2.

Oppure digita semplicemente i tuoi valori e il calcolatore per triangoli 30 60 90 farà il resto!

La regola più importante da ricordare è che questo speciale triangolo rettangolo ha un angolo retto e i suoi lati sono in un rapporto coerente tra loro facile da ricordare — il rapporto è a : a√3 : 2a. Inoltre, la proprietà insolita di questo triangolo 30 60 90 è che è l'unico triangolo rettangolo con angoli in sequenza aritmetica.

Cos'è una sequenza aritmetica? Consulta il nostro calcolatore per la progressione aritmetica per saperne di più!

I rapporti nel triangolo 30 60 90 sono:

• 1 : 2 : 3 per gli angoli (30° : 60° : 90°); e
• 1 : √3 : 2 per i lati (a : a√3 : 2a).

Hai letto le regole dei triangoli 30 60 90. Ora è arrivato il momento di fare pratica!

1. Inserisci il valore dato. Supponiamo di voler verificare come risolvere il triangolo 30 60 90 dal nostro insieme di triangoli. C'è una scala sul cateto più lungo. Supponiamo che la sua lunghezza sia di 30cm; e

2. Tutti gli altri valori sono apparsi! Grazie a questo calcolatore per triangoli 30 60 90, scoprirai che:

• Il cateto più corto è di 17,32 cm — perché a = b√3/3 = 30 cm × √3/3 ~ 17,32 cm,
• L'ipotenusa è uguale a 30,64 cm — perché c = 2b√3/3 = 2a ~ 30,64 cm,
• L'area è 260 cm² — è il risultato della moltiplicazione della lunghezza dei cateti e della divisione per 2 area = (a²√3)/2 ≈ 260 cm², e
• Il perimetro è pari a 82 cm — sommando tutti i lati si ottiene il risultato perimetro = a + a√3 + 2a = a(3 + √3) ≈ 82 cm.