Calcolatore per Triangoli 45 45 90

Il calcolatore per triangoli 45 45 90 è uno strumento dedicato alla risoluzione di questo speciale triangolo rettangolo. Scopri quali sono i lati, l'ipotenusa, l'area e il perimetro della tua forma e impara a conoscere le formule e i rapporti dei triangoli 45 45 90. Parleremo anche delle regole dei triangoli 45 45 90 che è più probabile che si presentino nei tuoi compiti a casa. Non dovrai mai più chiederti come risolvere un triangolo 45 45 90!

Se vuoi saperne di più su altri triangoli rettangoli popolari, dai un'occhiata a questo calcolatore per triangoli 30 60 90 e al calcolatore per triangoli rettangoli speciali.

Hai bisogno di formule per il triangolo 45 45 90? Sei nel posto giusto! Se il cateto del triangolo è uguale ad a, allora:

• Anche l'altro cateto sarà uguale a a;
• L'ipotenusa è a√2;
• L'area è uguale a a²/2; e
• Il perimetro è uguale a a(2 + √2).

Ok, queste formule dei triangoli 45 45 90 sembrano facili, ma da dove vengono? Esistono un paio di metodi per dimostrarle, i più popolari dei quali sono:

1. Usare il teorema di Pitagora

   • Poiché conosci la lunghezza di un cateto a, conosci anche la lunghezza dell'altro, poiché entrambi sono uguali.

   • Trova l'ipotenusa dal teorema di Pitagora:
     Abbiamo a² + b² = c² e a = b, quindi

     a² + a² = c²

     che dà

     c = √(2a²) = a√2

2. Utilizzando le proprietà del quadrato

   Hai notato che il triangolo 45 45 90 è la metà di un quadrato, tagliato lungo la diagonale del quadrato?

   • Anche in questo caso, sappiamo che entrambi i cateti sono uguali ad a.
   • Come probabilmente ricorderai, la diagonale del quadrato è uguale al lato moltiplicato per la radice quadrata di 2, ovvero a√2. Nel nostro caso, la diagonale è uguale all'ipotenusa. È stato veloce!

3. Usando la trigonometria

   Se conosci la trigonometria, puoi utilizzare le proprietà del seno e del coseno. Per questo angolo speciale di 45°, entrambi sono uguali a √2/2. Quindi:
   a/c = √2/2 quindi c = a√2

   Per trovare l'area del triangolo, usa la formula di base dell'area del triangolo, che è Area = base × altezza / 2. Nel nostro caso, un cateto è la base e l'altro è l'altezza, dato che tra loro c'è un angolo retto. Quindi l'area dei triangoli 45 45 90 è:

   Area = a² / 2

   Per calcolare il perimetro, è sufficiente sommare tutti i lati del triangolo 45 45 90:

   Perimetro = a + b + c = a + a + a√2 = a(2 + √2)

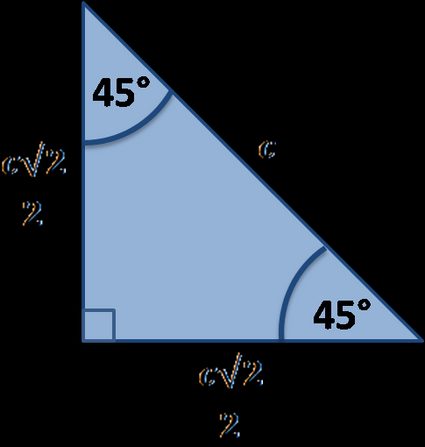
I cateti di questo triangolo sono uguali; l'ipotenusa si calcola immediatamente dall'equazione c = a√2. Se si possiede il valore dell'ipotenusa, la lunghezza del lato sarà uguale a a = c√2/2.

La regola più importante è che questo triangolo ha un solo angolo retto e gli altri due angoli sono uguali a 45°. Ciò implica che i due lati — i cateti — sono di lunghezza uguale e puoi calcolare facilmente l'ipotenusa. Le altre interessanti proprietà del triangolo 45 45 90 sono:

• È l'unico triangolo rettangolo possibile che è anche un triangolo isoscele;
• Di tutti i triangoli rettangoli, ha il rapporto più piccolo tra l'ipotenusa e la somma dei cateti; e
• Di tutti i triangoli rettangoli, ha il rapporto di altitudine maggiore tra l'ipotenusa e la somma dei cateti.

In un triangolo 45 45 90, i rapporti sono uguali a:

• 1 : 1 : 2 per gli angoli (45° : 45° : 90°); e
• 1 : 1 : √2 per i lati (a : a : a√2).

Dai un'occhiata a questo esempio reale per capire le regole del triangolo 45 45 90.

Supponiamo di voler risolvere il triangolo isoscele da un insieme di triangoli.

1. Digita il valore dato. Nel nostro caso, il modo più semplice è digitare la lunghezza della parte con la scala. La lunghezza tipica del cateto è di 23 cm, quindi digita questo valore nella casella a o b.
2. Il calcolatore per triangoli 45 45 90 mostra i parametri rimanenti. Ora sai che:

• Ipotenusa — 23 cm × √2 = 32,5 cm;
• Area — 23 cm × 23 cm / 2 = 264,5 cm²; e
• Perimetro — 23 cm + 23 cm + 23 cm × √2 = 78,5 cm.

Ricorda che puoi cambiare le unità di misura visualizzate semplicemente cliccando sul nome dell'unità. Inoltre, non dimenticare che il nostro calcolatore per triangoli 45 45 90 è uno strumento flessibile — se conosci solo l'area, l'ipotenusa o anche il perimetro, può calcolare anche i parametri rimanenti. Fantastico!