Ostatnia aktualizacja: Apr 30, 2024

Kalkulator szczególnych trójkątów prostokątnych

Q: Jakie są wzory na trójkąt 45 45 90?

Trójkąt 45° 45° 90° ma następujące wzory, gdzie x jest długością dowolnej z przyprostokątnych: Przeciwprostokątna = x√2 ; Pole = x²/2 ; oraz Obwód = x(2+√2) . Read more

Q: Czy 3, 4 i 5 to trójka pitagorejska?

Tak . Liczby całkowite a = 3 , b = 4 i c = 5 tworzą trójkąt pitagorejski, ponieważ a² + b² = c² , a trójkąt o powyższych bokach abc jest szczególnym trójkątem prostokątnym. Read more

Spis treści

Szczególne trójkąty prostokątne 30 60 90 Szczególny trójkąt prostokątny 45 45 90 Inne rodzaje szczególnych trójkatów prostokątnych Wzory szczególnych trójkątów prostokątnych Cechy szczególnych trójkątów prostokątnych Kalkulator szczególnych trójkątów prostokątnych — przykład FAQs

Nasz kalkulator szczególnych trójkątów prostokątnych pomoże ci obliczyć wymiary wybranego z listy trójkąta w mgnieniu oka. Wybierz trójkąt, który potrzebujesz i wpisz podane wartości — pozostałe parametry zostaną obliczone automatycznie.

Szczególne trójkąty prostokątne to trójkąty zawierające kąt prosty, dla których istnieją proste wzory. Pozwala to na szybkie obliczenia, więc nie musisz korzystać z twierdzenia Pitagorasa lub innych zaawansowanych metod. Przewiń w dół, aby przeczytać więcej o specjalnych wzorach i regułach w trójkątach prostokątnych.

Szczególne trójkąty prostokątne 30 60 90

Szczególny trójkąt prostokątny $30\degree$ $60\degree$ $90\degree$ jest jednym z najpopularniejszych trójkątów prostokątnych. Jego własności są wyjątkowe, ponieważ jest on połową trójkąta równobocznego.

Szczególny trójkąt prostokątny: 30-60-90.

Jeśli chcesz dowiedzieć się więcej o tym specjalnym kształcie, sprawdź nasz dedykowany kalkulator trójkąta 30° 60° 90°.

Szczególny trójkąt prostokątny 45 45 90

Innym znanym trójkątem prostokątnym jest trójkąt $45\degree$ $45\degree$ $90\degree$ . Jest to jedyny możliwy trójkąt prostokątny, który jest również trójkątem równoramiennym. Jest to również kształt powstały po przecięciu kwadratu wzdłuż przekątnej:

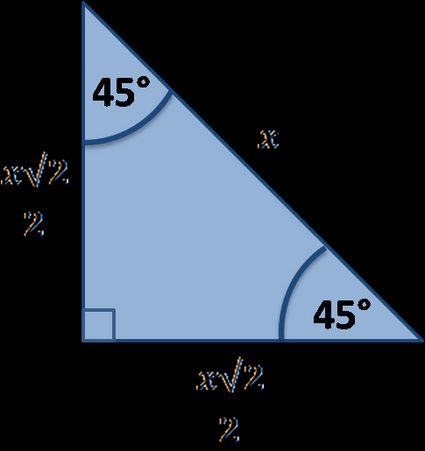
Szczególny trójkąt prostokątny 45 45 90 z podaną długością przeciwprostokątnej.

Interesują cię właściwości tego trójkąta? Sprawdź nasz kalkulator trójkątów 45° 45° 90°.

Inne rodzaje szczególnych trójkatów prostokątnych

Istnieje wiele specjalnych trójkątów prostokątnych, poniżej znajdziesz te zaimplementowane w naszym narzędziu:

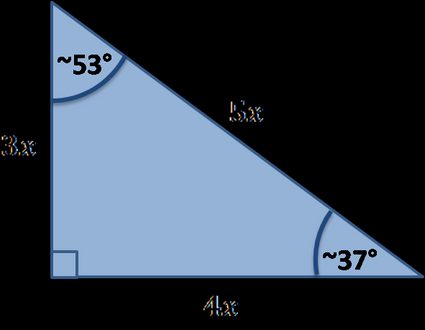
Szczególny trójkąt prostokątny: 3x-4x-5x.

Wzory szczególnych trójkątów prostokątnych

Trójkąt prostokątny o bokach a, b, c i kątach α, β.

Jeśli szukasz wzorów na szczególne trójkąty prostokątne, to jesteś we właściwym miejscu. Spójrz na poniższą tabelę; wszystko powinno być jasne! W tej tabeli znajdziesz wzory na związek między kątami trójkąta prostokątnego, bokami, przeciwprostokątną, polem i obwodem:

Szczególny trójkat prostokątny	$a$ (krótszy bok)	$b$ (dłuższy bok)	$c$ (przeciwprostokątna)	Pole	Obwód	Kąt $\alpha$	Kąt $\beta$
$30\degree$ - $60\degree$ - $90\degree$	$x$	$x\sqrt 3$	$2x$	$x^2\sqrt{3}/2$	$x(3+\sqrt3)$	$30\degree$	$60\degree$
$45\degree$ - $45\degree$ - $90\degree$	$x$	$x$	$x\sqrt 2$	$x^2/2$	$x(2+\sqrt 2)$	$45\degree$	$45\degree$
$x$ - $2x$	$x$	$2x$	$x\sqrt5$	$x^2$	$x(3+\sqrt 5)$	$\approx26,\!5\degree$	$\approx63,\!5\degree$
$x$ - $3x$	$x$	$3x$	$x\sqrt {10}$	$3x^2/2$	$x(4+\sqrt{10})$	$\approx18,\!5\degree$	$\approx71,\!5\degree$
$3x$ - $4x$ - $5x$	$3x$	$4x$	$5x$	$6x^2$	$12x$	$\approx37\degree$	$\approx53\degree$

Cechy szczególnych trójkątów prostokątnych

Szczególne trójkąty prostokątne to trójkąty, które mają pewne wyjątkowe cechy ułatwiające obliczenia. Oczywiście najważniejszą zasadą dotyczącą szczególnych trójkątów prostokątnych jest to, że muszą one mieć jeden kąt prosty oraz dodatkową charakterystyczną cechę. Ogólnie rzecz biorąc, specjalne trójkąty prostokątne można podzielić na dwie grupy:

Kątowe trójkąty prostokątne — na przykład trójkąty $30\degree$ - $60\degree$ - $90\degree$ i $45\degree$ - $45\degree$ - $90\degree$ .
Trójkąty prostokątne o konkretnych stosunkach długości boków — figury, których długości boków rządzą się określoną regułą, np:
- Boki o długościach określonych przez liczby naturalne nazywane trójkątami pitagorejskimi:
  
  $3:4:5$ , $5:12:13$ , $8:15:17$ , $7:24:25$ , $9:40:41$ …
- Boki o długościach całkowitych, ale trójkąty są niemal równoramienne:
  
  $20:21:29$ , $119:120:169$ , $696:697:985$ …
- Trójkąt prostokątny, którego boki są w ciągu geometrycznym (trójkąt Keplera). Tworzą go trzy boki kwadratu. Ich pola są w ciągu geometrycznym, zgodnie ze złotym podziałem. Aby dowiedzieć się więcej na temat tej szczególnej proporcji, odwiedź nasz kalkulator złotego podziału.

Istnieje wiele różnych zasad i opcji, dzięki którym możemy wybrać trójkąt i nazwać go szczególnym. W naszym kalkulatorze szczególnych trójkątów prostokątnych zaimplementowaliśmy pięć wybranych trójkątów: dwa kątowe i trzy o podanych stosunkach boków.

Kalkulator szczególnych trójkątów prostokątnych — przykład

Spójrzmy na przykład: chcemy znaleźć długość przeciwprostokątnej trójkąta, jeśli długość jednego boku wynosi $5$ cm, a jeden kąt ma $45\degree$ .

Wybierz odpowiedni typ szczególnego trójkąta prostokątnego. W naszym przypadku jest to trójkąt $45\degree$ - $45\degree$ - $90\degree$ .
Wpisz podaną wartość. Wiemy, że bok jest równy $5$ cm, więc wpisujemy tę wartość w polu a lub b — nie ma znaczenia gdzie, ponieważ jest to trójkąt równoramienny.
Wow! Kalkulator szczególnych trójkątów prostokątnych rozwiązał twoje zadanie! Teraz już wiemy, że:
- Drugi bok $b$ jest równy $5\ \mathrm{cm}$ ;
- Przeciwprostokątna $c$ jest równa $7,\!07\ \mathrm{cm}$ ;
- Obwód jest równy $17,\!07\ \mathrm{cm}$ ; oraz
- Pole naszego trójkąta wynosi $12,\!5\ \mathrm{cm^2}$ .

Nie ma na co czekać, wypróbuj nasze narzędzie, wprowadzając własne wartości!

FAQs

Jakie są wzory na trójkąt 45 45 90?

Trójkąt 45° 45° 90° ma następujące wzory, gdzie x jest długością dowolnej z przyprostokątnych:

Przeciwprostokątna = x√2;
Pole = x²/2; oraz
Obwód = x(2+√2).

Jak rozwiązać trójkąt prostokątny 30 60 90?

Aby rozwiązać specjalny trójkąt prostokątny 30° 60° 90°, wykonaj następujące kroki:

Znajdź długość krótszego boku. Nazwiemy go a.
Dłuższy bok będzie równy a√3.
Przeciwprostokątna będzie równa 2a.
Pole wynosi A = a²√3/2.
Obwód wynosi P = a(3 + √3).

Jakie są dwa szczególne trójkąty w trygonometrii?

Trójkąty 30° 60° 90° i 45° 45° 90° (lub trójkąt równoramienny prosty) to dwa szczególne typy trójkątów. Chociaż istnieje ich więcej, te są najszybsze do rozpoznania i najłatwiejsze do obliczenia. Przykładem specjalnego trójkąta prostokątnego nieopartego na kątach jest trójkąt prostokątny, którego boki tworzą trójki pitagorejskie.

Czy 3, 4 i 5 to trójka pitagorejska?

Tak. Liczby całkowite a = 3, b = 4 i c = 5 tworzą trójkąt pitagorejski, ponieważ a² + b² = c², a trójkąt o powyższych bokach abc jest szczególnym trójkątem prostokątnym.

Szczególny trójkąt

a

b

c

Obwód

Pole

Check out 19 similar triangle calculators 🔺

30 60 90 triangle45 45 90 triangleArea of a right triangle...16 more