Kalkulator trójkąta 30 60 90

Z naszym Omni kalkulatorem trójkąta 30 60 90 możesz rozwiązać zadania związane z tym szczególnym trójkątem prostokątnym. Niezależnie od tego, czy szukasz wzorów na trójkąt 30 60 90 i jego przeciwprostokątną, zastanawiasz się nad proporcjami trójkąta 30 60 90, czy po prostu chcesz sprawdzić, jak wygląda ten trójkąt — zapewniamy, że jesteś we właściwym miejscu. Czytaj dalej, aby dowiedzieć się więcej o tym szczególnym trójkącie prostokątnym, lub sprawdź nasze bliźniacze narzędzie dla innego trójkąta — trójkąta 45 45 90.

Zacznijmy od wyjaśnienia, co oznaczają liczby „30 60 90”. Jeśli mówimy o trójkącie 30 60 90, mamy na myśli kąty trójkąta, które są równe 30°, 60° i 90°.

Przyjmijmy, że krótsza przyprostokątna trójkąta 30 60 90 jest równa a. Wtedy:

• Dłuższa przyprostokątna jest równa a√3.
• Przeciwprostokątna jest równa 2a.
• Pole jest równe a²√3/2.
• Obwód jest równy a(3 + √3).

Jak widzisz, wzory związane z trójkątem 30 60 90 są dość proste. Ale skąd się wzięły? Sprawdźmy, jakich metod można użyć do ich udowodnienia:

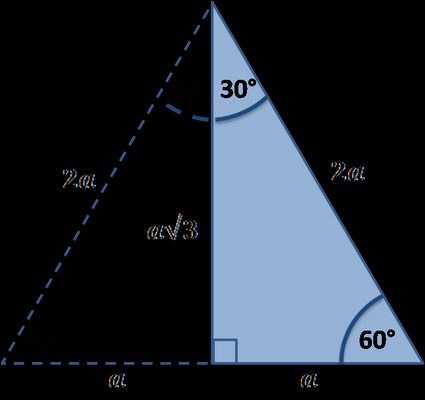
1. Zastosuj własności trójkąta równobocznego.

Czy zauważyłeś, że ten trójkąt to po prostu połowa trójkąta równobocznego? Jeśli pamiętasz wzór na wysokość trójkąta równobocznego, to masz odpowiedź na to, jaka jest długość dłuższej przyprostokątnej. Jest ona równa bokowi trójkąta pomnożonemu przez pierwiastek kwadratowy z 3, podzielony przez 2:

h = c√3/2, h = b oraz c = 2a, więc
b = c√3/2 = a√3.

2. Wykorzystaj trygonometrię.

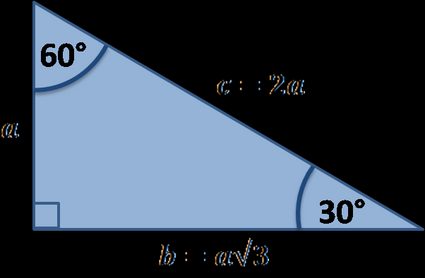
Jeśli znasz już podstawy trygonometrii, to możesz wykorzystać np. sinus i cosinus kąta 30°, aby znaleźć długości pozostałych boków:

a/c = sin(30°) = 1/2 więc c = 2a.

b/c = sin(60°) = √3/2 więc b = c√3/2 = a√3.

Ponadto, jeśli znasz dwa boki trójkąta, to trzeci możesz znaleźć z twierdzenia Pitagorasa. Jednakże opisane powyżej metody są o wiele bardziej przydatne, gdyż wymagają podania tylko jednego boku trójkąta 30 60 90.

Jeśli znamy długość krótszego boku a, to możemy stwierdzić, że:

• b = a√3

• c = 2a

Jeśli dłuższa przyprostokątna b jest naszą daną, to:

• a = b√3/3

• c = 2b√3/3

Dla znanej długości przyprostokątnej c, wzory na pozostałe boki wyglądają następująco:

• a = c/2

• b = c√3/2

Możesz też po prostu wpisać którykolwiek bok w nasze narzędzie, a kalkulator trójkąta 30 60 90 zrobi resztę!

Najważniejszą zasadą, którą warto zapamiętać, jest informacja, że ten szczególny trójkąt ma jeden kąt prosty, a stosunek długości jego boków jest łatwy do zapamiętania — stosunek ten wynosi a : a√3 : 2a. Ponadto niezwykłą własnością trójkąta 30 60 90 jest to, że jest to jedyny trójkąt prostokątny z wartościami kątów będących ciągiem arytmetycznym.

Co to jest ciąg arytmetyczny? Sprawdź nasz kalkulator ciągu arytmetycznego aby dowiedzieć się więcej!

W trójkącie 30 60 90 stosunki wynoszą:

• 1 : 2 : 3 dla kątów (30° : 60° : 90°), oraz
• 1 : √3 : 2 dla boków (a : a√3 : 2a).

Z naszego artykułu powinniście znać już zasady rozwiązywania trójkątów 30 60 90. Teraz najwyższy czas, abyście zastosowali zdobytą wiedzę!

1. Wprowadź daną wartość. Powiedzmy, że chcemy sprawdzić, jak wyznaczyć długości boków i kątów dla trójkąta 30 60 90 z naszego zestawu ekierek. Na dłuższym boku (dłuższej przyprostokątnej) znajduje się skala. Przyjmijmy, że ta długość wynosi 15 cm. Wpisz więc 15 w pole kalkulatora oznaczone literką b.
2. Tylko spójrz! Wszystkie pozostałe wartości się pojawiły w kalkulatorze! Dzięki kalkulatorowi trójkąta 30 60 90 dowiadujemy się, że:

• Krótsza przyprostokątna ma długość 8,66 cm — bo a = b√3/3 = 15 cm ∙ √3/3 ≈ 8,66 cm.
• Przeciwprostokątna jest równa 17,32 cm — bo c = 2b√3/3 = 2a ≈ 17,32 cm.
• Pole powierzchni wynosi 65 cm² — to wynik wymnożenia długości przyprostokątnych i podzielenia przez 2: pole = a²√3/2 ≈ 65 cm².
• Obwód jest równy 41 cm — dodając wszystkie boki otrzymujemy taki właśnie wynik: obwód = a + a√3 + 2a = a(3 + √3) ≈ 41 cm.