Kalkulator trójkąta 45 45 90

Kalkulator trójkąta 45 45 90 to dedykowane narzędzie do rozwiązywania tego szczególnego trójkąta prostokątnego. Tutaj dowiesz się, jakiej długości są wszystkie trzy boki — dwie przyprostokątne i przeciwprostokątna — jakie jest pole i obwód twojego trójkąta oraz poznasz wzory i proporcje charakteryzujące trójkąt 45 45 90. Omówimy również własności dotyczące trójkąta 45 45 90, które najprawdopodobniej pojawią się w twoich zadaniach domowych. Już nigdy więcej nie będziesz się zastanawiać, jak rozwiązać zadanie z trójkątem 45 45 90!

Jeśli chcesz dowiedzieć się więcej o innych popularnych trójkątach prostokątnych, sprawdź nasz kalkulator trójkąta 30 60 90 oraz kalkulator szczególnych trójkątów prostokątnych.

Na początku, należy się słowo wyjaśnienia — co tak właściwie oznaczają liczby „45 45 90”? Jeśli mowa jest o trójkącie 45 45 90, mamy na myśli kąty trójkąta, które są równe 45°, 45° i 90°.

Potrzebujesz wzorów opisujących trójkąt 45 45 90? Jesteś we właściwym miejscu! Jeśli jedna przyprostokątna trójkąta jest równa a, to:

• Druga przyprostokątna jest również równa a.
• Przeciwprostokątna jest równa a√2.
• Pole jest równe a²/2.
• Obwód jest równy a(2 + √2).

OK, te wzory na trójkąt 45 45 90 wyglądają łatwo, prawda? Ale... skąd się właściwie wzięły? Jest kilka metod na ich wyprowadzenie , a najpopularniejsze z nich to:

1. Wykorzystanie twierdzenia Pitagorasa.

• Skoro znasz długość jednej przyprostokątnej a, to znasz też długość drugiej, bo są sobie równe.

• Znajdź przeciwprostokątną z twierdzenia pitagorejskiego. Skoro a² + b² = c² i a = b, tak więc otrzymujemy:

  a² + a² = c²

  co daje ostatecznie:

  c = √(2a²) = a√2

2. Skorzystanie z własności kwadratu.

Czy zauważyłeś, że trójkąt 45 45 90 jest połową kwadratu, przeciętą wzdłuż jego przekątnej?

• Analogicznie, wiemy, że obie przyprostokątne są równe a.
• Jak zapewne pamiętasz, przekątna kwadratu jest równa bokowi razy pierwiastek kwadratowy z 2, czyli a√2. W naszym przypadku ta przekątna jest równa przeciwprostokątnej.

Tym razem poszło naprawdę błyskawicznie!

3. Zastosowanie trygonometrii.

Jeśli znasz trygonometrię, możesz wykorzystać własności sinusa i cosinusa. Dla naszego specjalnego kąta 45°, zarówno sinus jak i cosinus są równe √2/2, zatem:
a/c = √2/2, więc c = a√2

Aby znaleźć pole trójkąta 45 45 90, należy skorzystać z podstawowego wzoru na tę wielkość, czyli:

pole = podstawa ∙ wysokość / 2

W naszym przypadku jedna przyprostokątna jest podstawą, a druga wysokością, gdyż między nimi jest kąt prosty. Pole powierzchni trójkąta 45 45 90 wynosi więc:

pole = a² / 2

Aby obliczyć obwód, wystarczy dodać wszystkie boki:

obwód = a + b + c = a + a + a√2 = a(2 + √2)

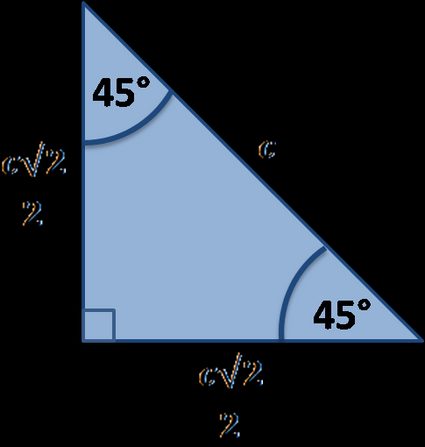
Jak już wiemy, przyprostokątne takiego trójkąta są równe; zaś przeciwprostokątną obliczamy bezpośrednio z równania c = a√2. Jeśli znamy wartość przeciwprostokątnej, to długość boku będzie równa a = c√2/2.

Najważniejsza zasada mówi, że ten trójkąt ma jeden kąt prosty, a dwa pozostałe kąty są równe 45°. Wynika z tego, że dwa boki — przyprostokątne — są równej długości i dzięki temu łatwo można obliczyć przeciwprostokątną. Inne ciekawe własności trójkąta 45 45 90 to:

• Jest to jedyny rodzaj trójkąta prostokątnego, który jest jednocześnie trójkątem równoramiennym.
• Ma on najmniejszy stosunek długości przeciwprostokątnej do sumy przyprostokątnych.
• Ma największy stosunek wysokości opuszczonej z wierzchołka kąta prostego do sumy przyprostokątnych.

W trójkącie 45 45 90 stosunki są równe:

• 1 : 1 : 2 dla kątów (45° : 45° : 90°), oraz
• 1 : 1 : √2 dla boków (a : a : a√2).

Przeanalizujmy teraz jeden przykład, aby lepiej zrozumieć zasady rozwiązywania zadań z trójkątami 45 45 90.

Załóżmy, że chcemy rozwiązać trójkąt równoramienny — ten z naszego zestawu ekierek.

1. Podajemy daną. W naszym przypadku najprościej będzie wpisać długość boku z podziałką. Załóżmy, że długość przyprostokątnej wynosi 9 cm. Wpisz tę wartość w polu a lub b.
2. Kalkulator trójkąta 45 45 90 pokazuje wszystkie pozostałe parametry. Teraz już wiesz, że:

• długość przeciwprostokątnej — 9 cm ∙ √2 ≈ 12,73 cm;
• pole powierzchni — 9 cm ∙ 9 cm / 2 = 40,5 cm²; oraz
• obwód — 9 cm + 9 cm ∙ √2 ≈ 30,7 cm.

Pamiętaj, że możesz zmienić wyświetlane jednostki, klikając na nazwę jednostki. Nie zapominaj również, że nasz kalkulator trójkątów 45 45 90 jest narzędziem bardzo elastycznym i wykonującym obliczenia w różnych kierunkach — jeśli znasz tylko i wyłącznie pole, samą przeciwprostokątną lub nawet dany jest tylko obwód, narzędzie to może szybko pomóc ci obliczyć pozostałe parametry. Ekstra! 😎