Kalkulator redukcji kąta

Nasz kalkulator redukcji kąta to poręczne narzędzie do przeliczania kątów na ich wersje z pierwszej ćwiartki. Wystarczy, że wpiszesz w pole dowolny kąt, a kalkulator znajdzie kąt odniesienia, zwany też kątem referencyjnym.

Poniższy artykuł wyjaśnia definicję kąta odniesienia. Znajdziesz w nim również instrukcję krok po kroku jak dokonywać redukcji kąta (danego w radianach lub w stopniach) oraz kilka przykładów. Przewiń nieco niżej — zaczynamy od wykresu ćwiartek.

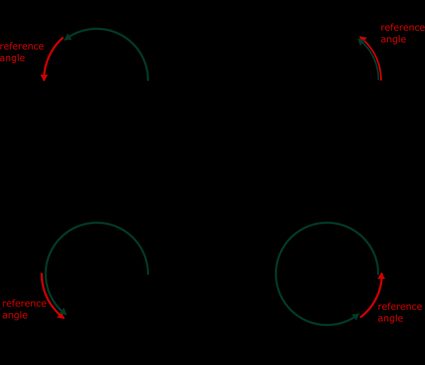
Spójrz na powyższy rysunek. Każdy kąt jest mierzony od dodatniej części osi x (poziomej) do półprostej, która wyznacza drugie ramię kąta. Poruszamy się przy tym w kierunku przeciwnym do ruchu wskazówek zegara. Jeśli chcesz znaleźć kąt odniesienia, musisz zredukować swój kąt do pierwszej ćwiartki, tzn. wyznaczyć najmniejszy możliwy kąt utworzony przez oś x (również jej ujemną część!) i drugie ramię, poruszając się zgodnie lub przeciwnie do ruchu wskazówek zegara.

Redukcja kąta jest niezwykle przydatna w trygonometrii. Jeśli chcesz znaleźć sinus lub cosinus dowolnego kąta, musisz najpierw poszukać jego kąta odniesienia w pierwszej ćwiartce. Następnie znajdujesz funkcję trygonometryczną zredukowanego kąta, dobierasz odpowiedni znak i gotowe.

Najczęściej spotykane kąty i ich funkcje trygonometryczne można znaleźć w poniższej tabeli:

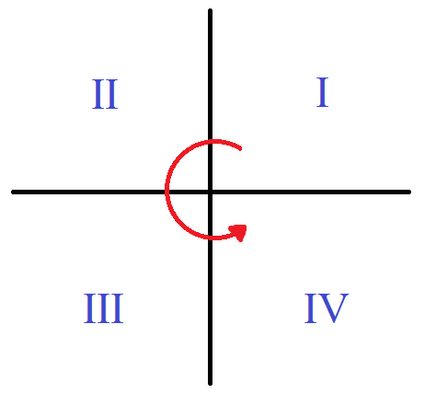
Dwie osie układu współrzędnych kartezjańskich dzielą płaszczyznę na cztery nieskończone obszary zwane ćwiartkami. Numeracja zaczyna się od prawej górnej ćwiartki, gdzie obie współrzędne są dodatnie. Następnie posuwamy się w kierunku przeciwnym do ruchu wskazówek zegara, jak na rysunku.

Funkcje trygonometryczne (sinus, cosinus, tangens, cotangens) przyjmują niemal tę samą wartość zarówno dla kąta, jak i jego kąta odniesienia. Niemal, ponieważ może zmieniać się znak — funkcje te są dodatnie bądź ujemne w różnych ćwiartkach, zgodnie ze słynnym wierszykiem:

W pierwszej wszystkie są dodatnie,
w drugiej tylko sinus,
w trzeciej tangens i cotangens,
a w czwartej cosinus.

(Alternatywna wersja rozpoczyna się słowami w pierwszej ćwiartce same plusy itd.)

Możesz spotkać się też z wersją angielską, która brzmi dość tajemniczo: All Students Take Calculus. Klucz do zagadki tkwi w pierwszych literach (ASTC), które tłumaczymy następująco:

A jak all, czyli wszystkie: w pierwszej ćwiartce wszystkie funkcje trygonometryczne mają wartości dodatnie.

• S jak sinus: w drugiej ćwiartce tylko funkcja sinus ma wartości dodatnie.
• T jak tangens: w trzeciej ćwiartce tangens i cotangens mają wartości dodatnie.
• C jak cosinus: w czwartej ćwiartce tylko funkcja cosinus ma wartości dodatnie.

Ponieważ clou tkwi w pierwszych literach, wyobraźnia ma tu duże pole do popisu! Oto kilka propozycji anglojęzycznych:

• All Stations To Central 🚆
• Add Sugar To Coffee ☕
• All Science Teachers (are) Crazy 👩‍🏫

Możesz spróbować wymyślić swoją wersję, czy to po polsku, czy po angielsku — najważniejsze to ją zapamiętać! Potem odwiedź nasz kalkulator twierdzenia sinusów oraz kalkulator twierdzenia cosinusów 🇺🇸, aby nauczyć się jeszcze więcej o trygonometrii!

Wystarczy, że wykonasz poniższe kroki:

1. Wybierz kąt początkowy — na przykład 610°.

2. Jeśli twój kąt jest większy niż 360° (kąt pełny), odejmij 360°. Jeśli trzeba, zrób to kilka razy, aż uzyskasz kąt mniejszy od kąta pełnego. Innymi słowy, wyznacz wartość kąta modulo 360°. W naszym przykładzie, po odjęciu 360° od 610° otrzymujemy 250°.

3. Określ, w której ćwiartce leży twój kąt:

   • 0° do 90° — pierwsza ćwiartka,
   • 90° do 180° — druga ćwiartka,
   • 180° do 270° — trzecia ćwiartka,
   • 270° do 360° — czwarta ćwiartka.

   W naszym przypadku 250° leży w trzeciej ćwiartce.

4. Wybierz właściwy wzór redukcyjny na obliczenie kąta referencyjnego:

   • 0° do 90°: kąt odniesienia = kąt początkowy,
   • 90° do 180°: kąt odniesienia = 180° - kąt początkowy,
   • 180° do 270°: kąt odniesienia = kąt początkowy - 180°,
   • 270° do 360°: kąt odniesienia = 360° - kąt początkowy.

   W naszym przykładzie musimy zastosować wzór kąt odniesienia = kąt początkowy - 180°.

5. Podstaw swój kąt do wzoru redukcyjnego:

   kąt odniesienia = 250° - 180° = 70°.

Jeśli potrzebujesz narzędzia do konwersji pomiędzy różnymi jednostkami miary kąta, wypróbuj nasz przelicznik kątów 🇺🇸.

To łatwiejsze niż się wydaje!

1. Dla kątów większych niż 2π odejmuj wielokrotności 2π, aż zostanie ci wartość mniejsza niż kąt pełny.
2. Wybierz właściwy wzór w zależności od ćwiartki:

• 0 do π/2 — pierwsza ćwiartka, zatem kąt odniesienia = kąt początkowy;
• π/2 do π — druga ćwiartka, zatem kąt odniesienia = π - kąt początkowy;
• π do 3π/2 — trzecia ćwiartka, zatem kąt odniesienia = kąt początkowy- π; oraz
• 3π/2 do 2π — czwarta ćwiartka, zatem kąt odniesienia = 2π - kąt początkowy.

Jak widzisz, procedura ta jest podobna do tej dla stopni. Jako przykład rozważmy kąt o mierze 28π/9 radianów.

1. Po odjęciu wielokrotności 2π, pozostaje nam 10π/9.
2. 10π/9 jest nieco większy od π, więc leży w trzeciej ćwiartce. Wzór na redukcję kąta to:

kąt odniesienia = kąt początkowy - π = π/9

To bardzo proste:

1. Wpisz kąt w pole kalkulatora. Może to być dowolny kąt dodatni; powiedzmy, że chcemy znaleźć kąt odniesienia dla 210°. Jeśli chcesz, możesz też zmienić jednostki, np. na radiany.
2. Kalkulator redukcji kąta znajduje kąt odniesienia jak również ćwiartkę, w której leży twój kąt początkowy. W naszym przypadku jest to 30°, a kąt początkowy leży w trzeciej ćwiartce. Super!

Jeśli chcesz szybkiej odpowiedzi, spójrz na poniższą tabelę:

Pierwsza ćwiartka:

Druga ćwiartka

Trzecia ćwiartka

Czwarta ćwiartka