Calculadora de Ângulos de um Triângulo

A calculadora de ângulos de triângulos da Omni é uma aposta segura se você quiser saber como encontrar o ângulo de um triângulo. Quer você tenha três lados de um triângulo, dois lados e um ângulo ou apenas dois ângulos, essa ferramenta é a solução para seus problemas de geometria. Abaixo, você também encontrará a explicação das leis fundamentais relativas aos ângulos dos triângulos: teorema da soma dos ângulos do triângulo, teorema do ângulo externo do triângulo e teorema da bissetriz do ângulo. Continue lendo para entender como a calculadora funciona e experimente. Encontrar ângulos ausentes em triângulos nunca foi tão fácil!

Há várias maneiras de encontrar os ângulos em um triângulo, dependendo do que é dado:

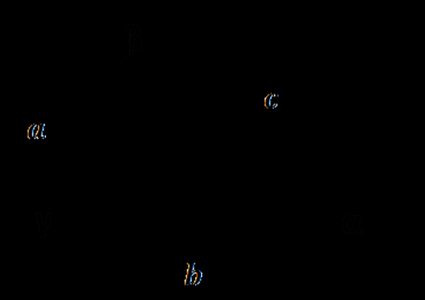
1. Dados três lados do triângulo

Use as fórmulas transformadas a partir da lei dos cossenos:

Então:

Para o segundo ângulo, temos:

Então:

E, por fim, para o terceiro ângulo:

Então:

2. Dados dois lados do triângulo e um ângulo

Se o ângulo estiver entre os lados dados, você pode usar diretamente a lei dos cossenos para encontrar o terceiro lado desconhecido e, em seguida, usar as fórmulas acima para encontrar os ângulos que faltam, por exemplo, dados a,b,γ:

• calcule $c = \sqrt{a^2 + b^2 - 2ab \times \cos(\gamma)}$;
• substitua $c$ por $\alpha = \mathrm{arccos}\left((b^2 + c^2- a^2)/(2bc)\right)$;
• em seguida, encontre $\beta$ com base no teorema da soma dos ângulos do triângulo: $\beta = 180\degree- \alpha - \gamma$

Se o ângulo não estiver entre os lados fornecidos, você pode usar a lei dos senos. Por exemplo, suponha que você conheça $a$, $b$ e $\alpha$:

Então:

• Como você sabe, a soma dos ângulos em um triângulo é igual a $180\degree$. A partir desse teorema, podemos encontrar o ângulo que falta: $\gamma = 180\degree- \alpha - \beta$.

3. Dados dois ângulos

Essa é a opção mais fácil. Basta você usar o teorema da soma dos ângulos do triângulo para encontrar o ângulo que falta:

• $\alpha = 180\degree- \beta - \gamma$;
• $\beta= 180\degree- \alpha - \gamma$; e
• $\gamma = 180\degree- \alpha- \beta$

Em todos os três casos, você pode usar nossa calculadora de ângulos triangulares da Omni. Você não irá se desapontar!

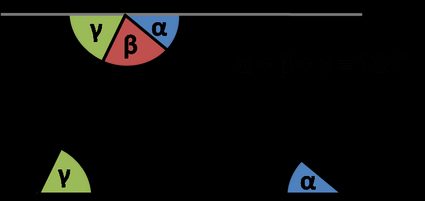
O teorema afirma que a soma dos ângulos internos de um triângulo é igual a $180\degree$:

Como sabemos disso? Observe a figura: os ângulos indicados com as mesmas letras gregas são congruentes porque são ângulos internos alternados. A soma dos três ângulos $\alpha$ , $\beta$ , $\gamma$ é igual a $180\degree$, pois eles formam uma linha reta. Mas esses são três ângulos internos em um triângulo! É por isso que $\alpha + \beta+ \gamma = 180\degree$.

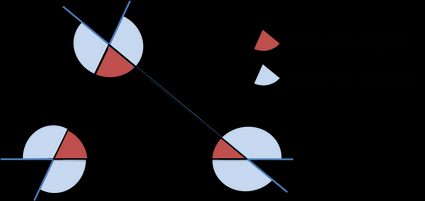
Um ângulo externo de um triângulo é igual à soma dos ângulos internos opostos.

• Todo triângulo tem seis ângulos externos (dois em cada vértice têm a mesma medida).
• Os ângulos externos, tomados um em cada vértice, sempre somam $360\degree$.
• Um ângulo externo é suplementar ao ângulo interno de seu triângulo adjacente.

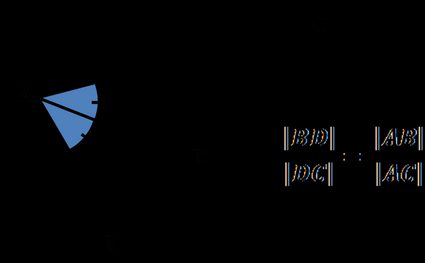
O teorema da bissetriz do ângulo afirma que:

A bissetriz de um ângulo de um triângulo divide o lado oposto em dois segmentos que são proporcionais aos outros dois lados do triângulo

Ou, em outras palavras:

A razão entre o comprimento de $\overline{BD}$ e o comprimento de $\overline{DC}$ é igual à razão entre o comprimento do lado $\overline{AB}$ e o comprimento do lado $\overline{AC}$:

Agora vamos praticar o que acabamos de ler. Suponhamos que você queira encontrar os ângulos que faltam em nosso triângulo. Como fazer isso?

1. Descubra quais fórmulas você precisa usar. Em nosso exemplo, temos dois lados e um ângulo. Escolha a opção ângulo e 2 lados.
2. Digite os valores fornecidos. Por exemplo, sabemos que $a = 9\ \mathrm{cm}$, $b = 14\ \mathrm{cm}$, e $\alpha = 30\degree$. Se você quiser calcular manualmente, use a lei dos senos:

Então:

• Com base no teorema sobre a soma dos ângulos em um triângulo, calculamos que $\gamma = 180\degree- \alpha - \beta = 180\degree- 30\degree - 51,\!06\degree= 98,\!94\degree$.

3. A nossa calculadora de ângulos de triângulos encontra os ângulos que faltam no triângulo. Eles são iguais aos que calculamos manualmente:$\beta = 51,\!06\degree$, $\gamma = 98,\!94\degree$. Além disso, a ferramenta determinou o comprimento do último lado: $c = 17,\!78\ \mathrm{cm}$.

Um raciocínio semelhante ao que aplicamos nessa calculadora aparece em outros cálculos envolvendo triângulos, por exemplo, os que usamos na calculadora de triângulos ALA 🇺🇸 e na calculadora de triângulos LLA 🇺🇸, ambas da Omni!