Calculadora de Área da Superfície de Prisma Retangular

Boas-vindas à calculadora da área de superfície de um prisma retangular da Omni, onde você terá a oportunidade de aprender tudo sobre o seu prisma de forma rápida e fácil. Em particular, explicaremos a você como encontrar a área de superfície de um prisma retangular. Você quer pintar um celeiro e está se perguntando quanto de tinta precisa 🇺🇸? Ou você está construindo uma piscina no seu quintal e quer saber de quantos azulejos precisa?

Não importa qual seja a pergunta, desde que ela se resuma a “qual é a área de superfície de um prisma retangular”, você veio ao lugar certo!

Antes de vermos qual é a área de superfície de um prisma retangular, devemos nos familiarizar com o prisma em si.

Imagine uma caixa. Uma caixa retangular comum, como as que você vê no supermercado, cheia de qualquer produto. Bem, isso é um prisma retangular! Ou você se lembra daqueles desenhos de casas que fazíamos na escola? Remova o telhado angular e você terá outro exemplo de prisma retangular.

Formalmente (matematicamente), um prisma retangular regular é um sólido em que todos os seis lados são retângulos perpendiculares entre si. Observe que isso, em particular, significa que há três pares de faces idênticas colocadas em lados opostos do sólido.

Além disso, como em qualquer outra definição científica, há alguns nomes sofisticados associados ao prisma. As faces inferior e superior da caixa são chamadas de bases, e cada uma das outras quatro é chamada de face lateral. Por fim, os lados de cada retângulo são chamados de arestas (novamente divididas em arestas da base e arestas laterais).

Agora chegou a hora de deixar de lado as palavras difíceis e focar em como encontrar a área de superfície de um prisma retangular.

Para saber qual é a área de superfície de um prisma retangular, precisamos conhecer todos os seus três lados. Vamos começar com a notação que usamos para eles e para os outros valores em nossa calculadora da área de superfície de um prisma retangular:

• l é o comprimento do prisma (ou o comprimento do lado da primeira base);
• w é a largura do prisma (ou o comprimento do lado da segunda base);
• h é a altura do prisma;
• A_b é a área da base do prisma;
• A_l é a área lateral do prisma;
• A é a área de superfície do prisma; e
• V é o volume do prisma.

Observe que A_b indica a área de superfície de uma única base do nosso prisma. Por outro lado, A_l representa a área lateral, ou seja, a área total das quatro faces laterais. Portanto, como o sólido tem duas bases (a inferior e a superior), a fórmula da área de superfície de um prisma retangular é a seguinte:

área de superfície = 2 × área da base + área lateral

que, em nossa notação, se traduz em

A = 2 ⋅ A_b + A_l

Lembre-se de que todas as faces em nossa calculadora são retângulos e, conforme mencionado na calculadora da área de um retângulo, elas são calculadas multiplicando os comprimentos dos lados. Agora, vamos usar essas informações para estudar a base do nosso prisma. Com nossa notação, ela é um retângulo com lados l e w, portanto, sua área é l ⋅ w. E essa é exatamente a fórmula para a área da base:

A_b = l ⋅ w

Foi muito fácil, não foi? Bem, agora vamos tentar fazer algo um pouco mais complicado e passar para a área lateral. Temos quatro faces que contribuem para esse número, e todas elas são retangulares. Além disso, entre as quatro, há dois pares de faces idênticas (as faces frontal e traseira e as faces esquerda e direita). Todas elas têm um lado igual a h, a borda lateral (ou a altura) do prisma. Além disso, o outro lado de um dos pares é igual à primeira borda da base, digamos l, e o outro é igual ao comprimento da segunda borda, que é w. Em suma, obtemos que a área lateral, ou A_l como a chamamos, é:

A_l = l ⋅ h + l ⋅ h + w ⋅ h + w ⋅ h

ou simplesmente

A_l = 2 ⋅ l ⋅ h + 2 ⋅ w ⋅ h

Observe que, juntamente com a área da base, isso nos permite traduzir a fórmula da área de superfície de um prisma retangular em:

A = 2 ⋅ A_b + A_l = 2 ⋅ l ⋅ w + 2 ⋅ l ⋅ h + 2 ⋅ w ⋅ h

Digamos que você esteja tentando revestir uma piscina e queira saber a área que precisa revestir. Se a piscina for retangular com fundo plano, então você está lidando exatamente com um prisma retangular! Vamos dar uma olhada em uma imagem para você ver isso claramente.

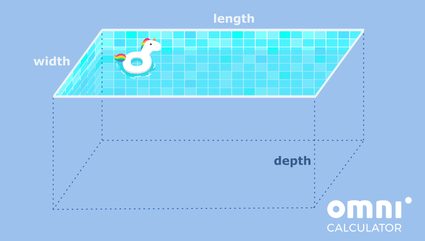
Ok, sabemos que é difícil manter seus olhos longe do unicórnio flutuante, mas voltemos ao problema em questão!

Digamos que a piscina tem um comprimento de 4 m, uma largura de 3 m e uma profundidade de 2 m. Agora que temos os números, vamos tentar colocá-los em termos da notação que usamos acima.

Em primeiro lugar, os lados da base da piscina são o comprimento e a largura, que no nosso caso são 4 m e 3 m, respectivamente. Como estamos usando l e w como bordas da base, podemos usar esses números na calculadora acima e definir l = 4 m e w = 3 m. Observe que não importa a ordem em que os colocamos; isso se traduz apenas em olhar a piscina de outro ângulo e não altera sua área de superfície.

O que nos resta é a profundidade de nossa piscina e o número h na calculadora. E é exatamente isso que devemos fazer agora: definir h = 2 m, que é a profundidade da piscina ou a altura do prisma.

E terminamos, não é mesmo? Bem, não exatamente. A área de superfície de uma calculadora de prisma retangular nos dá a resposta:

A = 2 ⋅ l ⋅ w + 2 ⋅ l ⋅ h + 2 ⋅ w ⋅ h = 2 ⋅ 4 m ⋅ 3 m + 2 ⋅ 4 m ⋅ 2 m + 2 ⋅ 3m ⋅ 2 m = 52 m²

Mas essa é a área de superfície de todo o prisma, e não queremos revestir todo o prisma. Afinal, se colocarmos revestimento na parte superior, será muito difícil entrar (ou sair), não é mesmo? Isso seria uma maldade de alto nível, ainda pior do que a remoção da escada. Se quiser saber mais sobre revestimentos e azulejos, consulte também a calculadora de azulejos 🇺🇸 da Omni.

Para encontrar a resposta correta, vamos passar para o modo avançado. Ele nos permite ver a área da base e a área lateral do sólido. Como sabemos como encontrar a área de superfície de um prisma retangular, ou seja, sabemos que:

A = 2 ⋅ A_b + A_l

só precisamos subtrair a área extra que não está sendo revestida. E essa é a parte superior. Mas a base superior é a mesma que a inferior, portanto, a área que precisamos revestir é, de fato:

área de revestimento = A - A_b

que, no nosso caso, é:

área de revestimento = 52 m² - 12 m² = 40 m²

Isso nos coloca um passo mais perto de terminar a piscina e de poder admirar seu trabalho enquanto você toma uma cerveja gelada. Dito isso, o prisma não é a única forma 3D com uma base retangular; descubra mais na calculadora da área de superfície de pirâmide retangular 🇺🇸.