Calculadora de Área de Superfície

A calculadora de área de superfície da Omni ajuda você a encontrar a área dos sólidos tridimensionais mais comuns. Se você já se perguntou como encontrar a área de uma superfície ou qual é a área de uma superfície lateral, esta calculadora está aqui para ajudá-lo. A área de superfície tem uma lista gigantesca de aplicações em campos diversos, como, por exemplo, a aerodinâmica.

Neste artigo, você pode encontrar as fórmulas para a área de superfície de uma esfera, cubo, cilindro, cone, pirâmide e prisma retangular/triangular. Também explicaremos a você como calcular a área de superfície de uma esfera como um exemplo.

A área de superfície é a área total que a superfície do objeto ocupa. Em outras palavras, é a área total da superfície de um objeto 3D.

Às vezes, a área de superfície pode ser dividida em uma soma de área(s) da base e área da superfície lateral. A superfície lateral é a área de todos os lados do objeto, excluindo a base e o topo. Essa divisão é usada para formas geométricas em que há uma distinção óbvia entre a base e a outra parte, como no caso do cilindro, cone, pirâmide ou prisma triangular, por exemplo. Essa divisão de áreas não é aplicada a sólidos para os quais não temos certeza de quais faces devem ser tratadas como bases (como em um cubo ou caixa), e não a usamos para superfícies lisas, como uma esfera.

Nossa calculadora de área de superfície pode encontrar a área de superfície de sete sólidos diferentes. A fórmula depende do tipo de sólido.

• Área de superfície de uma esfera: A = 4⋅π⋅r², em que r representa o raio da esfera.

• Área de superfície de um cubo: A = 6⋅a², em que a é o comprimento do lado (aresta).

• Área de superfície de um cilindro: A = 2⋅π⋅r² + 2⋅π⋅r⋅h, em que r é o raio e h é a altura do cilindro.

• Área de superfície de um cone: A = π⋅r² + π⋅r√(r² + h²), em que r é o raio e h é a altura do cone.

• Área de superfície de um prisma retangular: A = 2(ab + bc + ac), em que a, b e c são os comprimentos dos três lados do prisma.

• Área de superfície de um prisma triangular: A = 0,5 ⋅ √((a + b + c) ⋅ (-a + b + c) ⋅ (a - b + c) ⋅ (a + b - c)) + h ⋅ (a + b + c), em que a, b e c são os comprimentos dos três lados da base do prisma triangular e h é a altura (comprimento) do prisma.

• Área de superfície de uma pirâmide: A = l ⋅ √(l² + 4 ⋅ h²) + l², em que l é o comprimento do lado da base quadrada e h é a altura da pirâmide.

Mas de onde vêm essas fórmulas? Como você pode encontrar a área de superfície das formas 3D básicas? Continue lendo e você descobrirá!

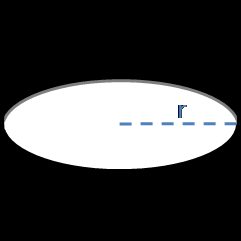
Para calcular a área de superfície de uma esfera, tudo o que você precisa saber é o raio da esfera, ou seu diâmetro.

• A = 4⋅π⋅r², em que r é o raio.

Como sabemos que o diâmetro de uma esfera é igual a dois raios d = 2⋅r, podemos usar equação também em função do diâmetro:

• A = 4⋅π⋅(d / 2)² = π⋅d² onde d é o diâmetro da esfera.

A derivação dessa fórmula de área de superfície requer integração. Se você estiver curioso, confira a demonstração.

Para descobrir a área de superfície de um cilindro, você deve ter dois valores: o raio (ou diâmetro) de uma base e a altura do cilindro. A equação geral é a usual, isto é, a área da base mais área lateral da superfície. No nosso caso, um círculo é a base.

• A = 2πr² + 2πrh

De onde vem essa fórmula? Você pode escrever a equação da área de superfície de um cilindro como:

• A = A(lateral) + 2⋅A(base)

É fácil encontrar a área da base. Basta lembrarmos da conhecida fórmula para a área de um círculo: A(base) = π ⋅ r². Mas qual seria a forma da área da superfície lateral? Tente imaginar e logo você vai reconhecer que é um retângulo! O comprimento de um lado é a altura do cilindro, e o segundo é o comprimento da circunferência do círculo desdobrada. Na calculadora de circunferência da Omni, você pode obter mais detalhes sobre essa figura geométrica.

• A(base) = π⋅r²
• A(lateral) = h⋅(2⋅π⋅r)

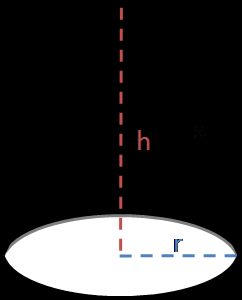
Podemos dividir a área de superfície de um cone em duas partes:

• A = A(lateral) + A(base), pois temos apenas uma base, ao contrário de um cilindro.

A base é novamente a área de um círculo A(base) = π⋅r², mas as origens da área de superfície lateral talvez não sejam tão óbvias:

• A(lateral) = π⋅r⋅√(r² + h²)

Vamos dar uma olhada nessa derivação passo a passo:

1. Role a superfície lateral para fora do plano. É um setor circular, que é a parte de um círculo com raio s (s é a altura inclinada do cone).

2. Para o círculo com raio s, o comprimento da circunferência é igual a 2⋅π⋅s. O comprimento do arco do setor é igual a 2⋅π⋅r.

3. A área de um setor, que é a superfície lateral de um cone, é dada pela fórmula:

• A(lateral) = (s⋅(comprimento do arco)) / 2 = (s⋅2⋅π⋅r) / 2 = π⋅r⋅s

  A fórmula pode ser obtida a partir de proporções, pois a razão entre as áreas das formas é a mesma que a razão entre o comprimento do arco e a circunferência:

  (área do setor) / (área do círculo grande) = (comprimento do arco) / (circunferência do círculo grande):

  (área do setor) / (π⋅s²) = (2⋅π⋅r) / (2⋅π⋅s)

  (área do setor) = (π⋅s²) ⋅ (2⋅π⋅r) / (2⋅π⋅s)

• A(lateral) = π⋅r⋅s

  Para encontrar o termo ausente dessa proporção, você também pode experimentar a calculadora de razão da Omni!

4. Normalmente, não temos o valor s dado, mas sim h, que é a altura do cone, mas isso não é um problema! Você pode transformar facilmente a fórmula usando o Teorema de Pitágoras. Caso você queira relembrar sobre esse Teorema, sugerimos que consulte outra de nossas ferramentas Omni, a calculadora do Teorema de Pitágoras.

• r² + h²= s², então, tirando a raiz quadrada, temos s = √(r² + h²)

  Assim, a fórmula da área de superfície lateral é a seguinte:

• A(lateral) = π⋅r⋅√(r² + h²)

5. Por fim, some as áreas da base e da parte lateral para encontrar a fórmula final da área de superfície de um cone:

• A = A(lateral) + A(base) = π⋅r⋅s + π⋅r² dados r e s ou
• A = π⋅r⋅√(r² + h²) + π⋅r² dados r e h.

A área de superfície de um cubo 🇺🇸 é a mais fácil que você pode imaginar. Mas, claro que a Omni também tem uma ferramenta dedicada a esse sólido, a calculadora da área de superfície de um cubo 🇺🇸. Nesse caso, como cada um dos lados é um quadrado e todo cubo tem seis faces idênticas, a área de superfície é igual a:

• A = 6⋅(área lateral)

Como a área de um quadrado é o produto do comprimento de seus lados, a fórmula final para a área da superfície de um cubo é:

• A = 6⋅l², em que l é o lado de um quadrado

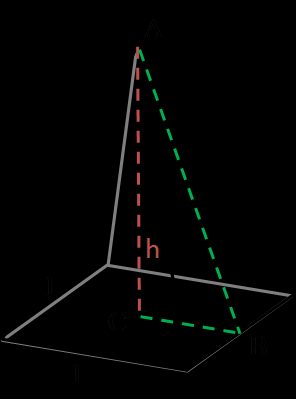
Uma pirâmide é um sólido 3D com uma base poligonal e faces laterais triangulares. Quando você ouve uma pirâmide, geralmente supõe que seja uma pirâmide quadrada regular. Mas, dependendo do formato da base, ela também pode ser uma pirâmide hexagonal ou uma pirâmide retangular. Regular significa que sua base é um polígono regular e, portanto, ela é uma pirâmide reta (vértice diretamente acima do centroide de sua base) e quadrada (tem essa forma como base). Essa é a opção que usamos como pirâmide nesta calculadora de área de superfície.

A fórmula para a área de superfície de uma pirâmide é a seguinte

• A = l⋅√(l² + 4⋅h²) + l² onde l é o lado da base e h é a altura da pirâmide

Novamente, podemos dividir a equação em:

A = A(base) + A(lateral) = A(base) + 4⋅A(face lateral)

A base tem a forma de um quadrado, portanto A(base) = l². Para calcular a área da superfície lateral, vamos começar com a área de uma face triangular:

1. Para encontrar a altura do triângulo, você pode usar a calculadora da altura de um triângulo, a calculadora de hipotenusa, ou simplesmente usar a fórmula:

   c = √(a² + b²)

2. Calcule a hipotenusa do triângulo ABC (que é, ao mesmo tempo, a altura da face triangular):

   c = √(h² + (l/2)²) = √(h² + l²/4)

3. A área de um triângulo (no nosso caso, é um triângulo isósceles) pode ser calculada com a calculadora de área de triângulo, ou ainda com a fórmula:

   A = altura ⋅ base / 2 assim

   A(face lateral) = √(h² + l²/4) ⋅ l / 2

4. Portanto, a fórmula final para a área da superfície de uma pirâmide é:

   A = l² + 4 ⋅ √(h² + l²/4) ⋅ l / 2 = l² + 2 ⋅ l ⋅ √(h² + l²/4)

   A = l² + l ⋅ √(4 ⋅ h² + l²)

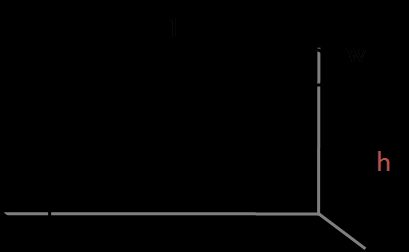
Para calcular a área de superfície de um prisma retangular, tudo o que você precisa fazer é calcular as áreas dos lados retangulares:

• A = 2 ⋅ (A1 + A2 + A3)

onde:

• A1 = l⋅w
• A2 = w⋅h
• A3 = l⋅h

Assim, a fórmula final é:

• A = 2 ⋅ (l⋅w + w⋅h + l⋅h)

Para entender de onde vem a fórmula para a área de superfície de um prisma triangular, vamos dar uma olhada nesta derivação:

1. A parte da área da superfície lateral é fácil de calcular nesse caso. Como você pode ver na figura, ela consiste em três retângulos, com um comprimento lateral em comum:

   A(lateral) = a⋅h + b⋅h + c⋅h = h⋅(a + b + c)

   De forma resumida, a fórmula fica:

   A(lateral) = h⋅P, onde P é o perímetro de uma das bases triangulares.

2. Em seguida, você deve encontrar a área de uma base triangular. Você pode fazer isso de várias maneiras, dependendo do que lhe for dado. Em nossa calculadora, implementamos o cálculo com base na fórmula de Heron, que é usada quando você tem três lados de triângulo (SSS). Consulte a calculadora da fórmula de Heron 🇺🇸, se quiser saber mais.

   A(base) = 0,25⋅√((a + b + c)⋅(-a + b + c)⋅(a - b + c)⋅(a + b - c))

3. A fórmula final para a área de superfície de um prisma triangular:

   A = A(lateral) + 2⋅A(base)

   A = h⋅(a + b + c) + 0,5⋅√((a + b + c)⋅(-a + b + c)⋅(a - b + c)⋅(a + b - c))

Você pode calcular a superfície de qualquer sólido, e não precisa ser uma forma geométrica. Por exemplo, você pode calcular inclusive a área de superfície do seu corpo! Se você estiver curioso para saber qual é a área de superfície externa de um corpo humano, confira a calculadora de ASC, também da Omni.

Se quiser encontrar a área de superfície de uma esfera, você precisa seguir estas etapas:

1. Determine o raio da esfera. Podemos supor um raio de 10 cm.

2. Insira esse valor na fórmula:

   A = 4⋅π⋅r²

3. Calcule o resultado:

   A = 4⋅π⋅10² = 1256 cm²

4. Se souber a sua área, você também pode usar uma calculadora de área de superfície on-line, como a Omni, para encontrar o raio da esfera.

As unidades de área de superfície são sempre unidades quadradas de comprimento. Por exemplo, você pode expressá-la em cm², in², ft², m², mas também em acres e hectares.

Se você quiser encontrar o volume de qualquer um desses sólidos, use nossa calculadora de volume para fazer isso.

Para converter a área da superfície de um cubo no comprimento de seu lado, siga estas etapas:

1. Anote a área de seu cubo.
2. Divida-a por seis. O resultado é a área de uma face.
3. Pegue a raiz quadrada do número da Etapa 2.
4. Esse é o comprimento de cada lado do seu cubo.

Para deduzir o raio de uma esfera a partir de sua área de superfície:

1. Escreva a área da superfície da esfera.
2. Divida-a por 4⋅π ≈ 12,566.
3. Pegue a raiz quadrada: √(Área / 4π).
4. É isso, esse é o raio! Você pode verificar o resultado usando a nossa calculadora de área de superfície.

A resposta é 50,2655 cm². Para chegar a esse resultado, lembre-se de que a fórmula da área da superfície de um cilindro é:

Área = 2⋅π⋅r(r + h)

Se você substituir r = h = 2, obteremos Área = 16π ≈ 50,2655. Lembre-se das unidades! Como r e h estão em cm, a área está em cm².