Calculadora de Arcsen

Com a calculadora de arcsen (ou calculadora do inverso da função seno) da Omni, você não terá problemas para encontrar o valor do seu ângulo. Basta inserir um valor para x (ou para o seno) e o arcsen será calculado automaticamente. A única coisa que você precisa lembrar é que o seno varia entre -1 e +1. Se você estiver se perguntando o que é arcsen ou como é o gráfico de arcsen(x), não espere mais, continue lendo e você encontrará as respostas abaixo! Também incluímos um pequeno parágrafo sobre outras relações interessantes envolvendo o arco seno, integrais e derivadas. Então, o que você está esperando?

Arcsen (ou arco seno) é o inverso da função seno. Em outras palavras, ela ajuda você a encontrar o ângulo de um triângulo que tem um valor conhecido de seno a partir da seguinte relação:

arcsen(x) = y se e somente se x = sen(y)

Como o contradomínio do seno para números reais é [-1, 1], só podemos calcular o arcsen para números nesse intervalo. Isso significa que o domínio do arcsen (para valores reais) é -1 ≤ x ≤ 1.

No entanto, como você deve (e deveria!) lembrar, o seno é uma função periódica, portanto, há vários números que têm o mesmo valor de seno. Por exemplo, sen(0) = 0, mas também sen(π) = 0, sen(2π) = 0, sen(-π) = 0 e sen(-326π) = 0. Portanto, se alguém quiser calcular arcsen(0), a resposta pode ser 0, 2π (360°) ou -π (-180°), para citar algumas opções! Todas elas estão corretas, mas normalmente fornecemos apenas um número chamado valor principal.

Arcsen(x) é a notação mais comum, pois sen^-1x pode gerar confusão (isto porque sen^-1x ≠ 1/sen(x) ). Além disso, a abreviação asin(x) é normalmente usada em linguagens de programação.

Como a função seno básica não é unívoca, seu domínio deve ser restrito para garantir que o arcsen também seja uma função. Normalmente, o domínio escolhido é -π/2 ≤ y ≤ π/2. Isso significa que o intervalo da função inversa será igual ao intervalo de uma função principal; assim, o intervalo da função arcsen é [-π/2,π/2], e o domínio do arcsen está entre [-1,1]. Abaixo, você pode encontrar o gráfico de arcsen(x), bem como alguns valores de arcsen comumente usados:

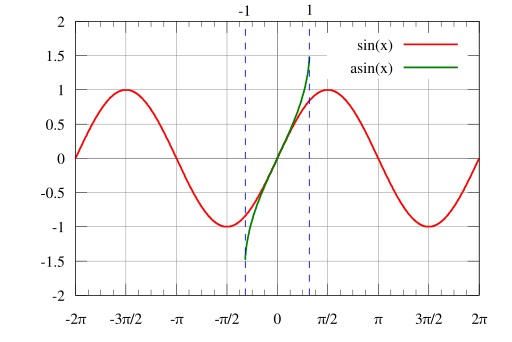
E aqui está a representação gráfica do arcsen(x):

Você está se perguntando de onde vem esse gráfico? Você pode encontrá-lo refletindo um gráfico de sen(x), entre o intervalo de [-π/2 π/2], através da reta y = x:

As relações entre as funções trigonométricas e o arcsen podem ajudar você a entender melhor esta função inversa. Um triângulo retângulo que tenha uma hipotenusa de comprimento 1 é um bom ponto de partida.

Apenas um lembrete: para um triângulo retângulo, a função seno toma o ângulo θ e retorna a razão entre o cateto oposto/hipotenusa, que é igual a x em nosso exemplo. A função inversa do seno, arcsen, tomará a razão do cateto oposto/hipotenusa(x) e retornará o ângulo θ. Assim, sabendo que, para o nosso triângulo, arcsen(x) = θ, também podemos escrever a seguintes relações:

• Seno: sen(arcsen(x)) = x
• Cosseno: cos(arcsen(x)) = √(1-x²)
• Tangente: tan(arcsen(x)) = x / √(1-x²)

Outras relações úteis com arcsen são:

• arcsen(x) = π/2 - arccos(x)
• arcsen(-x) = -arcsen(x)

Às vezes, a integral e a derivada de arcsen também são necessárias:

• integral de arcsen: ∫arcsen(x) dx = x arcsen(x) + √(1 - x²) + C
• derivada de arcsen: d/dx arcsen(x) = 1 / √(1 - x²) onde x ≠ -1, 1

Arcsen é uma função útil, por exemplo, para encontrar o ângulo de um triângulo retângulo. Se você estiver procurando os ângulos de um triângulo retângulo e souber o comprimento dos lados, o conhecido teorema de Pitágoras não será tão útil. Para encontrar os ângulos de um triângulo retângulo, você precisa aplicar o arcsen:

• para α: sen(α) = a / c, logo α = arcsen(a / c)
• para β: sen(β) = b / c, logo β = arcsen(b / c)

Então, vamos supor que você tenha dois valores dados em um triângulo retângulo, a = 6 e c = 10, e gostaríamos de encontrar o valor do ângulo α:

1. Insira o valor a partir do qual você deseja encontrar o arcsen. No nosso caso, é 6/10. Portanto, você pode inserir o valor como 0,6, mas a forma 6/10 também funcionará. Lembre-se apenas que o valor de x deve estar entre -1 e 1.
2. E... é isso! A calculadora de arcsen fez seu trabalho e você encontrou o arcsen do seu valor. Agora você sabe que arcsen(6/10) = 36,87°.

arcsen(1) = π/2 (= 90°). O arcsen é a função inversa da função sen. Como sen(π/2) = 1, arcsen(1) = π/2.

Sim, arcsen e sen⁻¹ se referem ao inverso da função sen. No entanto, arcsen é o símbolo mais comumente usado para evitar confusão na notação.

Para encontrar o arcsen de um valor x, você deve encontrar o ângulo θ em um triângulo retângulo, de modo que x seja a razão entre o cateto oposto ao ângulo θ e a hipotenusa do triângulo.

A função arcsen é uma função trigonométrica inversa. Para calcular o valor arcsen(x), siga estas etapas:

1. Encontre um gráfico da função arcsen no intervalo [-1,1].

2. Encontre o ponto na curva arcsen de modo que sua coordenada x seja igual a x.

3. Encontre a coordenada y desse ponto. O valor da coordenada y é o arcsen(x).

4. Verifique com nossa calculadora de arcsen.