Calculadora da Área de uma Esfera

Com a calculadora da área de uma esfera da Omni, você pode analisar todos os parâmetros de uma esfera que desejar, mas ela é principalmente dedicada ao cálculo da área da superfície. Como encontrar a área de uma esfera? Se você quiser apenas estimar seu valor, insira um dos valores escolhidos nos campos certos. No entanto, se você quiser aprender sobre as fórmulas da área da esfera, continue lendo.

Uma esfera é um objeto tridimensional (3D), cujos contornos e seções planas são círculos. Em outras palavras, todos os pontos da esfera estão à mesma distância de um ponto fixo (centro). Essa calculadora da área de uma esfera usa muitos valores, e a notação é a seguinte:

• r é o raio de uma esfera;
• d é o diâmetro de uma esfera;
• V é o volume de uma esfera;
• A é a área de uma esfera; e
• A / V é a proporção entre a área da superfície e volume de uma esfera.

Uma esfera é um objeto especial que tem a menor relação área de superfície/volume entre todas as outras superfícies fechadas com um determinado volume. É simplesmente como um círculo que abrange a maior área com um determinado perímetro em comparação com outras figuras planas. Se você quiser obter mais informações gerais sobre esferas, acesse a nossa calculadora de esfera 🇺🇸!

Podemos dividir qualquer esfera em duas partes iguais, que são chamadas de hemisférios. As equações que descrevem os hemisférios são muito semelhantes às que apresentamos abaixo para uma esfera completa. Você está curioso para saber quais são as propriedades dos hemisférios? Você pode conferir nossa calculadora da área de superfície de um hemisfério 🇺🇸 para saber mais sobre esse tipo de objeto!

A primeira pessoa que respondeu à pergunta sobre como encontrar a área de uma esfera foi o famoso Arquimedes. Ele descobriu que a projeção ortogonal da área lateral de um cilindro sobre a esfera mantém sua área. Observando a figura abaixo, você pode ver que ambos os objetos têm o mesmo raio r, e a altura de um cilindro é igual ao diâmetro de uma esfera d. Portanto, usando a fórmula da área da superfície de um cilindro, você obtém o seguinte:

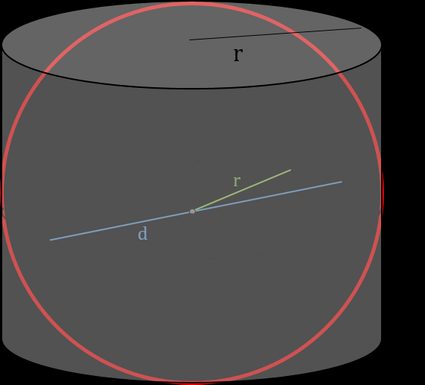
A = 2 ⋅ π ⋅ r ⋅ h;

A = 2 ⋅ π ⋅ r ⋅ d, e como d = 2 ⋅ r:

A = 2 ⋅ π ⋅ r ⋅ 2 ⋅ r; e

A = 4 ⋅ π ⋅ r²

que é a fórmula da área de uma esfera. Se você quiser ver considerações semelhantes para o raio, visite a calculadora do raio de uma esfera da Omni.

A fórmula da área de uma esfera apresentada acima foi escrita em termos de raio. No entanto, como encontrar a área de uma esfera quando você não tem o raio r, mas um valor diferente que descreve esta esfera? Primeiro, lembremos as equações para os valores possíveis:

1. Diâmetro de uma esfera: d = 2 ⋅ r;
2. Volume de uma esfera: V = 4/3 ⋅ π ⋅ r³; e
3. Relação entre área de superfície e volume de uma esfera: A / V = 3 / r.

Agora podemos tentar derivar várias fórmulas de área de superfície de uma esfera. Na calculadora da área de uma esfera, usamos quatro equações:

1. Dado o raio: A = 4 ⋅ π ⋅ r²;
2. Dado o diâmetro: A = π ⋅ d²;
3. Dado o volume: A = ³√(36 ⋅ π ⋅ V²); e
4. Dada a razão entre superfície e volume: A = 36 ⋅ π / (A/V)².

Nossa calculadora da área de uma esfera permite que você calcule a área em muitas unidades diferentes, incluindo unidades SI e imperiais. Além disso, se você quiser aprender a estimar as áreas superficiais de outras figuras, confira nossa calculadora de área da superfície, que é uma ferramenta mais geral.