Calculadora de Arredondamento Para o Inteiro Mais Próximo

Quando as casas decimais não importam, a calculadora de arredondamento para o inteiro mais próximo da Omni poder ser útil. Com a nossa simples ferramenta, você encontrará:

• Como arredondar para o número inteiro mais próximo (as regras simples);

• Os cálculos para arredondar para o número inteiro mais próximo no caso de números meio-inteiros; e

• Exemplos claros e exaustivos.

O que fazer com esse $0{,}5$ não será mais um mistério: você aprenderá a gerenciar esses números sempre confusos ou, pelo menos, descobrirá uma ferramenta que fará isso por você!

O arredondamento para o número inteiro mais próximo é uma operação matemática simples que aplicamos a números decimais. Certo, mas o que é um número decimal? Um número decimal é um número em que podemos identificar uma parte inteira ($1$, $2$, $3$, etc.) e um excesso (parte decimal). Separamos essas duas quantidades com o separador decimal:

No exemplo acima, a parte inteira é representada pela cor vermelha e o excesso fracionário é representado pela cor azul. Muitas vezes precisamos nos livrar da parte decimal (digamos que não precisamos dela ou, como aprendemos na calculadora de algarismos significativos, essa precisão seria muito alta). O resultado dos cálculos para arredondar para o número inteiro mais próximo é um número inteiro, como você pode entender pelo nome. Mas quais são as regras que usamos para fazer isso?

As regras a seguir se aplicam a todo intervalo entre dois pares de inteiros contíguos (por exemplo, $1$-$2$, $10$-$11$, $-9$-$-8$, etc.). Em qualquer intervalo desse tipo, você pode encontrar números decimais infinitos. Para a maioria deles, os cálculos para arredondar para o número inteiro mais próximo são bastante simples. Considere o número inteiro genérico $i$. Aqui estão as possíveis situações que você pode encontrar ao considerar o número decimal $n$:

• Para $n = i,\!0$, arredondamos para $i$;

• Para $n\ \text{\textgreater}\ i,\!0$ e $n\ \text{\textless}\ i,\!5$, arredondamos para $i$ (você pode simplesmente apagar a parte decimal);

• Para $n=i,\!5$, verifique a próxima seção;

• Para $n\ \text{\textgreater}\ i,\!5$ e $n\ \text{\textless}\ i+1,\!0$ (onde $i+1$ é o número inteiro superior mais próximo), arredondamos para $i+1$; e

• Para $n=i+1,\!0$, arredondamos para $i+1$.

Você pode ver uma simetria, com comportamentos semelhantes separados pelo valor $i,\!5$. Antes de verificar o que fazer no caso de números meio-inteiros, podemos ver alguns exemplos das situações que listamos acima.

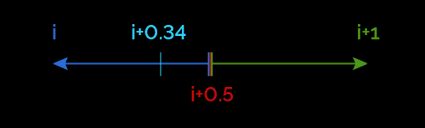
Pegue $4,\!8$. Como ele está na segunda metade da integral, arredondamos para $4+1 = 5$. E quanto a $5,\!0$, então? Basta você cortar o $,\!0$: $5{,}0\rightarrow 5$.

Consideremos a outra metade do intervalo: no caso de $1,\!3$, arredondamos para $1$. E quanto às partes decimais mais longas? Consideremos pi, $3,\! 141592653589$. Sim, como você pode ver, a parte decimal cai na primeira metade, de $3,\!0$ e $3,\!5$: arredondar pi para o número inteiro mais próximo retorna $3$, como muitos irão concordar!

Para números negativos, siga as mesmas regras!

O que acontece no caso de meio-inteiros? Todo número decimal que termina com $0,\!5$ tem a mesma “distância” dos dois inteiros que definem o intervalo. Então, como arredondamos para o número inteiro mais próximo? Usamos uma convenção chamada arredondamento pela metade, em que $0,\!5$ vai para cima:

Observe que essa operação retorna resultados diferentes para números negativos e positivos:

Enquanto isso:

O arredondamento da metade para cima não é a única maneira de arredondar números meio-inteiros para o inteiro mais próximo.

• Ao arredondar metade para baixo, você retorna o menor número inteiro entre os extremos: $4,\!5\rightarrow4$, e $-4,\!5\rightarrow-5$.

• O arredondamento da metade par retorna resultados alternados:

Observe que essa maneira de calcular o arredondamento para o número inteiro mais próximo sempre retorna um número par.

Observe, também, que você pode expressar a política da metade para cima usando a função “teto”. A função “piso”, nos dá outra política de arredondamento. Dêmos uma olhada!

Piso e teto são um par de funções matemáticas específicas que retornam, respectivamente, o menor número inteiro mais próximo e o maior número inteiro mais próximo:

E:

Usando essas funções, definimos:

• O arredondamento metade teto, que retorna o teto de $i,\!05$: $4,\!5\rightarrow5$, e $-4,\!5\rightarrow -4$.

• O arredondamento metade piso, em que você aplica a função "piso", obtendo sempre o menor número inteiro: $4,\!5\rightarrow4$, e $-4,\!5\rightarrow-5$.

Uma última opção é a chamada “longe de $0$”. Nesse caso, você arredonda os meios inteiros para o número inteiro que está no lado oposto de $0$ na reta numérica: $4,\!5\rightarrow5$, e $-4,\!5\rightarrow-5$.

A utilidade de nossa ferramenta é simples: você entra com o número e nós o arredondamos para o número inteiro mais próximo, de acordo com as regras descritas neste artigo.

Se você quiser acessar opções mais avançadas, clique em Modo Avançado. Lá você encontrará outras técnicas de arredondamento (por exemplo, a potência desejada de dez) ou arredondamento para números meio inteiros.

O arredondamento para o número inteiro mais próximo é apenas uma das muitas maneiras de arredondar um número. A Omni cuidou disso! Tente nossas outras ferramentas de arredondamento:

• Calculadora de arredondamento (para uma ferramenta geral que cubra todas as suas necessidades);
• Calculadora de arredondamento para a dezena mais próxima;
• Calculadora de arredondamento para o décimo mais próximo](calc:6134);
• Calculadora de arredondamento para a centena mais próxima;
• Calculadora de arredondamento para o centésimo mais próximo;
• Calculadora de arredondamento para o milhar mais próximo;
• Calculadora de arredondamento para o milésimo mais próximo;
• Calculadora de arredondamento para o dólar mais próximo 🇺🇸;
• Calculadora de arredondamento para o centavo mais próximo 🇺🇸; e
• Calculadora de arredondamento de centavos 🇺🇸.

Para arredondar um número decimal para o número inteiro mais próximo, dê uma olhada em sua parte fracionária:

• Se a parte decimal estiver entre ,0 (incluído) e 0,5 (excluído), arredonde para a parte inteira.

• Se a parte decimal estiver entre ,5 (excluída) e ,0 (excluída), arredonde o número inteiro para a parte +1.

• Se a parte decimal for ,5 (meio inteiro), sempre arredonde para o maior inteiro mais próximo.

Para arredondar 4,5, siga os passos a seguir:

1. Escolha o tipo de arredondamento: o padrão é chamado “metade para cima”.

2. Adicione 0,5 ao número:

   4,5 + 0,5 = 5,0

3. Arredonde de acordo com os procedimentos padrão: o resultado é 5.

Não! Antes de arredondar um número meio inteiro, você deve ter certeza sobre o tipo de arredondamento a ser usado. Aqui estão os mais comumente usados:

• Metade para cima (também conhecido como metade teto): você sempre arredonda os meios inteiros para o maior inteiro mais próximo;

• Metade par: você sempre arredonda para o número par mais próximo;

• Metade para baixo: você sempre arredonda para o número mais próximo de 0;

• Metade piso: o resultado é sempre o menor número inteiro vizinho; e

• Longe de 0: você arredonda para o número que está longe de 0 na reta numérica.

Os números negativos seguem as mesmas regras definidas para os números positivos quando você os arredonda para o número inteiro mais próximo, com exceção dos números meio inteiros.

No caso de números meio inteiros, você deve escolher uma convenção para arredondar para o número mais próximo. Na convenção de metade para cima, você deve tratar 0,5 como uma parte fracionária “maior” e arredondar o número para o número inteiro à direita na reta numérica.