Calculadora de Mudança de Fase

Boas-vindas à calculadora de mudança de fase da Omni, onde estudaremos as funções trigonométricas e como calcular suas mudanças de fase. Na verdade, abordaremos mais do que isso: também explicaremos como encontrar a amplitude e como encontrar o período de uma oscilação. Podemos verificar que uma enorme classe de funções se comporta praticamente da mesma forma, e as diferenças se resumem em especificar os valores mencionados acima: a amplitude, o período e a mudança de fase. Podemos calcular também o deslocamento vertical de uma função comparado às funções trigonométricas seno e cosseno.

Como mencionamos acima, nos concentraremos aqui nas funções trigonométricas: mais especificamente no seno e no cosseno. No entanto, é importante lembrar que muitos dos conceitos aqui abordados possuem aplicações em funções mais gerais, como, por exemplo, a translação horizontal ou deslocamento vertical.

Em primeiro lugar, vamos ver um gráfico que mostra a amplitude, o período, a mudança de fase e o deslocamento vertical (observe que a mesma imagem aparece na parte superior da calculadora de mudança de fase da Omni).

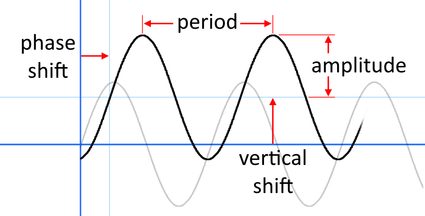
Podemos escrever essas funções com a fórmula (às vezes chamada de equação de mudança de fase ou fórmula de mudança de fase):

ou

onde $A$, $B$, $C$, $D$ são números reais arbitrários. Além disso, $A$ e $B$ são diferentes de zero (caso contrário, f(x) não seria uma função trigonométrica). Esses quatro parâmetros determinam a amplitude, o período, a mudança de fase e o deslocamento vertical da função, respectivamente. A imagem acima ilustra como eles afetam o gráfico da função. Ainda assim, para que você entenda melhor os elementos presentes nesta figura, faremos uma breve descrição de cada um deles.

1. A amplitude é a medida da variação da função a partir da linha central do gráfico. Para um seno ou cosseno simples, seu valor é $1$, pois a linha central está em $0$ e os valores da função variam de $-1$ a $1$.

2. O período é o comprimento no eixo horizontal, após o qual a função começa a se repetir. Em outras palavras, o gráfico como um todo é formado por cópias da função dentro do intervalo do período coladas uma após a outra. Para um seno ou cosseno simples, o período é igual a $2\pi$, pois $\mathrm{sen}(0) = \mathrm{sen}(2\pi) = \mathrm{sen}(4\pi) = ...$

3. A mudança de fase (também chamada de deslocamento horizontal ou translação horizontal) descreve a distância horizontal em que o gráfico foi movido em relação ao seno ou cosseno regular. Dessa forma, o valor é igual a $0$ se você tiver as duas funções sobrepostas ou em fase.

4. O deslocamento vertical (também chamado de translação vertical) descreve o quanto o gráfico foi deslocado verticalmente em relação ao seno ou cosseno regular. Em outras palavras, é o deslocamento de fase em relação à direção perpendicular. Em particular, o valor é novamente igual a $0$ se tivermos as duas funções inalteradas.

Muito bem, aprendemos o que é a mudança de fase, bem como os três valores que a acompanham. As seções abaixo descrevem como calcular cada um deles com base na notação da fórmula de mudança de fase acima. Primeiro, mostramos como encontrar a amplitude.

O conceito que introduzimos é muito difundido no estudo de movimentos oscilatórios e harmônicos. Essas oscilações são excelentes aplicações das funções trigonométricas. Você pode descobrir a conexão na calculadora de trigonometria da Omni ou aprender mais sobre as várias funções que aparecem quando você analisa um pêndulo na calculadora de funções trigonométricas 🇺🇸 ou nas nossas ferramentas mais específicas: a calculadora de cosseno 🇺🇸 e a calculadora de seno 🇺🇸!

Sabemos que as funções seno e cosseno têm valores que variam de $-1$ a $1$. Além disso, esse simples fato não muda se substituirmos $\mathrm{sen}(x)$ ou $\cos(x)$ por $\mathrm{sen}(Bx - C)$ ou $\cos(Bx - C)$ considerando $B$ diferente de zero e $C$ arbitrário. Na verdade, isso ocorre porque a função $f(x) = Bx - C$ é do tipo bijetora (ou seja, uma correspondência de um para um) no espaço dos números reais.

Vamos ver o que acontece se adicionarmos $D$, ou seja, se tivermos $\mathrm{sen}(Bx - C) + D$ ou $\cos(Bx - C) + D$. Como vimos, anteriormente a função variava entre $-1$ e $1$, já neste caso, os valores máximo e mínimo passam a variar entre $-1 + D$ e $1 + D$ (consulte a seção "Como encontrar o deslocamento vertical" para comparação). Isso significa que metade do gráfico da função estará acima e metade estará abaixo de $D$, contudo, a amplitude ainda continua igual a $1$.

Portanto, a única coisa que pode afetar a amplitude nas fórmulas de mudança de fase $A\cdot\mathrm{sen}(Bx - C) + D$ e $A\cdot\cos(Bx - C) + D$ é o valor do parâmetro $A$. Uma vez que $\mathrm{sen}(Bx - C)$ e $\cos(Bx - C)$ variam entre $-1$ e $1$, ao multiplicarmos estas funções por $A$, o intervalo será alterado para $-1\cdot A = -A$ e $1 \cdot A = A$.

Consequentemente, a amplitude das equações de mudança de fase $A \cdot\mathrm{sen}(Bx - C) + D$ e $A \cdot\cos(Bx - C) + D$ é simplesmente igual a $A$.

Lembre-se de que as funções seno e cosseno têm períodos iguais a $2\pi$, ou seja, temos $\mathrm{sen}(x + 2\pi) = \sin(x)$ e $cos(x + 2\pi) = cos(x)$ para qualquer $x$. Deste modo, ficamos com:

e

Portanto, vemos que $A$ e $D$ não têm efeito sobre o período. Na verdade, tudo se resume ao que acontece nos argumentos das funções trigonométricas. Além disso, veja que:

e

As equações acima mostram que $C$ também não altera o período das funções trigonométricas. Portanto, após descartarmos as contribuições desses três parâmetros, nos resta considerar que o quarto é o responsável por alterar o período, ou seja, a constante $B$.

Vejamos como $B$ altera o período das funções trigonométricas $A \cdot \mathrm{sen}(Bx - C) + D$ e $A \cdot \cos(Bx - C) + D$:

Portanto, a cada $2\pi/B$ adicionado ao argumento $x$, voltamos ao mesmo ponto, e a função se repete (o mesmo ocorre com a função cosseno).

Resumindo, o período de uma equação de mudança de fase é igual a $2\pi/B$.

No dia a dia, quando buscamos alguma informação sobre ondas, geralmente elas são descritas a partir da frequência ao invés do período, contudo, estas grandezas estão conectadas. Descubra como na calculadora de frequência da Omni.

Por definição, a mudança de fase descreve o deslocamento horizontal da função em relação à forma regular do $\mathrm{sen}(x)$ ou do $\cos(x)$. Assim, se as funções estiveram em fase, esse parâmetro é igual a $0$. Observe que ao compararmos os gráficos das funções seno e cosseno

constatamos que podemos obter uma a partir da outra usando um deslocamento horizontal ou uma mudança da fase. Matematicamente, as mudanças de fase responsáveis por cada transformação podem ser escritas como:

e

O exemplo acima sugere onde devemos procurar pelos valores responsáveis pela mudança de fase nas equações $A \cdot\sin(Bx - C) + D$ e $A \cdot\cos(Bx - C) + D$. Ao contrário da amplitude e do período, vemos que no caso da mudança de fase precisaremos de duas das quatro constantes.

Em geral, (ou seja, não apenas em equações de mudança de fase), obtemos o deslocamento horizontal de uma função arbitrária $f(x)$ a partir da relação $f(x - a)$: a qual é equivalente a um deslocamento do gráfico de $a$ para a direita. Em outras palavras, substituímos cada ocorrência de $x$ por $x - a$ na fórmula para $f(x)$. Por exemplo, no caso do $\mathrm{sen}(x)$, obtemos $\mathrm{sen}(x - a)$, já para $\cos(3x + 1)$, ficamos com:

Em outras palavras, não podemos nos esquecer das constantes que multiplicam $x$.

Em nosso caso, a fórmula de mudança de fase fornece:

que equivale a um deslocamento de fase de $C/B$ (para a direita) da função $A \cdot\mathrm{sen}(Bx)$. Obviamente, também podemos repetir o procedimento acima para a função cosseno.

Em resumo, para calcular a mudança de fase de $f(x)$, você precisa encontrar $C/B$.

Esse é o parâmetro mais fácil, especialmente agora que vimos como obter a mudança de fase, a amplitude e o período. Vamos nos basear no que aprendemos até agora.

Sabemos que nas fórmulas de mudança de fase $A \cdot\mathrm{sen}(Bx - C) + D$ e $A \cdot\cos(Bx - C) + D$, o parâmetro $A$ determina os valores máximo e mínimo da sua oscilação. A constante $B$ especifica onde o gráfico irá se repetir e com que frequência. Além disso, combinando essa constante com o parâmetro $C$, podemos verificar se a função foi deslocada para a direita ou para a esquerda.

Obviamente, a translação horizontal não afeta o deslocamento vertical, afinal, estas são duas direções perpendiculares. Por outro lado, a amplitude apenas nos diz até onde o gráfico chega verticalmente, mas não o desloca. Em suma, só nos resta um parâmetro: o $D$.

O parâmetro $D$ nas equações de mudança de fase é precisamente o responsável pelo deslocamento vertical. Ele determina o intervalo da função, ou seja, o quanto deslocamos verticalmente a função em relação às funções trigonométricas originais.

Isso conclui nossas abordagens teóricas. É hora de você ver como calcular o deslocamento de fase em um exemplo. Mostraremos a você como encontrar o período, a amplitude e o deslocamento vertical.

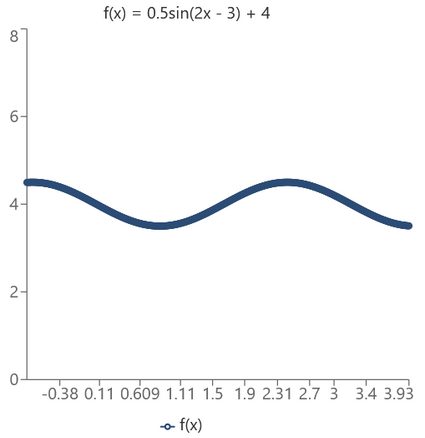
Vamos ver como encontrar a amplitude, o período, a mudança de fase e o deslocamento vertical da função $f(x) = 0{,}5 \cdot\mathrm{sen}(2x - 3) + 4$. Em primeiro lugar, deixaremos que a calculadora de deslocamento de fase do Omni faça o trabalho por você.

Na parte superior da nossa ferramenta, precisamos escolher a função que aparece em nossa fórmula. No nosso caso, escolhemos a opção "seno". Esse procedimento acionará uma representação simbólica dessa equação de mudança de fase: $f(x) = A \cdot\mathrm{sen}(Bx - C) + D$. Considerando a função que desejamos analisar, inclua os seguintes dados na calculadora:

Observe como, mesmo antes de inserirmos os valores, a calculadora de mudança de fase exibe o gráfico da função $\mathrm{sen}(x)$. Isso ocorre porque a ferramenta está padronizada para ler automaticamente os seguintes valores para os parâmetros: $A = 1$, $B = 1$, $C = 0$ e $D = 0$. Resultando na função:

No momento em que fornecemos o último parâmetro, o gráfico da função aparece abaixo junto com os valores para a amplitude, o período, a mudança de fase e o deslocamento vertical. Além disso, observe que, se necessário, você pode entrar no Modo Avançado da calculadora para encontrar o valor da função em qualquer ponto $x_0$.

Agora vamos explicar como encontrar o deslocamento de fase e todos os outros valores por conta própria. Para isso, basta relembrar as quatro seções discutidas anteriormente. Assim, neste caso teremos que:

• A amplitude é $A = 0{,}5$;
• O período é $2\pi / B = 2\pi / 2 = \pi$;
• A mudança de fase é $C / B = 3 / 2 = 1{,}5$; e
• O deslocamento vertical é $D = 4$.

Desta forma, o gráfico tem a seguinte representação:

Não foi tão difícil assim, não é mesmo? Continue explorando a calculadora de mudança de fase para ver como diferentes parâmetros afetam o gráfico.

Para calcular a mudança de fase de uma função A⋅sen(Bx - C) + D ou A⋅cos(Bx - C) + D, você precisa:

1. Determinar B.
2. Determinar C.
3. Dividir C/B.
4. Lembre-se de que, se o resultado for:
   • Positivo, o gráfico será deslocado para a direita.
   • Negativo, o gráfico será deslocado para a esquerda.
5. É isso, você encontrou a mudança de fase!

Para encontrar a mudança de fase a partir de um gráfico, você precisa:

1. Determinar se é uma função seno ou cosseno deslocada.
2. Analisar o gráfico à direita do eixo vertical.
3. Encontrar o primeiro:
   • Pico ou Crista se o parâmetro no argumento da função for positivo; ou
   • Vale se o parâmetro no argumento da função for negativo.
4. Calcular a distância do eixo vertical até esse ponto.
5. Se a função for um seno, subtraia π/2 ou 3 π/2 dessa distância caso você tenha uma crista ou um vale, respectivamente.
6. Parabéns, você encontrou a mudança de fase a partir de um gráfico!

Você pode encontrar a amplitude, o período e a mudança de fase de uma função da forma A⋅sen(Bx - C) + D ou A⋅cos(Bx - C) + D considerando que:

• A amplitude é igual a A;
• O período é igual a 2π / B; e
• A mudança de fase é igual a C / B.

Para fazer o gráfico de funções trigonométricas com mudança de fase, você precisa:

1. Determinar qual é a função trigonométrica.
2. Focar na origem ou no ponto (0,0) do plano.
3. Se a mudança de fase for:
   • Positiva, mova a função para a direita da origem.
   • Negativa, mova a função para a esquerda da origem.
4. Deslocar a função conforme o valor da mudança de fase.
5. O ponto após o deslocamento será a sua nova origem.
6. Desenhar o gráfico da função não deslocada considerando a origem dela em (0,0).
7. Parabéns, você fez o gráfico da função trigonométrica com deslocamento de fase!

Quando se trata de funções trigonométricas, sim. Normalmente, reservamos o termo "deslocamento de fase" para as funções trigonométricas. Em outras palavras, podemos ter um deslocamento horizontal de qualquer gráfico ou função. Ainda assim, quando se trata, de uma função trigonométrica, podemos chamar esse deslocamento horizontal de deslocamento de fase.