Einheitskreis Rechner

Willkommen beim Einheitskreis-Rechner ⭕. Unser Tool hilft dir, die Koordinaten eines beliebigen Punktes auf dem Einheitskreis zu bestimmen. Gib einfach den Winkel ∡ ein, und wir zeigen dir den Sinus und Kosinus deines Winkels.

Wenn du dir nicht sicher bist, was ein Einheitskreis ist, scrolle nach unten und du wirst die Antwort finden. Die Einheitskreis-Tabelle und eine Erklärung, wie man den Tangens des Einheitskreises, den Sinus und den Kosinus findet, findest du hier ebenfalls. Also warte nicht länger – lies in diesem grundlegenden Trigonometrie Rechner weiter!

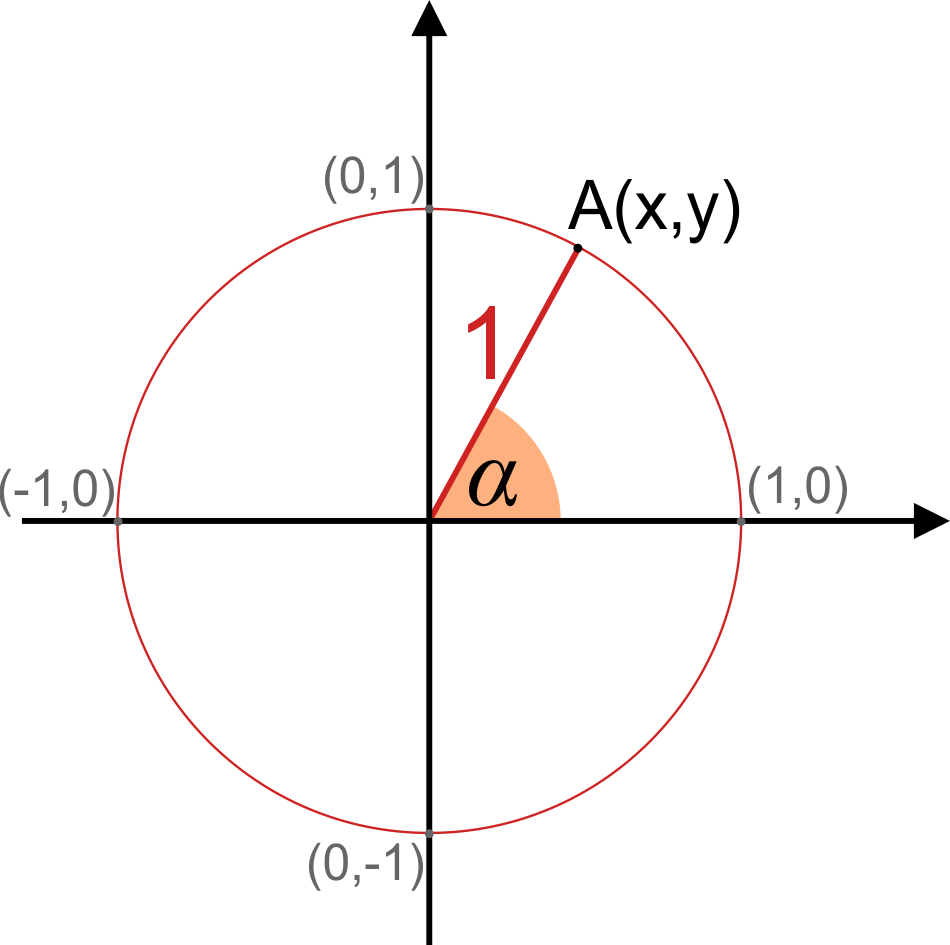
Ein Einheitskreis ist ein Kreis mit einem Radius von 1 (Einheitsradius). In den meisten Fällen hat er seinen Mittelpunkt im Punkt $(0,0)$, dem Ursprung des Koordinatensystems.

Der Einheitskreis ist ein sehr nützliches Konzept, wenn du Trigonometrie und Winkelumrechnung lernst.

Da du nun weißt, was ein Einheitskreis ist, kommen wir zu den Beziehungen im Einheitskreis.

Warum ist der Einheitskreis in der Trigonometrie so nützlich?

Kurz gesagt:

Beziehungen des Einheitskreises für Sinus und Kosinus:

• Sinus ist die y-Koordinate; und
• Kosinus ist die x-Koordinate.

Ausführliche Erklärung:

Nehmen wir einen beliebigen Punkt A auf dem Umfang des Einheitskreises.

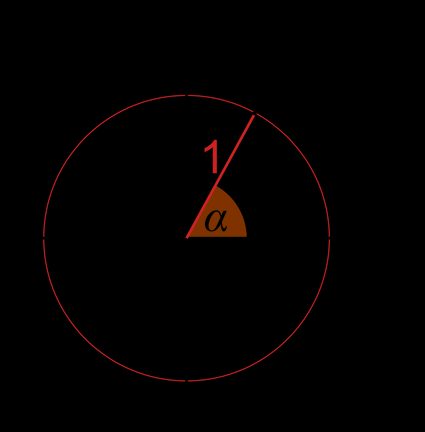
• Die Koordinaten dieses Punktes sind $x$ und $y$. Da es sich um einen Einheitskreis handelt, beträgt der Radius r $1$ (eine Entfernung zwischen Punkt $P$ und dem Mittelpunkt des Kreises).

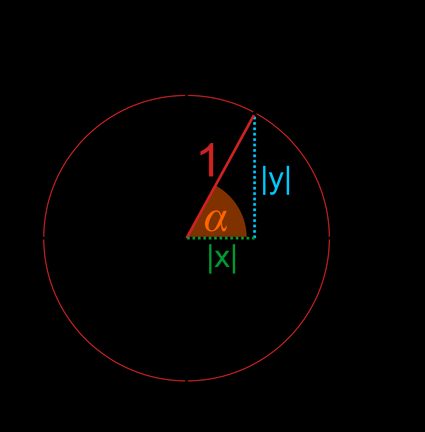
• Wenn wir den Radius auf die x- und y-Achse projizieren, erhalten wir ein rechtwinkliges Dreieck, bei dem $|x|$ und $|y|$ die Längen der Schenkel sind und die Hypotenuse $1$ ist.

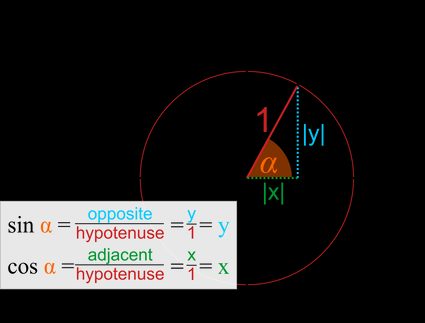
• Wie in jedem rechtwinkligen Dreieck kannst du die Werte der trigonometrischen Funktionen bestimmen, indem du die Seitenverhältnisse ermittelst:

Mit anderen Worten: Der Sinus ist die y-Koordinate:

Und der Kosinus ist die x-Koordinate.

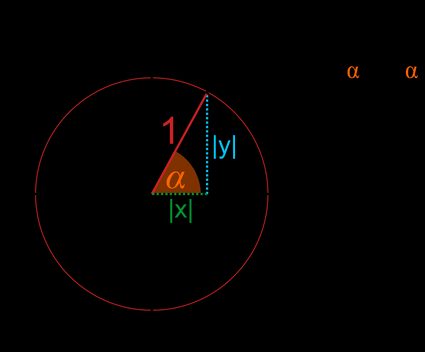
Die Gleichung des Einheitskreises, die sich direkt aus dem Satz des Pythagoras ergibt, sieht folgendermaßen aus:

Oder, analog dazu:

Diese enge Verbindung zwischen Trigonometrie und Dreiecken kann nicht überraschender sein! Mehr über diese wichtigen Konzepte erfährst du in Omni's Rechtwinkliges Dreieck Rechner.

Du kannst den Tangens des Einheitskreises direkt ermitteln, wenn du dich an die Definition des Tangens erinnerst:

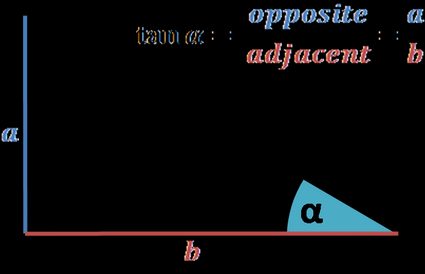
Das Verhältnis der gegenüberliegenden und der angrenzenden Seiten zu einem Winkel in einem rechtwinkligen Dreieck.

Wie wir im vorigen Absatz gelernt haben, $\sin(\alpha) = y$ und $\cos(\alpha) = x$, also:

Wir können den Tangens des Winkels auch als seinen Sinus geteilt durch seinen Kosinus definieren:

Das führt natürlich zu demselben Ergebnis.

Eine andere Methode ist natürlich die Verwendung unseres Einheitskreis-Rechners. 😁

Aber was ist, wenn du dich mit diesem Wert nicht zufriedengibst und du den Tangens auf deinem Einheitskreis** sehen möchtest?

Das ist etwas kniffliger als den Sinus und Kosinus zu bestimmen – welche einfach die Koordinaten sind. Es gibt zwei Möglichkeiten, den Tangens des Einheitskreises darzustellen:

1. Methode:

1. Erstelle eine Tangente am Punkt $A$.
2. Sie schneidet die x-Achse im Punkt $B$.
3. Die Länge des Segments $\bar{AB}$ ist der Wert des Tangens

2. Methode:

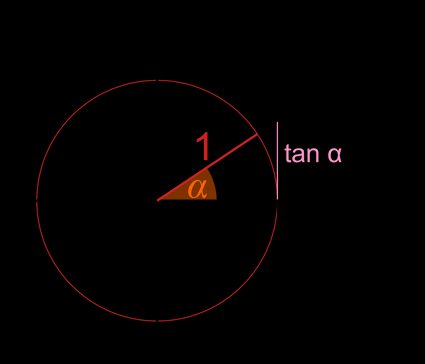
1. Zeichne eine Gerade $x = 1$.
2. Verlängere die Gerade um den Radius.
3. Benenne den Schnittpunkt dieser beiden Geraden als Punkt $C$.
4. Der Tangens, $\tan(\alpha)$, ist die y-Koordinate des Punktes $C$.

Bei beiden Methoden haben wir rechtwinklige Dreiecke erstellt, deren angrenzende Seite gleich 1 ist 😎

Sinus, Kosinus und Tangens sind nicht die einzigen Funktionen, die du auf dem Einheitskreis konstruieren kannst. Neben der Tangens-Kofunktion – dem Kotangens – kannst du auch andere weniger bekannte Funktionen darstellen, z. B. den Sekans, Kosekans und den Versinus:

Das Konzept des Einheitskreises ist sehr wichtig, weil du damit den Sinus und Kosinus eines beliebigen Winkels bestimmen kannst. Im Folgenden stellen wir einige häufig vorkommende Winkel in der Einheitskreis-Tabelle vor:

Ein Beispiel: Wie bestimmt man $\sin(150\degree)$?

1. Suche nach dem Winkel $150\degree$.
2. Wie wir bereits gelernt haben, ist der Sinus eine y-Koordinate, also nehmen wir die zweite Koordinate vom entsprechenden Punkt auf dem Einheitskreis:

Alternativ kannst du auch den Winkel 150° in unseren Einheitskreis-Rechner eingeben. Der Rechner zeigt dir den $\sin(150\degree)$ Wert deiner y-Koordinate sowie den Kosinus, den Tangens und das Diagramm des Einheitskreises an.

Nun, es kommt darauf an, was du dir merken möchtest 🙃. Es gibt zwei Dinge, die du dir merken musst, wenn es um den Einheitskreis geht:

1. Winkelumrechnung, also wie man zwischen einem Winkel in Grad und einem in Form von $\pi$ (Einheitskreis im Bogenmaß) wechselt; und

2. Die trigonometrischen Funktionen der gängigen Winkel.

Beginnen wir mit dem einfacheren ersten Teil. Die wichtigsten Winkel sind die, die du immer wieder benutzen wirst:

• $30\degree = \pi/6$;
• $45\degree = \pi/4$;
• $60\degree = \pi/3$;
• $90\degree = \pi/2$; und
• Voller Winkel, $360\degree = 2\pi$.

Da diese Winkel sehr häufig vorkommen, versuche, sie auswendig zu lernen ❤️. Für alle anderen Winkel kannst du die Formel zur Winkelumrechnung verwenden:

Die Umrechnung von Bogenmaß des Einheitskreises in Grad sollte kein Problem mehr sein! 💪

Der andere Teil – das Auswendiglernen der gesamten Einheitskreis-Tabelle mit Sinus- und Kosinuswerten – ist ein etwas längerer Prozess. Wir werden ihn hier nicht beschreiben, aber du kannst dir diese Tabelle als Lernhilfe oder diese WikiHow-Seite ansehen. Wenn du lieber Videos schaust 🖥️, statt zu lesen 📘, schau dir dieses Video an, in dem erklärt wird, wie man sich den Einheitskreis merken kann:

• Sinus-/Kosinusfunktion verdeutlicht mit Einheitskreis, Kreisfunktionen | Mathe by Daniel Jung.

Auch diese Tabelle mit den gebräuchlichsten Winkeln kann dir nützlich sein:

Und wenn alle Methoden versagen, kannst du unseren Einheitskreis-Rechner benutzen – er ist für immer für dich da ❤️. Hoffentlich hilft dir dieses Tool, die Werte des Einheitskreises besser zu verstehen und auswendig zu lernen!

tan 30° = 1/√3. Um diese Antwort auf dem Einheitskreis zu finden, müssen wir zunächst die Werte für sin und cos als y-Koordinate bzw. x-Koordinate bestimmen: sin 30° = 1/2 und cos 30° = √3/2. Verwende nun die Formel. Erinnere dich daran, dass tan 30° = sin 30° / cos 30° = (1/2) / (√3/2) = 1/√3, bereits gesagt. Siehst du, wie einfach das ist?

Bestimme die Kosekante von θ auf dem Einheitskreis:

1. Zeichne vom Mittelpunkt des Kreises aus den Radius, der dem Winkel θ entspricht.
2. Zeichne Tangenten an den Kreis in den Punkten (0,1) und (0,-1).
3. Verlängere den Radius aus Schritt 1 so, dass er eine dieser Tangenten schneidet.
4. Die Entfernung vom Mittelpunkt zum Schnittpunkt aus Schritt 3 ist der Kosekans des Winkels θ.
5. Wenn es keinen Schnittpunkt gibt, ist der Kosekans von θ undefiniert (das passiert, wenn sin θ = 0).

Da der Arkussinus die Umkehrung der Sinusfunktion ist, ist die Bestimmung von Arkussinus(1/2) gleichbedeutend mit der Bestimmung eines Winkels, dessen Sinus gleich 1/2 ist. Auf dem Einheitskreis sind die Werte des Sinus die y-Koordinaten der Punkte auf dem Kreis. Betrachtet man den Einheitskreis, so stellt man fest, dass die y-Koordinate für den Winkel π/6 beträgt 1/2 ist, d. h. 30°.