Calcolatore per la Circonferenza Goniometrica

Q: Che cos'è la circonferenza goniometrica?

La circonferenza goniometrica è un cerchio con raggio 1 1 1 (raggio unitario). Nella maggior parte dei casi, è centrato nel punto ( 0 , 0 ) (0,0) ( 0 , 0 ) , l'origine del sistema di coordinate. La circonferenza goniometrica è un concetto molto utile per imparare la trigonometria e la conversione degli angoli.

Q: Qual è la tangente di 30 gradi sulla circonferenza goniometrica?

tan 30° = 1/√3 . Per trovare questa risposta sulla circonferenza goniometrica, o circonferenza trigonometrica, iniziamo trovando i valori di sin e cos come coordinate y e x, rispettivamente: sin 30° = 1/2 e cos 30° = √3/2 . Ora usa la formula. Ricorda che tan 30° = sin 30° / cos 30° = (1/2) / (√3/2) = 1/√3 , come indicato. Vedi come è facile?

Q: Come si trova l'arcoseno di 1/2 sulla circonferenza goniometrica?

Poiché l'arcoseno è la funzione inversa della funzione seno , trovare arcsin(1/2) equivale a trovare un angolo il cui seno è uguale a 1/2 . Sulla circonferenza goniometrica, chiamata anche circonferenza trigonometrica, i valori del seno sono le coordinate y dei punti sul cerchio. Osservando la circonferenza goniometrica, vediamo che la coordinata y è uguale a 1/2 per l'angolo π/6 , cioè 30° .

Creatori

Dott. Hanna Pamuła, Ph.D.

Hanna PamułaPhD

Website

Research Gate

Hanna (Hania) Pamuła holds a Ph.D. in Bioacoustics / Mechanical Engineering, obtained at AGH University of Science and Technology. She has participated in research work in labs in France and the UK and presented papers at several international conferences. Hania has a penchant for photography and graphic design. When not in the office, she’s probably traveling, hiking, or out in the field, watching birds and recording their calls. See full profile

Check our editorial policy

Traduttori

Agata Flak

Agata is an aspiring translator and interpreter with a passion for foreign languages and linguistics. She holds a Bachelor’s degree in French and Italian Studies from the University of Manchester. She spent a year studying translation and interpreting in Mons, Belgium. She is currently pursuing her Master’s degree in Translation Studies at the Jagiellonian University in Cracow, specializing in conference interpreting. In her free time, she likes petting her dog and engaging in physical training. See full profile

Check our editorial policy

e Rangsimatiti Binda Saichompoo

Rangsimatiti Binda Saichompoo

Environmental matters and supporting sustainability are always the most important aspects of Kat’s goals. Hence, Kat directed her education towards biomaterials, sustainability, and bioeconomy. Despite this major path, psychology, language, and culture are also her other strong fields of interest! Thanks to her Erasmus Joint Master’s degree, learning and adapting to new cultures is a piece of cake. See full profile

Check our editorial policy

Revisori

Dott. Dominik Czernia, Ph.D.

Dominik CzerniaPhD, Institute of Nuclear Physics PAN

Website

Research Gate

Dominik Czernia, PhD, is a physicist at the Institute of Nuclear Physics in Kraków, specializing in condensed matter physics with a focus on molecular magnetism. He has led several national research projects, pioneering innovative approaches to novel materials for high technology. Passionate about making science accessible, Dominik has created various calculators, mostly in physics and math categories. In his free time, he enjoys family walks, city explorations, mountain hiking, and traveling everywhere by bike. See full profile

Check our editorial policy

e Jack Bowater

Eccoti nel calcolatore per la circonferenza goniometrica ⭕. Il nostro strumento ti aiuterà a determinare le coordinate di qualsiasi punto della circonferenza goniometrica, talvolta chiamata circonferenza trigonometrica, circonferenza unitaria o cerchio unitario. Basta inserire l'angolo ∡, e ti mostreremo il seno e il coseno dell'angolo.

Se non sai ancora che cos'è una circonferenza goniometrica, continua a leggere per trovare la risposta. Troverai anche il grafico della circonferenza goniometrica e una spiegazione su come trovare la tangente, il seno e il coseno della circonferenza goniometrica; quindi non aspettare oltre e continua a leggere questo fondamentale calcolatore di trigonometria!

Che cos'è la circonferenza goniometrica?

La circonferenza goniometrica è un cerchio con raggio $1$ (raggio unitario). Nella maggior parte dei casi, è centrato nel punto $(0,0)$ , l'origine del sistema di coordinate.

La circonferenza goniometrica è un concetto molto utile per imparare la trigonometria e la conversione degli angoli.

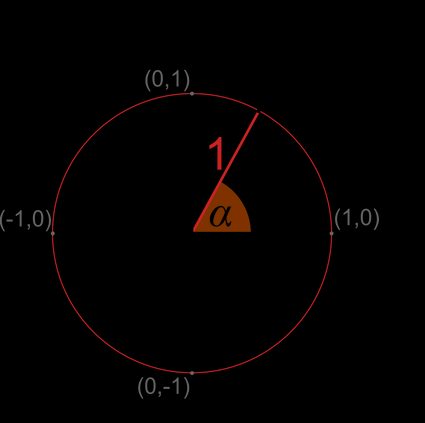
Circonferenza goniometrica in un sistema di coordinate.

Ora che sai cos'è la circonferenza goniometrica, passiamo alle relazioni nella circonferenza goniometrica.

Circonferenza goniometrica: Seno e coseno

Ok, allora perché la circonferenza goniometrica è così utile nella trigonometria?

Prima di tutto, se è anche chiamata circonferenza trigonometrica, ci sarà pure una ragione! Ma passiamo al sodo:

In sintesi

Le relazioni di seno e coseno della circonferenza goniometrica sono le seguenti:

Il seno è la coordinata y; e
Il coseno è la coordinata x.

🙋 Hai bisogno di un'introduzione al seno e al coseno? Visita il nostro calcolatore del seno 🇺🇸 e il calcolatore del coseno 🇺🇸!

Spiegazione dettagliata

Prendiamo un punto A qualsiasi sulla circonferenza goniometrica.

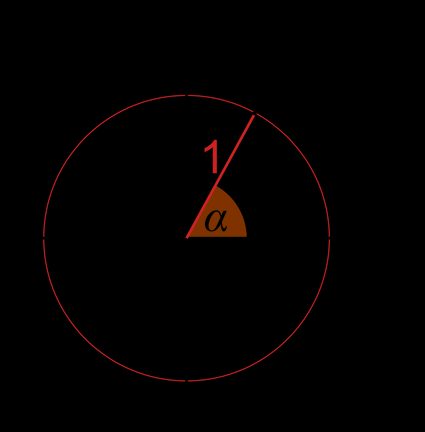
Circonferenza goniometrica in un sistema di coordinate, con punto A(x,y).

Le coordinate di questo punto sono $x$ e $y$ . Trattandosi di una circonferenza goniometrica, il raggio $r$ è uguale a $1$ (distanza tra un punto $P$ e il centro del cerchio):

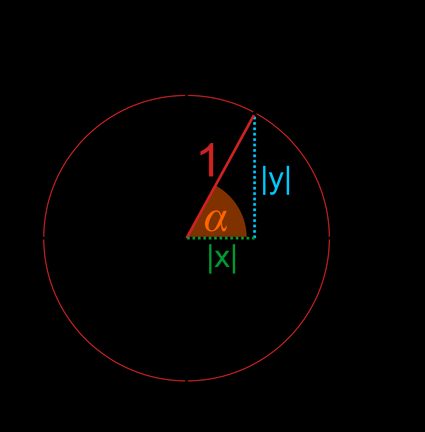
Circonferenza goniometrica in un sistema di coordinate con punto A(x,y) e cateti |x| e |y|

Proiettando il raggio sugli assi $x$ e $y$ , otterremo un triangolo rettangolo, dove $|x|$ e $|y|$ sono le lunghezze dei cateti, e l'ipotenusa è uguale a $1$ :

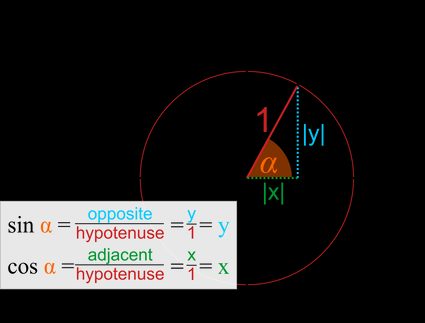
Circonferenza goniometrica in un sistema di coordinate con formule di seno e coseno.

Come in ogni triangolo rettangolo, puoi determinare i valori delle funzioni trigonometriche trovando i rapporti tra i lati:

\sin(\alpha)=\frac{\mathrm{cateto\ opposto}}{\mathrm{ipotenusa}} = \frac{y}{1} = y

Quindi, in altre parole, il seno è la coordinata $y$

\cos(\alpha) = \frac{\mathrm{cateto\ adiacente}}{\mathrm{ipotenusa}} = \frac{x}{1} = x

E il coseno è la coordinata $x$ .

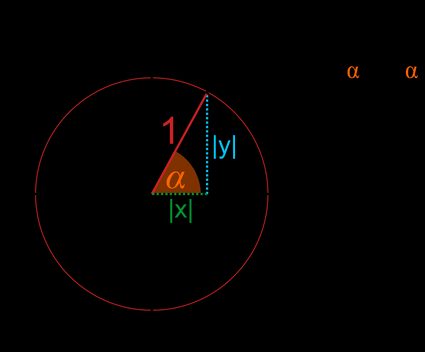
Circonferenza goniometrica in un sistema di coordinate con punto A(x,y) = (cos a, sin a)

L'equazione della circonferenza trigonometrica, derivata direttamente dal teorema di Pitagora, è la seguente:

x^2+y^2=1

Oppure, in modo analogico:

\sin^2(\alpha) + \cos^2(\alpha) = 1

🙋 Per un'analisi approfondita, abbiamo creato il calcolatore della tangente 🇺🇸!

L'intima connessione tra trigonometria e triangoli non può essere più sorprendente! Per saperne di più su questi importanti concetti, visita il calcolatore per il triangolo rettangolo di Omni.

Tangente della circonferenza goniometrica e altre funzioni trigonometriche

Puoi trovare direttamente il valore della tangente della circonferenza goniometrica se ricordi la definizione di tangente:

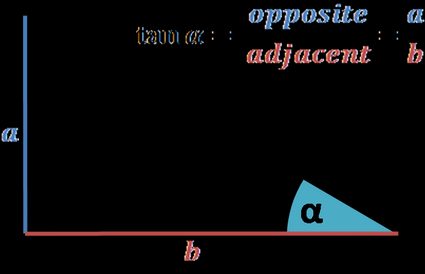
Triangolo rettangolo — Illustrazione della definizione di tangente. Cateto opposto diviso per il cateto adiacente.

Il rapporto tra il cateto opposto e quello adiacente rispetto a un angolo in un triangolo rettangolo.

\tan{\alpha} = \frac{\mathrm{cateto\ opposto}}{\mathrm{cateto\ adiacente}}

Come abbiamo imparato dal paragrafo precedente, $\sin(\alpha) = y$ e $\cos(\alpha) = x$ , quindi:

\tan(\alpha) = \frac{y}{x}

Possiamo anche definire la tangente dell'angolo come il suo seno diviso per il suo coseno:

\tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} = \frac{y}{x}

Il che, ovviamente, ci porterà allo stesso risultato.

Un altro metodo è quello di utilizzare il nostro calcolatore per la circonferenza goniometrica, ovviamente. 😁

Hai ancora fame di sapere e vuoi vedere il valore della tangente sulla circonferenza goniometrica?

È un po' più complicato che determinare il seno e il coseno, che sono semplicemente delle coordinate. Esistono due modi per visualizzare la tangente della circonferenza goniometrica:

Metodo 1

Crea una linea tangente al punto $A$ ;
Questa intersecherà l'asse $x$ nel punto $B$ ; e
La lunghezza del segmento $\bar{AB}$ è il valore della tangente.

Metodo 2

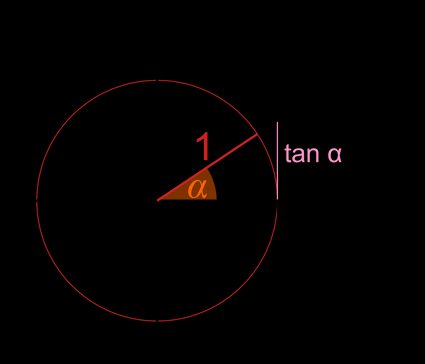
Traccia una linea $x = 1$ ;
Prolunga la linea contenente il raggio;
Nomina l'intersezione di queste due linee come punto $C$ ; e
La tangente, $\tan(\alpha)$ , è la coordinata $y$ del punto $C$ .

In entrambi i metodi, abbiamo creato dei triangoli rettangoli con il lato adiacente pari a 1. 😎

Seno, coseno e tangente non sono le uniche funzioni che puoi costruire sulla circonferenza goniometrica. Oltre alla cotangente, puoi presentare anche altre funzioni meno conosciute, come la secante, la cosecante e il senoverso, la quale non è più utilizzata:

Funzioni trigonometriche basate sul cerchio. — Grafico di Steven G. Johnson, Wikipedia, CC BY-SA.

Grafico della circonferenza goniometrica — Circonferenza goniometrica in radianti e gradi

Il concetto di circonferenza goniometrica, conosciuta anche come circonferenza unitaria, è molto importante perché puoi usarlo per trovare il seno e il coseno di qualsiasi angolo. Di seguito ti presentiamo alcuni angoli comunemente incontrati nel grafico della circonferenza goniometrica:

Ad esempio, come determinare $\sin(150\degree)$ ?

Cerca l'angolo $150\degree$ ; e
Come abbiamo imparato in precedenza, il seno è la coordinata $y$ , quindi prendiamo la seconda coordinata dal punto corrispondente della circonferenza goniometrica:

\qquad \sin(150\degree) = \frac{1}{2}

In alternativa, inserisci l'angolo di 150° nel nostro calcolatore per la circonferenza goniometrica. Ti mostreremo il valore di $\sin(150\degree)$ , ovvero la coordinata $y$ , il coseno, la tangente, e il grafico della circonferenza trigonometrica.

Come memorizzare la circonferenza goniometrica?

Beh, dipende da cosa vuoi memorizzare. 🙃 Ci sono due cose da ricordare quando si parla di circonferenza goniometrica, o circonferenza triconometrica:

Conversione degli angoli, ovvero come passare da un angolo in gradi a uno in termini di $\pi$ (radianti); e
Le funzioni trigonometriche degli angoli più diffusi.

Iniziamo con la prima parte, più semplice. Gli angoli più importanti sono quelli che userai sempre:

$30\degree = \pi/6$ ;
$45\degree = \pi/4$ ;
$60\degree = \pi/3$ ;
$90\degree = \pi/2$ ; e
$360\degree = 2\pi$ — l'angolo giro.

Poiché questi angoli sono molto comuni, cerca di impararli a memoria. ❤️ Per qualsiasi altro angolo, puoi utilizzare la formula di conversione degli angoli:

\alpha\ [\mathrm{rad}] = \frac{\pi}{180\degree}\times \alpha\ [\mathrm{gra}]

La conversione dei radianti della circonferenza goniometrica in gradi non dovrebbe più essere un problema! 💪

L'altra parte — ricordare l'intero grafico della circonferenza goniometrica, con i valori di seno e coseno — è un processo un po' più lungo. Non lo descriveremo qui, ma ti invitiamo a dare un'occhiata a quest'articolo sulla circonferenza goniometrica, o a questa pagina WikiHow. Se preferisci guardare un video 🖥️ piuttosto che leggere 📘, guarda uno di questi due video che spiegano come memorizzare la circonferenza goniometrica:

Circonferenza goniometrica;
Un trucco per ricordare i valori sulla circonferenza goniometrica [EN]; e
Come memorizzare la circonferenza goniometrica in pochi minuti!!! [EN].

Ricorda che puoi sempre attivare la funzione di auto-traduzione su YouTube per comprendere i video.

Inoltre, questa tabella con gli angoli più comuni potrebbe esserti utile:

$\mathrm{\boldsymbol{\alpha}}$ (angolo)		Funzioni trigonometriche
$\mathrm{gra}$	$\mathrm{rad}$	$\sin(\alpha)$	$\cos(\alpha)$	$\tan(\alpha)$
$30\degree$	$\pi/6$	$1/2$	$\sqrt{3}/2$	$\sqrt{3}/3$
$45\degree$	$\pi/4$	$\sqrt{2}/2$	$\sqrt{2}/2$	$1$
$60\degree$	$\pi/3$	$\sqrt{3}/2$	$1/2$	$\sqrt{3}$

E se qualche metodo fallisce, puoi tranquillamente usare il nostro calcolatore per la circonferenza goniometrica — è qui per te, per sempre. ❤️ Speriamo che giocare con questo strumento ti aiuti a capire e a memorizzare i valori della circonferenza trigonometrica!

FAQ

Qual è la tangente di 30 gradi sulla circonferenza goniometrica?

tan 30° = 1/√3. Per trovare questa risposta sulla circonferenza goniometrica, o circonferenza trigonometrica, iniziamo trovando i valori di sin e cos come coordinate y e x, rispettivamente: sin 30° = 1/2 e cos 30° = √3/2. Ora usa la formula. Ricorda che tan 30° = sin 30° / cos 30° = (1/2) / (√3/2) = 1/√3, come indicato. Vedi come è facile?

Come si trova la cosecante sulla circonferenza goniometrica?

Per determinare la cosecante di θ sulla circonferenza goniometrica, o circonferenza trigonometrica:

Dal centro del cerchio disegna il raggio corrispondente all'angolo θ;
Disegna le linee tangenti al cerchio nei punti (0,1) e (0,-1);
Prolunga il raggio del punto 1 in modo che intersechi una di queste tangenti;
La distanza dal centro al punto di intersezione del passo 3 è la cosecante dell'angolo θ; e
Se non c'è un punto di intersezione, la cosecante di θ è indefinita (questo accade quando sin θ = 0).

Come si trova l'arcoseno di 1/2 sulla circonferenza goniometrica?

Poiché l'arcoseno è la funzione inversa della funzione seno, trovare arcsin(1/2) equivale a trovare un angolo il cui seno è uguale a 1/2. Sulla circonferenza goniometrica, chiamata anche circonferenza trigonometrica, i valori del seno sono le coordinate y dei punti sul cerchio. Osservando la circonferenza goniometrica, vediamo che la coordinata y è uguale a 1/2 per l'angolo π/6, cioè 30°.