Trigonometrie Rechner

Dieser Trigonometrie-Rechner hilft dir in zwei gängigen Fällen, in denen Trigonometrie benötigt wird. Verwende den ersten Teil des Rechners, wenn du die Werte von Sinus, Kosinus, Tangens und deren Kehrwertfunktionen finden möchtest. Suchst du die fehlende Seite oder den fehlenden Winkel in einem rechtwinkligen Dreieck mithilfe der Trigonometrie? Unser Tool ist auch hier eine sichere Sache! Gib 2-3 vorgegebene Werte in den zweiten Teil des Rechners ein und du wirst die Antwort im Handumdrehen finden. Scrolle nach unten, wenn du mehr über Trigonometrie erfahren möchtest und wie du sie anwenden kannst.

Omni Calculator hat noch viele andere nützliche Rechner, wenn es um trigonometrische Probleme geht. Schau dir mit dem Sinussatz Rechner und unserem Kosinussatz Rechner zwei bekannte trigonometrische Gesetze an, die dir bei der Lösung von Dreiecken aller Art helfen.

Dieser Trigonometrie-Rechner hat zwei Abschnitte, die zwei verschiedene Funktionen der Trigonometrie ausführen. Die folgende Anleitung soll dir helfen, dich mit diesem Rechner zurechtzufinden:

1. Im ersten Bereich kannst du einen Winkel eingeben und erhältst eine Liste mit trigonometrischen Funktionswerten für diesen Winkel. Um eine andere Einheit einzugeben, klicke auf die Einheit, und gib dann den Winkel ein.

Um zum Beispiel den Wert von sin(45°) zu ermitteln, geben wir einfach 45° als Winkel ein. Der Taschenrechner sagt dir sofort, dass sin(45°) = 0,70710678 ist. Er gibt auch die Werte anderer trigonometrischer Funktionen an, wie cos(45°) und tan(45°).

2. Im zweiten Teil wird die Trigonometrie verwendet, um die fehlenden Parameter eines rechtwinkligen Dreiecks zu bestimmen:

   1. Wähle zunächst aus, welche Parameter des Dreiecks bekannt sind. Du kannst zwischen „zwei Seiten“, „ein Winkel und eine Seite“ und „Flächeninhalt und eine Seite“ wählen.

   2. Sieh dir das Diagramm am Ende des Rechners an, um die Beschriftung der Parameter zu verstehen. Gib die Parameter entsprechend deiner Wahl ein. Wenn du einen Parameter in einer anderen Einheit eingeben musst, ändere die Einheit, bevor du einen Wert eingibst.

   3. Das Tool berechnet die fehlenden Parameter mithilfe der Trigonometrie.

Wir können zum Beispiel die zwei bekannten Seiten a = 7 cm und b = 12 cm in den Rechner eingeben. Wir sehen sofort, dass c = 13,892 cm, α = 30,256° und β = 59,74°.

Wir können diesen Abschnitt auch umgekehrt verwenden! Angenommen, wir kennen den Winkel β = 30°, b = 10 cm und c = 20 cm. Gib zuerst β = 30° ein, und sofort erfahren wir, dass α = 60° ist. Gib nun b = 10 cm ein. Ähnlich verhält es sich mit c = 20 cm, und wir sehen, dass a = 17,32 cm ist.

Wenn du dich fragst, wie die Trigonometrie dir helfen kann, so viel über Dreiecke zu lernen, lies diesen Artikel weiter. Er beantwortet viele wichtige Fragen rund um die Trigonometrie.

Die Trigonometrie ist ein Teilgebiet der Mathematik. Das Wort selbst setzt sich aus den griechischen Worten trigōnon (was „Dreieck” bedeutet) und metron („Maß”) zusammen. Wie der Name vermuten lässt, beschäftigt sich die Trigonometrie vor allem mit Winkeln und Dreiecken; insbesondere definiert und verwendet sie die Beziehungen und Verhältnisse zwischen Winkeln und Seiten in Dreiecken. Die Hauptanwendung ist also das Lösen von Dreiecken, seien es rechtwinklige Dreiecke oder jeder anderen Art von Dreieck, die dir gefällt.

Die Trigonometrie hat viele Anwendungen: von Alltagsproblemen wie der Berechnung der Höhe oder der Entfernung zwischen Objekten bis hin zu Satellitennavigationssystemen, der Astronomie und der Geografie. Außerdem sind Sinus- und Kosinusfunktionen grundlegend für die Beschreibung periodischer Phänomene — dank ihnen können wir oszillierende Bewegungen (wie in unserem Mathematisches Pendel Rechner) und Wellen wie Schall, Vibration oder Licht beschreiben.

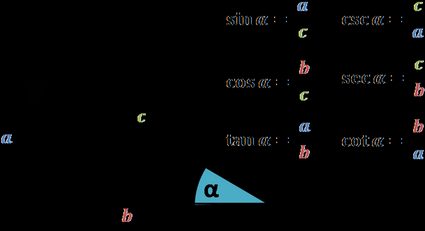
Viele Bereiche der Naturwissenschaften und Ingenieurwissenschaften verwenden Trigonometrie und trigonometrische Funktionen, nämlich: Musik, Akustik, Elektronik, Medizin und medizinische Bildgebung, Biologie, Chemie, Meteorologie, Elektrotechnik, Maschinenbau, Bauingenieurwesen und sogar Wirtschaft. Die trigonometrischen Funktionen sind wirklich überall um uns herum!

Um die fehlenden Seiten oder Winkel des rechtwinkligen Dreiecks zu finden, musst du nur die bekannten Variablen in den Trigonometrie-Rechner eingeben. Du brauchst nur zwei vorgegebene Werte in bestimmten Fällen:

• eine Seite und ein Winkel,
• zwei Seiten oder
• die Fläche und einer Seite.

Denke daran, dass es nicht ausreicht, wenn du nur zwei Winkel kennst, um die Seiten des Dreiecks zu bestimmen. Zwei Dreiecke, die die gleiche Form haben (d. h. gleiche Winkel), können unterschiedlich groß sein (unterschiedliche Seitenlängen haben) — diese Art von Beziehung wird als Ähnlichkeit von Dreiecken bezeichnet. Wenn die Seiten die gleiche Länge haben, sind die Dreiecke kongruent.

*Hi, ich bin Hanna, der Kopf hinter diesem Trigonometrie-Rechnerund promovierte Maschinenbauerin und Expertin in der Entwicklung wissenschaftlicher Werkzeuge. Ich wusste, dass mir ein qualitativ hochwertiger Trigonometrie-Rechner dabei helfen wird, die optimale Schärfentiefe für meine Fotos zu ermitteln, also nahm ich mir die Zeit, um ihn zu entwickeln. Dank ihm habe ich einige super-scharfe Fotos von farbenfrohen Vögeln in freier Wildbahn aufgenommen!

Wir legen besonderen Wert auf die Qualität unserer Inhalte, damit sie so genau und zuverlässig wie möglich sind. Jedes Tool wird von einem geschulten Experten getestet und anschließend von einem Muttersprachler Korrektur gelesen. Mehr über unsere Standards erfährst du in unseren Redaktionsrichtlinien.

Trigonometrie ist die Lehre von den Verhältnissen innerhalb eines Dreiecks. Bei rechtwinkligen Dreiecken ist das Verhältnis zwischen zwei beliebigen Seiten immer gleich und wird durch die trigonometrischen Verhältnisse cos, sin und tan angegeben. Die Trigonometrie kann auch dabei helfen, fehlende Informationen über Dreiecke zu finden, z. B. mit dem Sinussatz.

1. Finde heraus, welche zwei dieser Parameter du gegeben hast: die Hypotenuse, Ankathete, Gegenkathete oder den Winkel.
2. Finde heraus, welche der verbleibenden Optionen du berechnen möchtest.
3. Wähle die Beziehung aus, die du brauchst.
4. Setze die Daten, die du hast, in die Gleichung ein.
5. Stelle die Gleichung nach der Unbekannten um und löse sie.
6. Überprüfe deine Antworten mit unserem Trigonometrie-Rechner.

Trigonometrie kann am Anfang etwas schwer zu verstehen sein, aber nach etwas Übung wirst du sie meistern! Hier sind einige Tipps zur Trigonometrie:

• Beschrifte die Hypotenuse, die Ankathete und die Gegenkathete deines Dreiecks, damit du herausfinden kannst, welche Identität du verwenden musst.

Merke dir:

• Tangens = Gegenkathete durch Ankathete,
• Sinus = Gegenkathete durch Hypotenuse, und
• Kosinus = Ankathete durch Hypotenuse.

Die Trigonometrie wird verwendet, um Informationen über jede Art von Dreiecken zu finden, insbesondere über rechtwinklige Dreiecke. Da Dreiecke in der Natur überall vorkommen, wird die Trigonometrie außerhalb der Mathematik viel in Bereichen wie dem Bauwesen, der Physik, der Chemietechnik und der Astronomie verwendet.

Da es sich bei der Trigonometrie um die Beziehung zwischen Winkeln und Seiten eines Dreiecks handelt, hat sie niemand erfunden, sie war auch dann schon da, als noch niemand von ihr wusste! Die ersten Menschen, die einen Teil der Trigonometrie entdeckten, waren die alten Ägypter und Babylonier, aber die Griechen Euklid und Archimedes bewiesen die Identitäten zuerst, obwohl sie es mithilfe von Formen und nicht mit Algebra taten.

Trigonometrie wird normalerweise Teenagern im Alter von 13-15 Jahren beigebracht. Das entspricht der Oberstufenklasse 9 in Deutschland. Das genaue Alter, in dem Trigonometrie unterrichtet wird, hängt aber vom Land, der Schule und dem Lerntempo der Schüler ab.

1. Finde heraus, welche trigonometrische Beziehung du verwendest.
2. Nimm die umgekehrte Identität deiner Dezimalzahl, z. B. sin⁻¹(0,5).
3. Die resultierende Zahl ist der Grad deines Winkels.
4. Prüfe deine Ergebnisse mit unserem Trigonometrie-Rechner.

1. Zeichne dein Dreieck und markiere die Höhe. Du wirst das Dreieck in zwei kleinere Dreiecke aufteilen müssen.
2. Löse eines der kleinen Dreiecke mithilfe der normalen Trigonometrie auf, um die Höhe zu bestimmen. Die gegenüberliegende oder benachbarte Seite ist nun die Hypotenuse des kleineren Dreiecks.
3. Prüfe deine Antworten mit Omni Calculator.