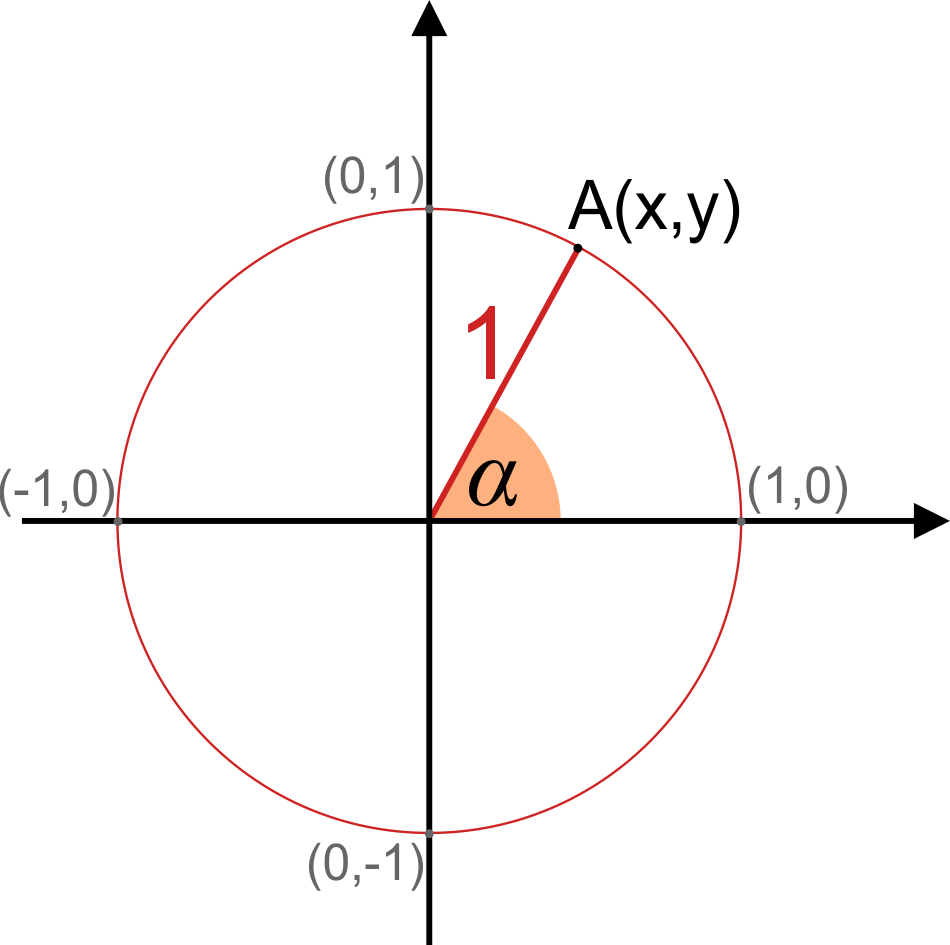
Kalkulator okręgu jednostkowego

Witamy w kalkulatorze okręgu jednostkowego ⭕. Nasze narzędzie pomoże ci określić współrzędne dowolnego punktu na okręgu jednostkowym. Po prostu wprowadź kąt ∡, a my obliczymy sinus i cosinus kąta.

Jeśli nie wiesz czym jest okrąg jednostkowy, przewiń w dół, a znajdziesz odpowiedź. Wykres okręgu jednostkowego oraz wyjaśnienie jak znaleźć styczną do okręgu jednostkowego, sinus i cosinus są zawarte w poniższym artykule, więc nie czekaj dłużej — czytaj dalej, aby poznać tajniki trygonometrii!

Okrąg jednostkowy to okrąg o promieniu 1 (promień jednostkowy). W większości przypadków jego środek znajduje się w punkcie $(0,0)$, będącym początkiem układu współrzędnych.

Okrąg jednostkowy jest bardzo przydatnym pojęciem podczas nauki trygonometrii i konwersji kątów.

Teraz gdy już wiesz, czym jest okrąg jednostkowy, przejdźmy do relacji matematycznych w okręgu o promieniu jednostkowym.

OK, więc dlaczego okrąg jednostkowy jest tak przydatny w trygonometrii?

W skrócie:

Relacje okręgu jednostkowego dla sinusa i cosinusa:

• Sinus jest współrzędną y.
• Cosinus jest współrzędną x.

Standardowe wyjaśnienie:

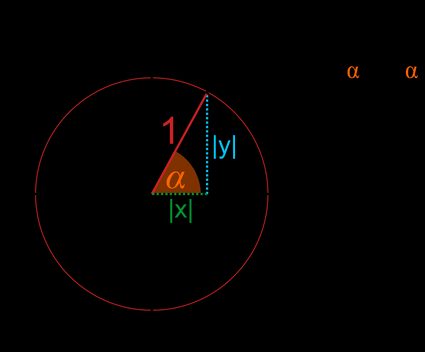
Weźmy dowolny punkt A na obwodzie okręgu jednostkowego.

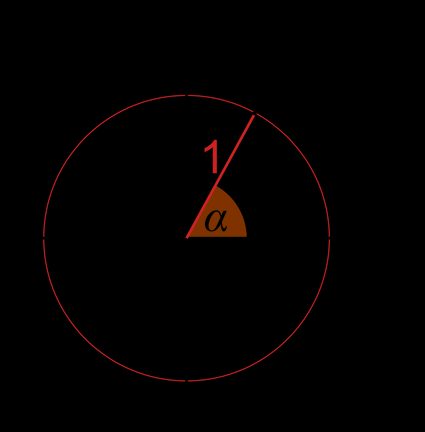
• Współrzędne tego punktu to $x$ i $y$. Ponieważ jest to okrąg jednostkowy, promień r jest równy $1$ (odległość między punktem $P$ a środkiem okręgu).

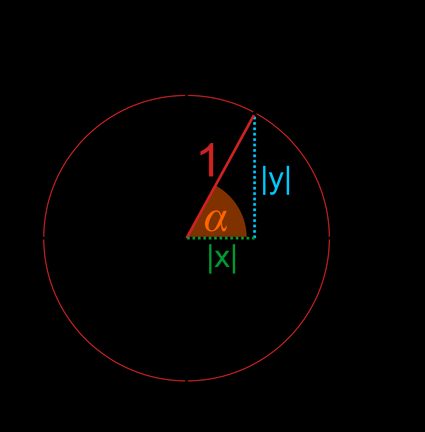
• Rzutując promień na osie x i y, otrzymamy trójkąt prostokątny, w którym $|x|$ i $|y|$ są długościami przyprostokątnych, a przeciwprostokątna jest równa $1$.

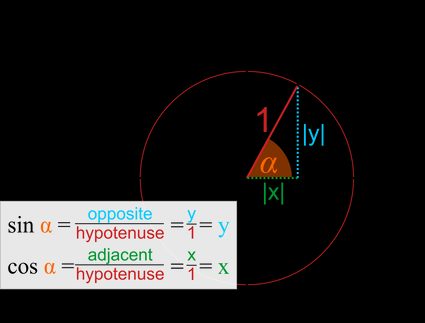
• Jak w każdym trójkącie prostokątnym, możesz określić wartości funkcji trygonometrycznych, znajdując stosunki boków:

Innymi słowy, sinus jest współrzędną y:

A cosinus to współrzędna x.

Równanie okręgu jednostkowego, wynikające bezpośrednio z twierdzenia Pitagorasa, wygląda następująco:

Lub analogicznie:

Ten ścisły związek między trygonometrią a trójkątami nie może być bardziej zaskakujący! Dowiedz się więcej o tych ważnych pojęciach w Omni kalkulatorze trójkąta prostokątnego.

Możesz znaleźć wartość stycznej okręgu jednostkowego bezpośrednio, jeśli pamiętasz definicję stycznej:

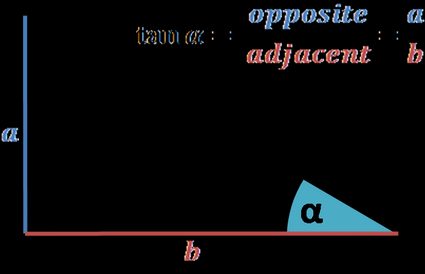
Stosunek przeciwległych i przyległych boków do kąta w trójkącie prostokątnym.

Jak dowiedzieliśmy się z poprzedniego akapitu, $\sin(\alpha) = y$ i $\cos(\alpha) = x$, więc:

Możemy również zdefiniować tangens kąta jako jego sinus podzielony przez jego cosinus:

Co oczywiście da nam ten sam rezultat.

Inną metodą jest oczywiście użycie naszego kalkulatora okręgu jednostkowego. 😁

Ale co, jeśli nie zadowala cię tylko ta wartość i chcesz faktycznie zobaczyć tę wartość stycznej na okręgu jednostkowym?

Jest to nieco bardziej skomplikowane niż określenie sinusa i cosinusa — które są po prostu współrzędnymi. Istnieją dwa sposoby wyświetlenia stycznej na okręgu jednostkowym:

Metoda 1:

1. Utwórz linię styczną w punkcie $A$.
2. Przetnie ona oś x w punkcie $B$.
3. Długość odcinka $\bar{AB}$ jest wartością stycznej

Metoda 2:

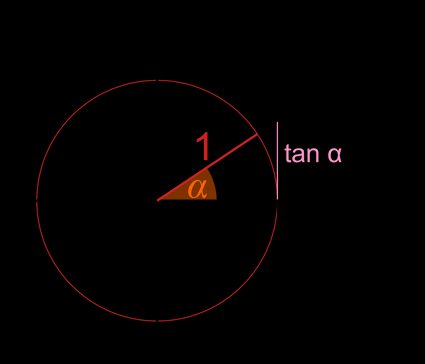
1. Narysuj linię $x = 1$.
2. Przedłuż linię zawierającą promień.
3. Nazwij punkt przecięcia tych dwóch linii jako punkt $C$.
4. Styczna, $\tg(\alpha)$, jest współrzędną y punktu $C$.

W obu metodach utworzyliśmy trójkąty prostokątne z przyległym bokiem równym 1 😎

Sinus, cosinus i tangens nie są jedynymi funkcjami, które możesz skonstruować na okręgu jednostkowym. Oprócz stycznej — cotangensa — możesz również przedstawić inne mniej znane funkcje, np. sekans, kosekans i nieużywana już funkcja 1-cos alfa:

Koncepcja okręgu jednostkowego jest bardzo ważna, ponieważ możesz jej użyć do znalezienia sinusa i cosinusa dowolnego kąta. Poniżej przedstawiamy kilka często spotykanych kątów na wykresie okręgu jednostkowego:

Jako przykład — jak określić $\sin(150\degree)$?

1. Wyszukaj kąt $150\degree$.
2. Jak dowiedzieliśmy się wcześniej — sinus jest współrzędną y, więc bierzemy drugą współrzędną z odpowiedniego punktu na okręgu jednostkowym:

Alternatywnie, wprowadź kąt 150° do naszego kalkulatora okręgu jednostkowego. Pokażemy ci wartość $\sin(150\degree)$ współrzędnej y, a także cosinus, tangens i wykres okręgu jednostkowego.

Cóż, to zależy od tego, co chcesz zapamiętać 🙃. Istnieją dwie najważniejsze rzeczy do zapamiętania, jeśli chodzi o okrąg jednostkowy:

1. Konwersja kątów, czyli jak zamienić kąt w stopniach na kąt w $\pi$ (radianach okręgu jednostkowego);

2. Funkcje trygonometryczne popularnych kątów.

Zacznijmy od łatwiejszej pierwszej części. Najważniejsze kąty to te, których będziesz używać przez cały czas:

• $30\degree = \pi/6$
• $45\degree = \pi/4$
• $60\degree = \pi/3$
• $90\degree = \pi/2$
• Kąt pełny, $360\degree = 2\pi$

Ponieważ kąty te są bardzo powszechne, spróbuj nauczyć się ich na pamięć ❤️. Dla każdego innego kąta możesz użyć formuły konwersji kąta:

Konwersja radianów okręgu jednostkowego na stopnie nie powinna już stanowić problemu! 💪

Druga część — zapamiętanie całego wykresu okręgu jednostkowego z wartościami sinusów i cosinusów — jest nieco dłuższym procesem. Nie będziemy go tutaj opisywać, ale zachęcamy do zapoznania się z nimi w wolnym czasie. Jeśli bardziej lubisz oglądać filmy 🖥️ niż czytać 📘, obejrzyj jeden z tych dwóch filmów wyjaśniających, jak zapamiętać okrąg jednostkowy:

• A Trick to Remember Values on The Unit Circle,
• Jak zapamiętać okrąg jednostkowy w kilka minut!!!.

Przydatna może być również tabela z często używanymi kątami:

A jeśli któraś z metod zawiedzie, możesz skorzystać z naszego kalkulatora okręgu jednostkowego — jest do twojej dyspozycji na zawsze ❤️. Mamy nadzieję, że zabawa z tym narzędziem pomoże ci zrozumieć i zapamiętać wartości okręgu jednostkowego!

tg 30° = 1/√3. Aby znaleźć tę odpowiedź na okręgu jednostkowym, zacznijmy od znalezienia wartości sin i cos odpowiednio jako współrzędnej y i współrzędnej x: sin 30° = 1/2 i cos 30° = √3/2. Teraz użyj wzoru. Przypomnij sobie, że tan 30° = sin 30° / cos 30° = (1/2) / (√3/2) = 1/√3, zgodnie z twierdzeniem. Widzisz, jakie to proste?

Wyznacz kosekans funkcji θ na okręgu jednostkowym:

1. Ze środka okręgu narysuj promień odpowiadający kątowi θ.
2. Narysuj linie styczne do okręgu w punktach (0,1) i (0,-1).
3. Wydłuż promień z kroku 1 tak, aby przecinał jedną z tych stycznych.
4. Odległość od środka do punktu przecięcia z kroku 3 to kosekans twojego kąta θ.
5. Jeśli nie ma punktu przecięcia, kosekans kąta θ jest niezdefiniowany (dzieje się tak, gdy sin θ = 0).

Ponieważ arcsin (arcus sinus) jest odwrotnością funkcji sinus, znalezienie arcsin(1/2) jest równoważne znalezieniu kąta, którego sinus jest równy 1/2. Na okręgu jednostkowym wartości sinusa są współrzędnymi y punktów na okręgu. Patrząc na okrąg jednostkowy, widzimy, że współrzędna y jest równa 1/2 dla kąta π/6``, czyli 30°`.