Calculadora de triángulos isóceles

La calculadora de triángulos isósceles es la mejor opción si buscas una solución rápida a tus problemas de geometría. Averigua el área del triángulo isósceles, su perímetro, radio de la circunferencia inscrita, circunradio, alturas y ángulos, todo en un solo lugar. Si quieres construir una perrera, averiguar el área del frontón isósceles de un templo griego, o simplemente hacer tus deberes de matemáticas, esta herramienta está aquí para ti. Experimenta con la calculadora o sigue leyendo para saber más sobre las fórmulas del triángulo isósceles y el teorema del triángulo isósceles.

Un triángulo isósceles es un triángulo con dos lados de igual longitud, llamados catetos. El tercer lado del triángulo se llama base. El ángulo del vértice es el ángulo entre los catetos. Los ángulos que tienen la base como uno de sus lados se llaman ángulos de la base.

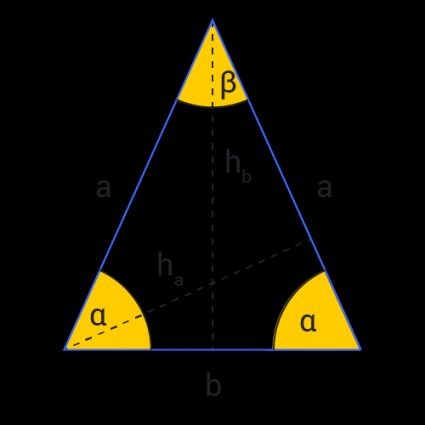
He aquí las propiedades más importantes de los triángulos isósceles:

• Tiene un eje de simetría a lo largo de la altura de su vértice;
• Los dos ángulos adyacentes a la base son iguales;
• El triángulo isósceles puede ser agudo, recto u obtuso, pero solo depende del ángulo del vértice (los ángulos adyacentes a la base son siempre agudos)

El triángulo equilátero es un caso especial de triángulo isósceles. Puedes conocer todos los tipos posibles de triángulos en la calculadora de clasificación de triángulos 🇺🇸. Además, si quieres profundizar en las características de un triángulo equilátero, consulta calculadora de triángulos equiláteros

Para calcular el área de un triángulo isósceles, puedes utilizar muchas fórmulas diferentes. Las más populares son las ecuaciones:

1. Dado el cateto a y la base b:

   área = (1/4) × b × √( 4 × a² - b² )

2. Dada la altura h desde el vértice y la base b o la altura h2 desde los otros dos vértices y el cateto a:

   área = (1/2) × h × b = 1/2 × h2 × a

3. Dado cualquier ángulo y cateto o base

   área = (1/2) × a × b × sen(ángulo_base) = (1/2) × a² × sen(ángulo_vértice)

También puedes consultar nuestra calculadora del área de un triángulo para encontrar otras ecuaciones, que sirven para todos los tipos de triángulo, no solo para el isósceles.

Para calcular el perímetro del triángulo isósceles, basta con sumar todos los lados del triángulo:
perímetro = a + a + b = 2 × a + b

El teorema del triángulo isósceles, también conocido como teorema de los ángulos de la base, afirma que si dos lados de un triángulo son congruentes, los ángulos opuestos a dichos lados son congruentes.

También existe el teorema inverso, que afirma que si dos ángulos de un triángulo son congruentes, los lados opuestos a dichos ángulos son congruentes.

Un triángulo áureo, también llamado triángulo sublime o triángulo de oro, es un triángulo isósceles en el que el cateto está en la proporción áurea con respecto a la base:

a / b = φ ~ 1.618

El triángulo áureo tiene algunas propiedades inusuales:

• Es el único triángulo con tres ángulos en proporción 2:2:1
• Es la forma de los triángulos que se encuentran en las puntas de los pentagramas
• Sirve para formar una espiral logarítmica

Veamos cómo utilizar esta herramienta con un sencillo ejemplo. Echa un vistazo a esta solución paso a paso:

1. Determina cuál es tu primer valor dado. Supongamos que queremos comprobar las propiedades del triángulo áureo. Escribe 1.681 cm en la casilla “Cateto”.
2. Introduce el segundo parámetro conocido. Por ejemplo, toma una base igual 1 cm.
3. ¡Todos los demás parámetros se calculan en un abrir y cerrar de ojos! Comprobamos, por ejemplo, que el perímetro del triángulo isósceles es de 4.362 cm y que los ángulos del triángulo áureo son iguales a 72.2° y 34.6°: la proporción es igual a 2:2:1, efectivamente.

Puedes utilizar esta calculadora para determinar parámetros distintos de los del ejemplo, pero recuerda que, en general, hay dos triángulos isósceles distintos para un área dada y otros parámetros, por ejemplo, la longitud de los catetos. Nuestra calculadora te mostrará una posible solución.