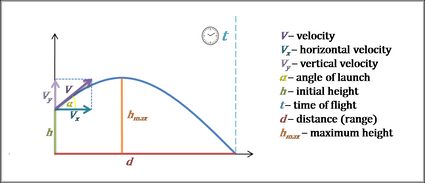
Calcolatore del Moto Parabolico

Il nostro calcolatore del moto parabolico è uno strumento che ti aiuterà ad analizzare il moto parabolico del proiettile. Può trovare il tempo di volo, ma anche le componenti della velocità, la gittata del proiettile e l'altezza massima di volo. Continua a leggere se vuoi capire cos'è il moto parabolico o il moto del proiettile, familiarizzare con la definizione di moto parabolico e determinare i valori sopra citati utilizzando le equazioni del moto parabolico.

Preferisci guardare piuttosto che leggere? Impara tutto quello che ti serve in 90 secondi con questo video che abbiamo creato per te:

Immagina un arciere che lancia una freccia in aria. Inizia a muoversi in alto e in avanti, con una certa inclinazione rispetto al terreno. Più vola, più lenta è la sua ascesa e infine inizia a scendere, muovendosi verso il basso, poi in avanti e infine toccando di nuovo il suolo. Se potessimo tracciare il suo percorso, sarebbe una curva chiamata traiettoria a forma di parabola. Un oggetto che si muove in questo modo è un proiettile. A proposito, abbiamo il calcolatore per la velocità media delle frecce che analizza il movimento delle frecce — provalo!

Su un proiettile agisce una sola forza — la forza di gravità. La resistenza dell'aria viene sempre omessa. Se disegnassi il diagramma del corpo libero di un oggetto del genere, dovresti disegnare solo un vettore verso il basso e indicarlo come "gravità". Se ci fossero altre forze che agiscono sul corpo, allora — per la definizione di moto parabolico — non sarebbe un proiettile.

Il moto parabolico è piuttosto logico. Supponiamo di conoscere la velocità iniziale dell'oggetto $V$, l'angolo di lancio $\alpha$ e l'altezza iniziale $h$. Il nostro calcolatore del moto parabolico segue questi passaggi per trovare tutti i parametri rimanenti:

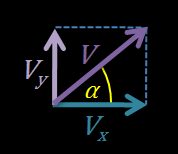
1. Calcola le componenti della velocità.

• La componente orizzontale della velocità $V_\mathrm x$ è uguale a $V \cos\alpha$.

• La componente verticale della velocità $V_\mathrm y$ è uguale a $V \sin\alpha$.

• I tre vettori — $V$, $V_\mathrm x$ e $V_\mathrm y$ — formano un triangolo rettangolo.

Se la componente verticale della velocità è uguale a 0, allora si tratta di un moto orizzontale del proiettile. Se, inoltre, $α = 90°$, allora si tratta di un caso di caduta libera. Abbiamo affrontato entrambi i problemi rispettivamente nel calcolatore del moto proiettile orizzontale 🇺🇸 e nel calcolatore della caduta libera.

2. Scrivi le equazioni del moto.

Distanza:

• La distanza orizzontale percorsa può essere espressa con la formula $x = V_\mathrm x t$ dove $t$ è il tempo.
• La distanza verticale dal suolo è descritta dalla formula $y = h + V_\mathrm{y0} t - g t^2 / 2$, dove $g$ è l'accelerazione di gravità e $V_\mathrm{y0}$ è la velocità verticale iniziale.

Velocità:

• La velocità orizzontale è uguale a $V_\mathrm x$.
• La velocità verticale può essere espressa come $V_\mathrm y = V_\mathrm{y0} - g t$.

Accelerazione:

• L'accelerazione orizzontale è uguale a 0.
• L'accelerazione verticale è uguale a $-g$ (perché solo la gravità agisce sul proiettile).

3. Calcola il tempo di volo.

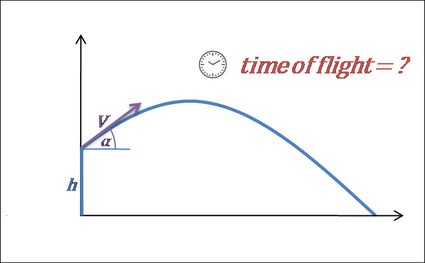
• Il volo termina quando il proiettile colpisce il suolo. Possiamo dire che questo avviene quando la distanza verticale dal suolo è uguale a 0. Nel caso in cui l'altezza iniziale sia 0, la formula può essere scritta come; $V_\mathrm{y0} t - g t^2 / 2 = 0$. Quindi, da questa equazione, scopriamo che il tempo di volo è

• Tuttavia, se stiamo lanciando l'oggetto da una certa altezza, la formula non si riduce così bene come prima e otteniamo un'equazione quadratica da risolvere: $h + V_\mathrm{y0} t - g t^2 / 2 = 0$. Dopo aver risolto questa equazione, otteniamo:

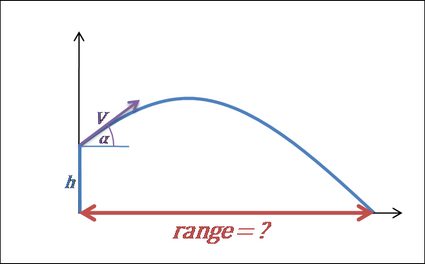
4. Calcola la gittata del proiettile.

• La gittata del proiettile è la distanza orizzontale totale percorsa durante il tempo di volo. Anche in questo caso, se stiamo lanciando l'oggetto da terra (altezza iniziale = 0), possiamo scrivere la formula come $R = V_\mathrm x t = V_\mathrm x \times 2 \times V_\mathrm{y0} / g$. Può anche essere trasformata nella forma; $R = V^2_0 \sin(2\alpha) / g$

• Le cose si complicano per altezze iniziali diverse da 0. Quindi, dobbiamo sostituire la formula lunga del passo precedente come $t$

• Il raggio d'azione è particolarmente importante nella balistica. Ne abbiamo parlato più dettagliatamente nel calcolatore del coefficiente balistico 🇺🇸.

5. Calcola l'altezza massima.

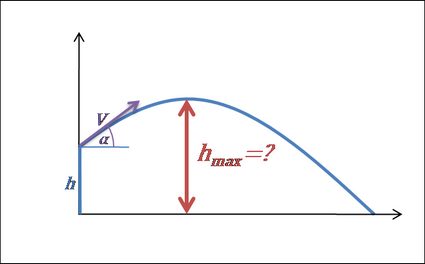
• Quando il proiettile raggiunge l'altezza massima, smette di muoversi verso l'alto e inizia a cadere. Ciò significa che la componente verticale della sua velocità passa da positiva a negativa — in altre parole, è uguale a 0 per un breve momento al tempo $t(V_\mathrm y=0)$.
• Se $V_\mathrm {y0} - g t(V_\mathrm y=0) = 0$, allora possiamo riformulare l'equazione in $t(V_\mathrm y=0) = V_\mathrm{y0} / g$.
• Ora dobbiamo semplicemente trovare la distanza verticale dal suolo in quel momento:

• Fortunatamente, nel caso del lancio di un proiettile da una certa altezza iniziale $h$, dobbiamo semplicemente aggiungere questo valore alla formula finale:

Ci sono stati un sacco di calcoli! Riassumiamo il tutto per ottenere le equazioni fondamentali del moto del proiettile:

1. Lancio dell'oggetto dal suolo (altezza iniziale h = 0):

• Componente orizzontale della velocità — $V_\mathrm x = V_0 \cos \alpha$;
• Componente verticale della velocità — $V_\mathrm y = V_0 \sin \alpha - gt$;
• Tempo di volo — $t = 2 V_\mathrm{y0} / g$;
• Portata del proiettile — $R = 2 V_\mathrm x V_\mathrm{y0} / g$; e
• Altezza massima — $h_\mathrm{max} = V^2_\mathrm{y0} / (2 g)$.

2. Lancio dell'oggetto da una certa altezza (altezza iniziale h > 0):

• Componente della velocità orizzontale — $V_\mathrm x = V_0 \cos \alpha$;
• Componente verticale della velocità — $V_\mathrm y = V _0 \sin \alpha - gt$;
• Tempo di volo — $t = \left[V_\mathrm{y0} + \sqrt{V^2_\mathrm{y0} + 2 g h}\right] / g$;
• Portata del proiettile — $R = V_\mathrm x \left[V_\mathrm{y0} + \sqrt{V^2_\mathrm{y0} + 2 g h}\right] / g$; e
• Altezza massima — $h_\mathrm{max} = h + V^2_ \mathrm{y0} / (2 g)$.

Utilizzare il nostro calcolatore del moto parabolico ti farà sicuramente risparmiare molto tempo. Può anche funzionare "al contrario". Ad esempio, inserisci il tempo di volo, la distanza e l'altezza iniziale e vedrai che il calcolatore farà tutti i calcoli per te!

Assicurati di dare un'occhiata anche al calcolatore per la parabola per saperne di più su questa curva dal punto di vista matematico.