Quadratic Formula Calculator

If you need to solve an equation of the form Ax² + Bx + C = 0, this quadratic formula calculator is here to help you. With just a few clicks, you will be able to solve even the most challenging problems. This article describes in detail what is the quadratic formula and what the symbols A, B, and C stand for. It also explains how to solve quadratic equations, which have a negative discriminant and no real roots.

The quadratic formula is the solution of a second-degree polynomial equation of the following form:

Ax² + Bx + C = 0

If you can rewrite your equation in this form, it means that it can be solved with the quadratic formula. A solution to this equation is also called a root of the equation.

The quadratic formula is as follows:

x = (-B ± √Δ)/2A

where:

• Δ = B² – 4AC

Using this formula, you can find the solutions to any quadratic equation. Note that there are three possible options for obtaining a result:

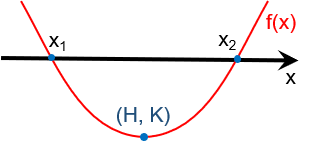
• The quadratic equation has two unique roots when Δ > 0. Then, the first solution of the quadratic formula is x₁ = (-B + √Δ)/2A, and the second is x₂ = (-B – √Δ)/2A.

• The quadratic equation has only one root when Δ = 0. The solution is equal to x = -B/2A. It is sometimes called a repeated or double root.

• The quadratic equation has no real solutions for Δ < 0.

You can also graph the function y = Ax² + Bx + C. It's shape is a parabola, and the roots of the quadratic equation are the x-intercepts of this function.

A, B, and C are the coefficients of the quadratic equation. They are all real numbers, not dependent on x. If A = 0, then the equation is not quadratic, but linear.

If B² < 4AC, then the discriminant Δ will be negative. It means that such an equation has no real roots.

1. Write down your equation. Let's assume it is 4x² + 3x – 7 = -4 – x.

2. Bring the equation to the form Ax² + Bx + C = 0. In this example, we will do it in the following steps:

   4x² + 3x - 7 = -4 – x

   4x² + (3 + 1)x + (-7 + 4) = 0

   4x² + 4x - 3 = 0

3. Calculate the discriminant.

   Δ = B² – 4AC = 4² - 4×4×(-3) = 16 + 48 = 64.

4. Decide whether the discriminant is greater, equal, or lower than 0. In our case, the discriminant is greater than 0, which means that this equation has two unique roots.

5. Calculate the two roots using the quadratic formula.

   x₁ = (-B + √Δ)/2A = (-4 +√64) / (2×4) = (-4 + 8) / 8 = 4/8 = 0.5

   x₂ = (-B – √Δ)/2A= (-4 -√64) / (2×4) = (-4 – 8) / 8 = -12/8 = -1.5

6. The roots of your equation are x₁ = 0.5 and x₂ = -1.5.

You can also simply type the values of A, B, and C into our quadratic equation calculator and let it perform all the calculations for you.

Make sure you have written down the correct number of digits using our significant figures calculator.

Even though the quadratic formula calculator indicates when the equation has no real roots, it is possible to find the solution of a quadratic equation with a negative discriminant. These roots will be complex numbers.

Each complex number is a sum of real and imaginary parts. The imaginary part is always equal to the number i = √(-1) multiplied by a real number.

The quadratic formula remains the same in this case.

x = (-B ± √Δ)/2A

Notice that, as Δ < 0, the square root of the discriminant will be an imaginary value. Hence:

Re(x) = -B/2A

Im(x) = ± (√Δ)/2A

For instance, consider the equation x^2 + 1 = 0. Its discriminant is

Δ = B² – 4AC = 0² - 4×1×1 = -4,

and so the equation admits two distinct complex solutions:

x₁ = (-B + √Δ)/2A = (0 + 2i) / (2×1) = i

x₂ = (-B – √Δ)/2A= (0 - 2i) / (2×1) = -i

Because the discriminant is negative, neither solution is a real number.

Here is one problem that makes use of the quadratic formula. Suppose that we want to split a line segment into two pieces, a longer one of length a and a shorter one of length b so that the ratio a/b of their lengths is the same as (a+b)/a, the ratio of the length of the whole segment to the length of the longer piece. What will the ratio be?

Mathematically, this means that we need to solve the equation a/b = (a+b)/a. This is an equation in two variables a and b, but we're not interested in knowing their individual values, only their ratio. If we denote their ratio as ϕ = a/b, then the equation that we need to solve becomes

ϕ = a/b = (a+b)/a = 1 + b/a = 1 + 1/ϕ

While this task doesn't look easy, we can turn this equation into a quadratic one. Indeed, by multiplying both sides of the equation by ϕ, we get:

ϕ² = ϕ + 1

which is a quadratic equation! Moving ϕ + 1 to the left-hand side, we obtain an equation:

ϕ² - ϕ - 1 = 0

that can be solved using our quadratic formula. Indeed, the discriminant is:

Δ = B² – 4AC = -1 - 4 × 1 × (-1) = 5

and so the equation admits two distinct solutions:

x₁ = (-B + √Δ)/2A = (-1 + √5) / 2 =1.618...

x₂ = (-B – √Δ)/2A= (-1 - √5) / 2 = -0.618...

Notice that one of these solutions is positive while the other is negative. Since we are interested in finding a ratio of two positive numbers (because lengths are always positive), the first solution is the one that we are looking for. So ϕ = 1.618...

The number ϕ = 1.618... is called golden ratio or divide proportion, and it has stunning appearances in various places in mathematics. For example:

• The ratio of two consecutive Fibonacci numbers approaches ϕ; and
• In a regular pentagon, the ratio of the diagonal to the side is ϕ.

The golden ratio has gained fame outside of mathematics. It is often deemed to be the most aesthetically pleasing proportion; hence its second name, the divine proportion. For this reason, it was featured in the 16^th century publication "De Divina Proportione" (On the Divine Proportion) by Luca Pacioli, with illustrations by Leonardo da Vinci. The publication discusses various appearances of the golden ratio in art and architecture.

Many historical and contemporary sources claim that the golden ratio is also ubiquitous in nature. Some examples are:

• Growth pattern of leaves;
• Geometrical surfaces of some vegetables and shells; and
• Proportions of the bones of some animals.

However, while we can't deny the presence of geometrical patterns in nature, we can't confirm the exactness of the proportions of the examples above: some present huge variations, while others only approximate the golden ratio.

An alternative way of dealing with quadratic equations is factoring trinomials. And it really helps if you're able to quickly recognize perfect square trinomials. The next step is to learn how to graph quadratic inequalities.

Do you still want more math after learning all about solving quadratic equations? Omni has over 240 math calculators to explore. In particular, we recommend you take a look at our cubic equation solver. We also recommend you check out the Computer Technology For Math Excellence's webpage. They have a vast collection of resources to learn all about math, with particular attention to the Common Core curriculum.