Kalkulator równania kierunkowego prostej

Omni kalkulator równania kierunkowego prostej nauczy cię jak znaleźć równanie prostej na podstawie dowolnych dwóch punktów, przez które ta prosta przechodzi. Pomożemy ci określić współczynnik kierunkowy i wyraz wolny oraz punkty przecięcia z osiami y i x (tzw. miejsce zerowe). A wszystko to, przy użyciu równania kierunkowego prostej.

W dalszej części tekstu dowiesz się, czym jest równanie liniowe w postaci kierunkowej, jak znaleźć równanie prostej i jakie znaczenie ma ten wzór w życiu codziennym.

Dowolna prosta na płaskiej płaszczyźnie może być opisana matematycznie jako relacja pomiędzy pionowym (oś y) i poziomym (oś x) położeniem każdego z punktów tworzących linię prostą. Relacja ta może być zapisana jako y = [coś z x]. Konkretna forma [coś z x] określi, jaki mamy rodzaj krzywej. Na przykład, y = x² + x jest parabolą, zwaną również funkcją kwadratową. Z drugiej strony, y = ax + b (gdzie a i b reprezentują dowolne liczby rzeczywiste) jest zależnością typową dla linii prostej.

W naszym kalkulatorze równania kierunkowego skupimy się tylko na linii prostej. Możesz sprawdzić również Omni kalkulator średniego tempa zmian, aby znaleźć związek między współrzędnymi dla funkcji nieliniowych.

Równania liniowe lub równania linii prostej można szybko rozpoznać, ponieważ nie zawierają one wyrażeń z potęgami (np. można znaleźć w nich x lub y, ale nigdy x²). Każde równanie liniowe opisuje prostą, która może być wyrażona za pomocą równania kierunkowego.

Jak widzieliśmy wcześniej, równanie dowolnej prostej można zapisać w postaci y = ax + b. Jest to tak zwana postać kierunkowa, ponieważ daje dwie ważne informacje: współczynnik kierunkowy a i wyraz wolny b, czyli punkt przecięcia z osią y. Wartości te można później wykorzystać do interpolacji liniowej.

Termin współczynnik kierunkowy oznacza nachylenie lub gradient prostej. Mówi nam, jak bardzo zmienia się y przy stałej zmianie x. Jeśli jest dodatni, to wartość y wzrasta wraz ze wzrostem x. Jeśli jest ujemny, to y maleje wraz ze wzrostem x. Możesz przeczytać więcej na ten temat w opisie naszego kalkulatora nachylenia prostej.

Wyraz wolny (punkt przecięcia z osią y) to wartość y, przy której prosta przecina oś rzędnych. Aby go znaleźć, należy podstawić x = 0 w równaniu liniowym. Później zobaczysz, dlaczego punkt przecięcia z osią y jest ważnym parametrem w równaniach liniowych, a także dowiesz się o fizycznym znaczeniu jego wartości w niektórych rzeczywistych przykładach.

Nadal chcesz wiedzieć, jak znaleźć równanie liniowe w postaci kierunkowej? Zakładamy, że znasz dwa punkty, przez które przechodzi prosta. Pierwszy z nich będzie miał współrzędne (x₁, y₁), a drugi (x₂, y₂). Niewiadomymi są nachylenie a i wyraz wolny b.

Po pierwsze, podstaw współrzędne dwóch punktów do równania kierunkowego prostej:

(1) y₁ = ax₁ + b

(2) y₂ = ax₂ + b

Następnie odejmij pierwsze równanie od drugiego:

y₂ - y₁ = a(x₂ - x₁)

Na koniec podziel obie strony równania przez (x₂ - x₁), aby znaleźć nachylenie:

a = (y₂ - y₁)/(x₂ - x₁)

Po znalezieniu nachylenia można je podstawić do pierwszego lub drugiego równania, aby znaleźć punkt przecięcia z osią y:

y₁ = x₁(y₂ - y₁)/(x₂ - x₁) + b

b = y₁ - x₁(y₂ - y₁)/(x₂ - x₁)

Omni kalkulator równania kierunkowego prostej pozwala na znalezienie równania prostej w tej postaci. Wystarczy podać dwa punkty, przez które przechodzi prosta. Należy postępować zgodnie z procedurą opisaną poniżej:

1. Zapisz współrzędne pierwszego punktu. Załóżmy, że jest to punkt o współrzędnych x₁ = 1 i y₁ = 1.

2. Zapisz również współrzędne drugiego punktu. Przyjmijmy punkt o współrzędnych x₂ = 2 i y₂ = 3.

3. Użyj wzoru na współczynnik kierunkowy, aby znaleźć nachylenie:

   a = (y₂ - y₁)/(x₂ - x₁) = (3-1)/(2-1) = 2/1 = 2

4. Oblicz wyraz wolny. Można również użyć x₂ i y₂ zamiast x₁ i y₁.

   b = y₁ - a · x₁ = 1 - 2 · 1 = -1

5. Umieść wszystkie te wartości razem, aby uzyskać równanie kierunkowe linii prostej:

   y = 2x - 1

6. Możesz także użyć kalkulatora odległości, aby znaleźć dystans między dwoma punktami.

Zazwyczaj możliwe jest znalezienie punktu przecięcia prostej z osią x. Jest to wartość x, przy której prosta przecina oś odciętych (oznacza to wartość x, dla której y równa się 0). Można ją obliczyć w następujący sposób:

0 = ax + b

x = -b/a

Jak możemy zauważyć, jedynym warunkiem, który musi być spełniony, jest to, żeby współczynnik kierunkowy był różny od zera.

Nasz kalkulator równania kierunkowego prostej wyświetli zarówno wartości współrzędnej x, jak i współrzędnej y. Jeśli jednak chcesz dowiedzieć się więcej na ich temat, zalecamy odwiedzenie naszego kalkulatora punktów przecięcia z osią y 🇺🇸.

Zobaczyliśmy już, co to jest równanie kierunkowe prostej, ale aby zrozumieć, dlaczego ta postać jest tak przydatna, powinniśmy znać niektóre zastosowania tego równania w życiu codziennym. Zobaczmy kilka przykładów. Zaczniemy od tych z fizyki, aby móc intuicyjnie zrozumieć, co oznaczają punkty przecięcia z osiami.

Wyobraź sobie samochód poruszający się ze stałą prędkością w twoją stronę. Jego ruch można wykreślić jako zależność odległości między tobą a nim od czasu (jak pokazano powyżej). Oznacza to, że oś x będzie reprezentować czas, a oś y odległość od samochodu. Możesz sobie nawet wyobrazić, że samochód zaczął się poruszać przed uruchomieniem stopera (to znaczy: przed t = 0).

Teraz, jeśli spojrzysz na punkt przecięcia z osią y (x = 0), to zauważysz, że to punkt, w którym zaczęto odmierzać czas, czyli t = 0. Tak więc wartość y w tym punkcie wskaże pozycję początkową (odległość) samochodu względem ciebie. Wartość ta jest, jak omówiliśmy wcześniej, taka sama jak wartość wyrazu wolnego b równania prostej w postaci kierunkowej.

Patrząc teraz na punkt przecięcia z osią x (y = 0), to będzie to punkt, w którym odległość od samochodu do ciebie będzie wynosić 0. Wówczas wartość x w tym punkcie będzie czasem, w którym ty i samochód byliście w tym samym miejscu.

Powyższy przykład samochodu jest bardzo prosty, ale pozwala pomóc zrozumieć, dlaczego postać kierunkowa prostej jest ważna, a dokładniej jakie jest znaczenie punktów przecięcia. W tym artykule omawiamy głównie linie proste, ale punkty przecięcia można obliczyć dla dowolnego rodzaju krzywej (jeśli przecina ona oś).

Jak możemy zauważyć, powyższy przykład nie pasuje do równania liniowego, ale nadal występują oba rodzaje punktów przecięcia z osiami. To samo może się zdarzyć dla każdej innej paraboli lub krzywej innego kształtu.

Jednym z równań, które zapewnia występowanie punktu przecięcia z osią y, ale niekoniecznie z osią x, jest równanie kwadratowe. Jest to przykład krzywej pokazanej na powyższym obrazku. Ma ona maksimum lub minimum (w zależności od orientacji). Jeśli to maksimum znajduje się poniżej osi x lub minimum znajduje się powyżej osi x, nigdy nie będzie punktu przecięcia z osią x.

Jednakże, w przeciwieństwie do ludzi, nie wszystkie równania są równe. Niektóre wzory opisują krzywe, które mogą nigdy nie przecinać osi x, osi y lub obu. Zobaczmy bardziej szczegółowo, jak to może wyglądać.

Możemy wyróżnić 3 grupy równań opisujących krzywe w zależności od tego, czy mają one tylko punkt przecięcia z osią y, tylko z osią x, czy też nie mają żadnego z nich. Pierwsza grupa (tylko punkt przecięcia z osią y) może mieć prawie każdy typ równania, w tym równania liniowe. Dobrym przykładem jest prosta y = 3 (lub dowolna inna stała wartość y z wyjątkiem 0), ponieważ jest to linia równoległa do osi x, a zatem nigdy jej nie dotyka ani nie przecina. Nie próbuj znaleźć takiego punktu przecięcia z wykorzystaniem naszego kalkulatora, ponieważ tego typu równania mogą potencjalnie zepsuć internet.

Druga i trzecia grupa równań są nieco trudniejsze do wyobrażenia i aby je dobrze zrozumieć, musimy wprowadzić pojęcie asymptoty. Asymptota to linia (którą można wyrazić jako równanie liniowe), do której omawiana funkcja lub krzywa zbliża się coraz bardziej, ale nigdy jej nie przecina ani nie dotyka.

Definicja może nie wydawać się całkowicie jasna, ale jeśli spojrzymy na przykładowe równanie, będziemy mieli mniej problemów z jej zrozumieniem. Weźmy równanie y = 1/x. Jeśli spróbujemy znaleźć punkt przecięcia z osią y poprzez podstawienie x = 0, otrzymamy tak zwane wyrażenie niezdefiniowane matematycznie, ponieważ dzielenie przez 0 nie ma sensu.

Jeśli przyjmiemy wartości coraz bliższe 0 (np. 0,1, następnie 0,001, 0,000001, …), możemy zauważyć, że wartość y rośnie bardzo szybko. Tak więc wokół punktu x = 0 wiemy, że y miałoby ogromną wartość, ale ze względu na to, jak działa matematyka, nie ma zdefiniowanej wartości dla tego dokładnego punktu. Czasami ludzie mogą powiedzieć „1/0 = ∞”, ale w rzeczywistości nieskończoność nie jest liczbą, ale koncepcją.

W tym przypadku równanie liniowe x = 0 reprezentuje asymptotę funkcji y = 1/x, co oznacza, że y = 1/x nigdy nie przetnie tej linii, a zatem nie będzie miało punktu przecięcia z osią y. Ogólnie rzecz biorąc, za każdym razem, gdy funkcja ma asymptotę, która leży na jednej z osi, będzie brakowało co najmniej jednego z punktów przecięcia.

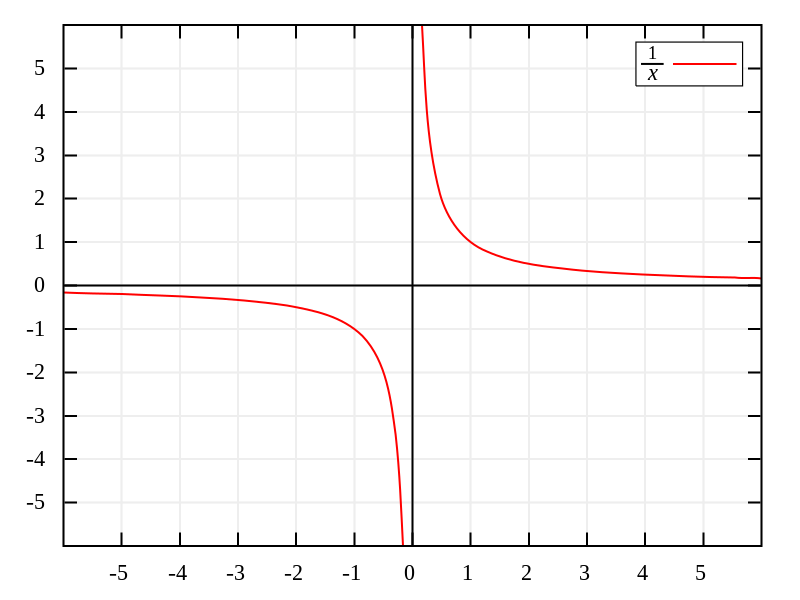
Tak się składa, że przykład, który pokazaliśmy (y = 1/x) również ma asymptotę dla y = 0, tj. leżącą na osi x. Z tego samego powodu, co wcześniej, y = 0 nigdy nie jest osiągalne za pomocą wzoru, ponieważ wymagałoby to x = ∞, a jak powiedzieliśmy wcześniej, jest to niemożliwe, ponieważ nieskończoność jest pojęciem, a nie liczbą.

Zanim przejdziemy do następnego tematu, ważne jest, aby pamiętać, że dokonaliśmy skrajnych uproszczeń, mówiąc o nieskończoności, ale uważamy, że jest to wystarczająco dobre i szybkie podejście dla tych, którzy nie są przyzwyczajeni do koncepcji pracy z nieskończonością w matematyce. Zalecamy, aby dowiedzieć się więcej o właściwych sposobach radzenia sobie z nieskończonościami, zaczynając od niezdefiniowanych wyrażeń w matematyce.

Można by pomyśleć, że użyteczność równań liniowych jest bardzo ograniczona ze względu na ich prostotę. Rzeczywistość jest jednak nieco inna. Równania liniowe są podstawą niektórych z najpotężniejszych metod rozwiązywania problemów minimalizacji i optymalizacji.

Problemy minimalizacyjne są rodzajem problemów, w których chcemy znaleźć sposób, aby jedna ze zmiennych była jak najmniejsza. Zmienną tą może być na przykład różnica między przewidywaniami modelu a rzeczywistością. Tego typu zagadnienia są jednymi z najczęstszych problemów i leżą u podstaw uczenia maszynowego oraz eksperymentów naukowych.

Jedną z najpopularniejszych i najskuteczniejszych metod znajdowania minimalnej wartości równania lub wzoru jest tak zwana metoda Newtona, nazwana na cześć geniusza, który ją wynalazł. Metoda ta polega na wykorzystaniu pochodnych, równań liniowych i punktów przecięcia z osią x:

Metoda ta polega na wybraniu wartości x dla podanego wzoru i obliczeniu pochodnej równania w tym punkcie. Używając pochodnej jako nachylenia równania liniowego oraz korzystając z faktu, że taka prosta przechodzi dokładnie przez punkt (x, y), to możemy też wyznaczyć punkt jej przecięcia z osią x. Jest to jedna z sytuacji, w których przydaje się kierunkowa postać prostej.

Po obliczeniu punktu x ta wartość x jest używana do powtórzenia powyższego procesu określoną liczbę razy, aż dojdziemy do wartości y, która jest równa (albo wystarczająco bliska) zeru. W prawdziwym życiu dojście do dokładnego miejsca zerowego nie jest możliwe w skończonym czasie, więc zazwyczaj ludzie zadowalają się wartością „wystarczająco bliską”.

Jednym z bardzo powszechnych przykładów jest użycie metody najmniejszych kwadratów do dopasowania niektórych danych do wzoru lub trendu. W tym przypadku wartością, którą chcemy zminimalizować, jest suma kwadratów odległości od linii trendu do punktów oznaczających dane, gdzie odległość jest obliczana wzdłuż prostopadłej linii od punktu do linii trendu.

Nie, postać ogólna i postać kierunkowa to dwa różne sposoby opisywania funkcji liniowej:

• Postać kierunkowa to y = ax + b, gdzie a to współczynnik kierunkowy (nachylenie) prostej, a b to wyraz wolny, tj. wartość, przy której linia przecina oś pionową. Na przykład, y = -2x + 3.

• Postać ogólna to Ax + By + C = 0, gdzie A, B, C są liczbami całkowitymi. Na przykład, 2x + y - 3 = 0.

Jeśli chcesz przekształcić równanie w postaci ogólnej do postaci kierunkowej, wykonaj następujące kroki:

1. Zapisz równanie prostej w postaci ogólnej: Ax + By + C = 0.

2. Przenieś Ax i C na prawą stronę tak, aby By pozostało samo po lewej stronie: By = -Ax - C.

3. Podziel obie strony przez B: y = -(A/B)x - (C/B).

4. Jak widać, otrzymaliśmy równanie kierunkowe w postaci y = ax + b z nachyleniem a = -A/B i wyrazem wolnym b = -C/B.

Nachylenie (inaczej gradient) opisuje stromość linii. Nachylenie może być dodatnie, ujemne lub zerowe:

• Nachylenie dodatnie oznacza, że prosta wznosi się od lewej do prawej.

• Ujemne nachylenie oznacza, że prosta biegnie w dół od lewej do prawej.

• Zerowe nachylenie oznacza, że prosta jest pozioma.

Im większa wartość bezwzględna nachylenia, tym szybciej prosta rośnie/spada. W rzeczywistości, wartość nachylenia jest dokładnie tym, o ile prosta wzrasta/spada, gdy x wzrasta o jedną jednostkę.

Współczynnik kierunkowy wynosi a = 1. Aby otrzymać ten wynik, użyj wzoru a = tg(α), gdzie α jest kątem pomiędzy prostą a osią x. Ponieważ tg(45°) = 1, otrzymujemy nachylenie 1, zgodnie z podaną odpowiedzią.