Calculadora do Desvio Padrão da Distribuição Amostral da Média

O cálculo do desvio padrão da distribuição amostral da média (também conhecido como desvio padrão da média da amostra e erro padrão), é uma excelente maneira de entender como o tamanho da amostra influencia o erro de nossas estimativas.

Quando o desvio padrão da distribuição amostral da média é multiplicado por um valor crítico, como o escore padrão ou a estatística t, obtemos uma margem de erro que permite declarar um intervalo de confiança de nossa previsão (mais detalhes podem ser encontrados na nossa calculadora de intervalo de confiança). Portanto, o cálculo do desvio padrão da distribuição amostral da média indica onde poderia estar a média da população.

Antes de mais nada, é importante esclarecer que esse termo também é conhecido como erro padrão.

Também é essencial que você entenda algumas definições e conceitos:

• Estatística: uma estimativa pontual ou característica numérica de uma amostra (ou seja, média da amostra). É diferente de um parâmetro, como a média da população.
• Amostra: um conjunto de dados amostrados aleatoriamente. Em outras palavras, é a distribuição de todos os valores possíveis que uma estatística poderia assumir considerando o tamanho da população.
• Distribuição amostral: essa é uma extensão do conceito anterior. Se você tiver uma população, coletar infinitas amostras de tamanho n e plotar suas médias em um histograma, obterá uma distribuição de probabilidade. Essa distribuição de probabilidade é o que chamamos de distribuição amostral da média e, como qualquer outra distribuição, ela tem sua própria média e desvio padrão.

O diagrama a seguir mostra como você pode gerar uma distribuição amostral da média. Na realidade, não usamos apenas seis amostras, mas um número quase infinito (ou seja, 100.000).

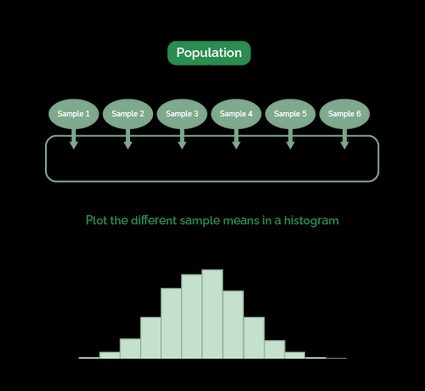
Dito isso, podemos definir a média do desvio padrão como o desvio padrão de uma distribuição de médias (como a mostrada no último diagrama). Além disso, a média dessa distribuição amostral é igual à média da população.

Agora que você conhece o conceito, vamos ver como calcular o desvio padrão da distribuição amostral da média.

A diferença entre uma amostra e uma distribuição amostral é:

• Distribuição amostral: é o termo que normalmente ouvimos referente à distribuição de probabilidade de uma estatística amostrada aleatoriamente. A distribuição amostral da média é um exemplo.
• Amostra: é o conjunto de observações obtidas a partir de uma população. Cada amostra contribui para o cálculo da média, que forma a distribuição amostral.

A fórmula para encontrar o desvio padrão da distribuição amostral da média é a seguinte:

σ_X̄ = σ/√n

onde:

• σ_X̄: desvio padrão da distribuição amostral da média;
• σ: desvio padrão da população; e
• n: tamanho da amostra.

Dissemos anteriormente que, se soubermos a média da distribuição amostral (μ_X̄), também saberemos a média da população (μ), pois elas são iguais (μ_X̄ = μ). Na prática, nunca sabemos μ_X̄, mas podemos estimá-la usando a média da amostra (X̄).

σ_X̄ indica como X̄ se aproxima de μ. Quanto menor σ_X̄, mais próximo μ pode estar de nossa estimativa. Como σ é constante, aumentar o tamanho da amostra é a única maneira de diminuir σ_X̄. Portanto, aumentar n é uma forma de reduzir o erro de amostragem de nossas estimativas. Para saber mais sobre como realizar esse procedimento, acesse a nossa calculadora de erro amostral 🇺🇸.

Sabemos que a média e o desvio padrão da altura de uma determinada população são aproximadamente μ = 161,3 cm e σ = 7,1 cm. Agora, suponha que você colete aleatoriamente amostras de 100 pessoas e obtenha a altura média de cada uma delas. Qual é o desvio padrão da distribuição amostral da média?

Para saber a resposta, siga estas etapas:

1. Insira 7,1 no campo de desvio padrão da população.
2. Insira 100 no campo de tamanho da amostra.
3. É isso aí. A resposta deve ser 0,71. Portanto, o desvio padrão das distribuições amostrais das médias n = 100 é 0,71.

Você pode verificar os resultados usando a fórmula: $σ_{\bar X} = \frac{σ}{\sqrt{n}} = \frac{7{,}1}{\sqrt{100}} = 0{,}71$