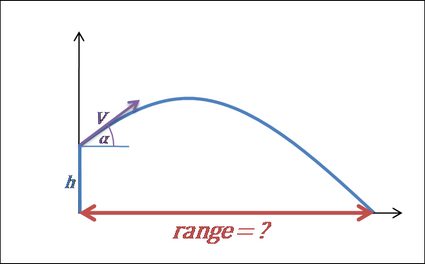
Calculadora de Alcance de Projétil
Com a calculadora de alcance de projétil da Omni, você rapidamente descobrirá até onde pode lançar um objeto. Tudo o que você precisa fazer é inserir os três parâmetros do movimento do projétil: velocidade, ângulo e altura a partir dos quais ele é lançado. Logo, você encontrará o deslocamento horizontal do projétil. Faça experiências com a calculadora e descubra qual ângulo garante a distância máxima de um projétil, ou continue lendo e saiba mais sobre as fórmulas de alcance de projéteis.
🔎 Se quiser encontrar o alcance apenas para um lançamento horizontal (ângulo = 0), você pode usar esta calculadora de alcance de projéteis ou acessar a nossa calculadora de lançamento horizontal de projéteis.
Fórmulas de alcance de um projétil
Vamos dividir as equações em dois casos: quando lançamos o projétil do chão e quando o objeto é lançado a partir de uma altura inicial (por exemplo, mesa, prédio, ponte).
1. Lançamento a partir do solo (altura inicial = 0)
Para encontrar a fórmula para o alcance do projétil, vamos começar com a equação de movimento. O alcance do projétil é a distância percorrida pelo objeto quando ele retorna ao solo (portanto, y = 0):
0 = V₀ × t × sen(α) - g × t²/2
A partir dessa equação, encontraremos t, que é o tempo de voo até o solo:
t = 2 × V₀ × sen(α)/g
Além disso, sabemos que podemos encontrar a distância máxima do projétil a partir da fórmula amplamente conhecida: d = V × t (saiba mais em nossa calculadora de distância). A velocidade, no nosso caso, é a velocidade horizontal Vx = V₀ × cos(α), e o tempo para atingir o solo é um valor que já calculamos:
d = V × t = V₀ × cos(α) × 2 × V₀ × sen(α)/g
d = 2 × V₀² × cos(α) × sen(α)/g
Se você já usou a nossa calculadora de funções trigonométricas 🇺🇸, sabe que sen(2x) = 2sen(x)cos(x), portanto, a fórmula final para a distância é:
d = V₀² × sen(2 × α)/g
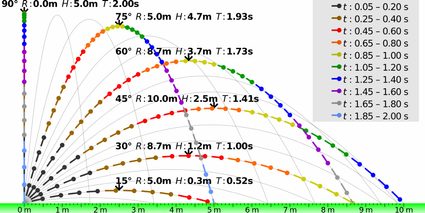
Você descobriu quando a distância é máxima? É quando o termo sen(2α) tem o maior valor possível, ou seja:
sen(2α) = 1 => 2α = 90° => α = 45°
2. Lançamento de uma elevação (altura inicial > 0)
Nesse caso, o tempo gasto voando para cima é menor do que o tempo em que o objeto está caindo. A fórmula para o alcance do projétil é a mesma: a velocidade horizontal (V₀) multiplicada pela equação do tempo de voo (veja mais detalhes na nossa calculadora de tempo de voo 🇺🇸):
Usando a calculadora de alcance de projétil
Vamos descobrir o alcance de projéteis balísticos vulcânicos hipotéticos 🌋:
- Insira a velocidade do projétil. Suponha que uma rocha tenha sido ejetada de um vulcão com uma velocidade de 30 m/s.
- Digite o ângulo. Digamos que o ângulo seja igual a 25°.
- Preencha o campo da altura inicial. Nosso vulcão era relativamente pequeno, e a rocha caiu na lateral do vulcão a uma altitude 100 m menor do que a do ponto de lançamento.
- A calculadora de alcance do projétil mostra a resposta! A distância máxima é de 162,87 m para o nosso exemplo de vulcão. Nossa pedra voou bem longe!
Na realidade, o movimento do projétil é um fenômeno muito mais complicado. A resistência do ar, a forma do objeto, as característica da sua superfície, sua massa etc, são fatores que podem influenciar o alcance de um projétil.
Perguntas frequentes
O que é alcance no movimento de projéteis?
O alcance do projétil é a distância horizontal que o objeto percorrerá a partir do momento em que você o lançar até que ele retorne à mesma altura em que foi lançado. Observe que nenhuma aceleração está agindo nessa direção, pois a gravidade atua apenas na vertical. Para determinar o alcance do projétil, é necessário encontrar a velocidade inicial, o ângulo e a altura. Normalmente, especificamos o alcance horizontal em metros (m).
Como calcular o alcance do projétil?
Imagine que um jogador de futebol chutou a bola do nível do solo em um ângulo de 35° com uma velocidade inicial de 22,0 m/s. Para encontrar o alcance do projétil:
- Pegue a velocidade inicial: V₀ = 22 m/s.
- Identifique o ângulo: α = 35°.
- Suponha que a altura inicial = 0.
- Insira os dados na equação:
d = V₀² × sen(2 × α)/g =
= (22 m/s)² × sen(2 × 35°)/9,81 m/s²
= 46,4 m.
A bola caiu a 46,4 m do jogador.
Qual é a condição para um mínimo alcance de projétil?
O alcance será mínimo se o ângulo de lançamento for 90°. Observe que sen(2 × 90°) = sen(180°) = 0 e, portanto, d = V₀² × sen(180°)/g = 0. Por outro lado, o alcance máximo ocorre para um lançamento com ângulo de 45°.
O alcance do projétil depende da massa?
Não, a massa não afeta o movimento do projétil, e seu valor é irrelevante. No movimento do projétil, parâmetros como a distância percorrida, o tempo gasto pelo projétil e a altura máxima dependem apenas da velocidade inicial, da altura e do ângulo de lançamento.
Qual é o alcance do arremesso de um jogador de basquete de 2 m de altura?
Supondo que a bola tenha sido lançada com uma velocidade de 8,2 m/s e um ângulo de 45°, o alcance do projétil é de 8,48 m. Para calcular isso, você deve:
-
Identificar a altura inicial = 2 m, α = 45° e V₀ = 8,2 m/s.
-
Usar a fórmula:
d = V₀cosα × (V₀senα+√[(V₀senα)²+2gh])/g =8,2 m/s × cos45° × (8,2 m/s × sen45° + √[(8,2 m/s × sen45°)² + 2 × 9,81 m/s × 2 m])/9,81 m/s = 8,48 m.