Calcolatore per l'Area della Superficie dei Solidi

Questo calcolatore per l'area della superficie dei solidi ti aiuta a trovare l'area dei solidi tridimensionali più comuni. Se ti interessa di sapere come si trova un'area della superficie o qual è l'area della superficie laterale, questo calcolatore è qui per aiutarti. L'area della superficie ha una lista gigantesca di applicazioni in ogni campo, come ad esempio l'aerodinamica.

In questo articolo troverai le formule per l'area della superficie di una sfera, un cubo, un cilindro, un cono, una piramide e un prisma rettangolare o triangolare. Ti spiegheremo anche come calcolare l'area della superficie di una sfera come esempio.

L'area della superficie è l'area totale che occupa la superficie di un oggetto. In altre parole, è l'area totale della superficie di un oggetto 3D.

A volte l'area della superficie può essere suddivisa in una somma dell’area della base e quella della superficie laterale. L'area superficiale è l'area di tutti i lati dell'oggetto, esclusi la base e la parte superiore. Questa divisione viene utilizzata per le forme in cui c'è una distinzione ovvia tra la base e le altre parti, ad esempio per un cilindro, un cono, una piramide o un prisma triangolare. Raramente viene applicata ai solidi per i quali non siamo sicuri di quali facce debbano essere trattate come basi (come nel caso di un cubo o di una scatola) e non viene utilizzata per superfici lisce come una sfera.

Il nostro calcolatore per l'area della superficie dei solidi può trovare l'area della superficie di sette diversi solidi. La formula dipende dal tipo di solido.

• Area della superficie di una sfera: A = 4πr², dove r indica il raggio della sfera.

• Area della superficie di un cubo: A = 6a², dove a è la lunghezza del lato.

• Area della superficie di un cilindro: A = 2πr² + 2πrh, dove r è il raggio e h è l'altezza del cilindro.

• Area della superficie di un cono: A = πr² + πr√(r² + h²), dove r è il raggio e h è l'altezza del cono.

• Area della superficie di un prisma rettangolare (scatola): A = 2(ab + bc + ac), dove a, b e c sono le lunghezze dei tre lati del cuboide.

• Area della superficie di un prisma triangolare: A = 0,5 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)) + h × (a + b + c), dove a, b e c sono le lunghezze dei tre lati della base del prisma triangolare e h è l'altezza (lunghezza) del prisma.

• Area della superficie di una piramide: A = l × √(l² + 4 × h²) + l², dove l è la lunghezza del lato della base quadrata e h è l'altezza della piramide.

Ma da dove vengono queste formule? Come si trova l'area superficiale delle forme 3D di base? Continua a leggere e lo scoprirai!

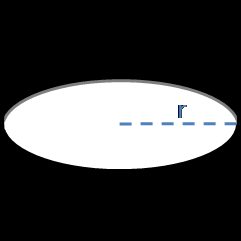
Per calcolare l'area della superficie di una sfera, tutto ciò che devi sapere è il suo raggio, ovvero il suo diametro.

• A = 4 × π × r²

  dove r è il raggio

Poiché sappiamo che il diametro di una sfera è uguale a due raggi d = 2r, possiamo trasformare l'equazione in un'altra forma:

• A = 4 × π × (d / 2)² = π × d²

  dove d è il diametro della sfera.

La formula derivativa dell'area superficiale richiede un'integrazione. Se la derivazione di queste formule ti interessano, dai un'occhiata a questa prova.

Per trovare l'area della superficie di un cilindro, devi avere due valori: il raggio (o diametro) della base, e l'altezza del cilindro. L'equazione generale è la solita — area delle basi più area delle superfici laterali. Nel nostro caso, le basi sono dei cerchi.

• A = 2πr² + 2πrh

Da dove deriva questa formula? L'equazione dell'area della superficie di un cilindro può essere scritta come:

• A = A(laterale) + 2 × A(base)

È facile trovare l'area della base — ricordiamo la nota formula per l'area di un cerchio: A(base) = π × r². Ma qual è la forma dell'area della superficie laterale? Prova a immaginare di "dispiegarla". La riconosci? È un rettangolo! La lunghezza di un lato è l'altezza del cilindro, mentre il secondo è la circonferenza del cilindro.

• A(base) = π × r²
• A(laterale) = h × (2 × π × r)

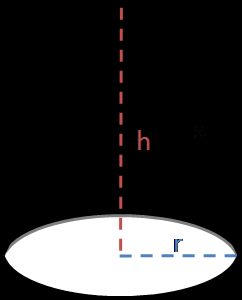
Possiamo dividere l'area della superficie di un cono in due parti:

• A = A(laterale) + A(base), poiché abbiamo una sola base, a differenza di un cilindro.

La base è di nuovo l'area di un cerchio A(base) = π × r², ma le origini della superficie laterale forse non sono così ovvie:

• A(laterale) = π × r × √(r² + h²)

Diamo un'occhiata a questo derivato passo per passo:

1. Immagina di stendere la superficie laterale in piano. Si tratta di un settore circolare, ovvero la parte di un cerchio di raggio s (s è l'altezza del cono).

2. Per il cerchio con raggio s, la circonferenza è uguale a 2 × π × s. La lunghezza dell'arco del settore è uguale a 2 × π × r.

3. L'area di un settore, che è la superficie laterale di un cono, è data dalla formula:

• A(laterale) = (s × (lunghezza dell'arco)) / 2 = (s × 2 × π × r) / 2 = π × r × s

  La formula può essere ricavata dalle proporzioni, poiché il rapporto tra le aree delle forme è uguale al rapporto tra la lunghezza dell'arco e la circonferenza:

  (Area del settore) / (area del cerchio grande) = (lunghezza dell'arco) / (circonferenza del cerchio grande) quindi:

  (Area del settore) / (π × s²) = (2 × π × r) / (2 × π × s)

  (Area del settore) = (π × s²) × (2 × π × r) / (2 × π × s)

• A(laterale) = π × r × s

  Per trovare il termine mancante di questo rapporto, puoi provare anche il nostro calcolatore del rapporto 🇺🇸!

4. Di solito non abbiamo il valore s ma h, che è l'altezza del cono. Questo non è affatto un problema! Possiamo facilmente trasformare la formula utilizzando il teorema di Pitagora:

• r² + h²= s² quindi, elevando al quadrato, otteniamo s = √(r² + h²)

  La formula dell'area superficiale laterale è quindi la seguente:

• A(laterale) = π × r × √(r² + h²)

5. Infine, aggiungi le aree della base e della parte laterale per trovare la formula finale dell'area della superficie di un cono:

• A = A(laterale) + A(base) = π × r × s + π × r² date r e s oppure
• A = π × r × √(r² + h²) + π × r² dati r e h.

L'area della superficie di un cubo 🇺🇸 è la più semplice che tu possa immaginare: ogni lato è un quadrato! Poiché ogni cubo ha sei facce quadrate identiche, l'area della superficie è uguale a:

• A = 6 × (area del lato)

Poiché l'area di un quadrato è il prodotto della lunghezza dei suoi lati, la formula finale per l'area della superficie di un cubo è:

• A = 6 × l²

  dove l è il lato di un quadrato da elevare al quadrato.

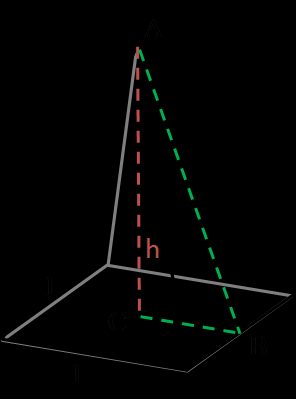
Una piramide è un solido 3D con una base poligonale e facce laterali triangolari. Quando si sente parlare di una piramide, di solito si suppone che si tratti di una piramide regolare elevare al quadrato. Ma a seconda della forma della base, potrebbe anche essere una piramide esagonale o una piramide rettangolare. Regolare significa che ha un poligono regolare di base ed è una piramide retta (il vertice si trova direttamente sopra il centroide della base), mentre quadrato — significa che ha questa forma come base. Questa è l'opzione che abbiamo utilizzato come piramide in questo calcolatore per l'area della superficie.

La formula per l'area della superficie di una piramide è:

• A = l × √(l² + 4 × h²) + l², dove l è il lato della base e h è l'altezza della piramide.

Anche in questo caso, possiamo dividere l'equazione in:

A = A(base) + A(laterale) = A(base) + 4 × A(faccia laterale)

La base ha la forma di un quadrato, quindi A(base) = l². Per calcolare l'area della superficie laterale, partiamo dall'area di una faccia triangolare:

1. Per trovare l'altezza del triangolo, avremo bisogno di nuovo della formula dell'ipotenusa:

   c = √(a² + b²)

2. Calcola l'ipotenusa del triangolo ABC (che è allo stesso tempo l'altezza della faccia del triangolo):

   c = √(h² + (l/2)²) = √(h² + l²/4)

3. L'area di un triangolo (nel nostro caso si tratta di un triangolo isoscele) può essere calcolata in questo modo:

   A = altezza × base / 2

   quindi:

   A(faccia laterale) = √(h² + l²/4) × l / 2

4. Quindi la formula finale per l'area della superficie di una piramide è:

   A = l² + 4 × √(h² + l²/4) × l / 2 = l² + 2 × l × √(h² + l²/4)

   A = l² + l × √(4 × h² + l²)

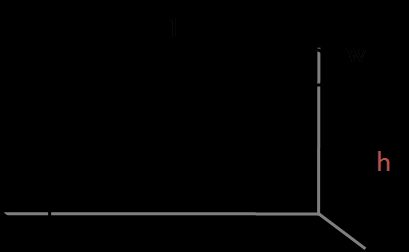
Per calcolare l'area della superficie di un prisma rettangolare, basta calcolare le aree dei lati rettangolari:

• A = 2 × (A1 + A2 + A3)

  dove:

  • A1 = l × w;
  • A2 = w × h; e
  • A3 = l × h.

Quindi, la formula finale è:

A = 2 × (l × w + w × h + l × h)

Per capire da dove deriva la formula dell'area superficiale di un prisma triangolare, diamo un'occhiata a questo derivato:

1. In questo caso, l'area della superficie laterale è facile da calcolare. Come puoi vedere dall'immagine, si tratta di tre rettangoli con un lato in comune:

   A(laterale) = a × h + b × h + c × h = h × (a + b + c)

   che possiamo anche scrivere in breve come:

   A(laterale) = h × P, dove P è il perimetro di un triangolo di base

2. Quindi, trova l'area di una base triangolare. Puoi farlo in molti modi, a seconda dei dati che ti vengono forniti. Nel nostro calcolatore, abbiamo implementato il calcolo basato sulla formula di Erone 🇺🇸 — si usa quando si hanno tre lati di triangolo (LLL).

   A(base) = 0,25 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)))

3. La formula finale dell'area della superficie di un prisma triangolare:

   A = A(laterale) + 2 × A(base)

   A = h × (a + b + c) + 0,5 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c))

Puoi calcolare la superficie di qualsiasi solido, ad esempio del tuo corpo — non è necessario che sia una semplice forma geometrica! Se l'area superficiale esterna di un corpo umano ti incuriosisce, dai un'occhiata a questo calcolatore della superficie corporea.

Se vuoi trovare l'area della superficie di una sfera, devi seguire questi passaggi:

1. Determina il raggio della sfera. Supponiamo un raggio di 10 cm;

2. Inserisci questo valore nella formula:

   A = 4πr²;

3. Calcola il risultato:

   A = 4π × 10² = 1256 cm²; e

4. Puoi anche utilizzare il calcolatore per l'area della superficie dei solidi di Omni per trovare il raggio della sfera se conosci la sua area.

Le unità di misura dell'area della superficie sono sempre unità quadrate di lunghezza. Ad esempio, puoi esprimerla in cm², in², ft², m², ma anche in acri e ettari.

Se vuoi trovare il volume di uno di questi solidi, usa il nostro calcolatore del volume per farlo.

Per convertire l'area della superficie di un cubo nella lunghezza dei suoi lati, segui questi passaggi:

1. Scrivi l'area del tuo cubo;
2. Dividila per sei. Il risultato è l'area di una faccia;
3. Prendi la radice quadrata del numero ottenuto al passo 2; e
4. Questa è la lunghezza di ogni lato del cubo. Ben fatto!

Per dedurre il raggio di una sfera dalla sua area della superficie:

1. Scrivi l'area della superficie della sfera;
2. Dividila per *4π ≈ 12,566;
3. Prendi la radice quadrata: **√(Area / 4π)*; ed
4. Ecco fatto — questo è il raggio! Puoi verificare il tuo risultato utilizzando un calcolatore per l'area della superficie dei solidi online.

La risposta è 314,16 cm sq. Per ricavare questo risultato, ricordiamo che la formula dell'area della superficie di un cilindro è:

Area = 2πr(r + h)

Inserendo r = h = 5, otteniamo Area = 100π ≈ 314,1592. Ricorda le unità di misura! Poiché sia r che h sono in cm, l'area è in cm sq.