Calculadora de Segmentos Proporcionais

A calculadora de segmentos proporcionais da Omni ajudará você a calcular as coordenadas do ponto que particiona o segmento de reta em uma determinada proporção. Este artigo explorará o que é um segmento de reta orientado, como particionar um segmento de reta com uma determinada proporção, a fórmula de partição do segmento e algumas perguntas frequentes.

Se você estiver particionando seu segmento de reta em duas metades, nossa calculadora de ponto médio será igualmente útil.

Um segmento de reta $AB$ é uma parte de uma reta limitada por dois pontos finais $A$ e $B$ onde $A \neq B$. Um segmento de reta orientado $\overrightharpoon{AB}$ é um segmento de reta com uma direção definida, que também pode ser chamado de segmento de reta orientado de $A$ para $B$.

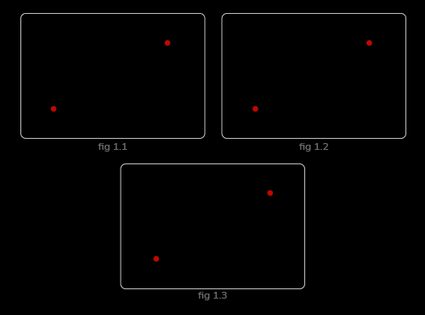
Embora o segmento de reta $AB$ também possa ser escrito como $BA$, o mesmo não ocorre com o segmento de reta orientado $\overrightharpoon{AB}$. Isso ocorre porque $\overrightharpoon{AB}$ é orientado de $A$ para $B$, enquanto $\overrightharpoon{BA}$ é orientado de $B$ para $A$.

Na próxima seção, responderemos à pergunta que está na sua mente: como dividir um segmento em determinadas proporções?

Um ponto $P$ situado no segmento de reta orientado $\overrightharpoon{AB}$ se dividirá em dois segmentos de reta. Há duas maneiras de dividir um segmento de reta:

1. Internamente, quando o ponto $P$ está em algum lugar dentro do segmento $\overrightharpoon{AB}$; e
2. Externamente, quando o ponto $P$ está localizado em uma reta paralela ao segmento de reta, também conhecida como segmento de reta estendido $\overrightharpoon{AB}$.

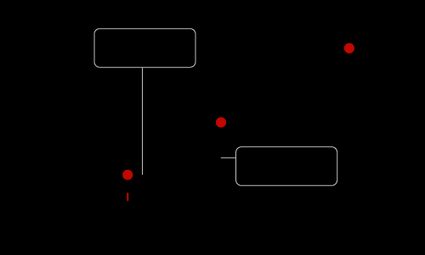
Para que você possa particionar o segmento de reta $\overrightharpoon{AB}$ internamente na relação $m:n$, o ponto $P(p_x,p_y)$ deve estar em $\overrightharpoon{AB}$ de modo que ele esteja localizado na posição $\frac{m}{m+n}$ distante de $A$ e $\frac{n}{m+n}$ distante de $B$.

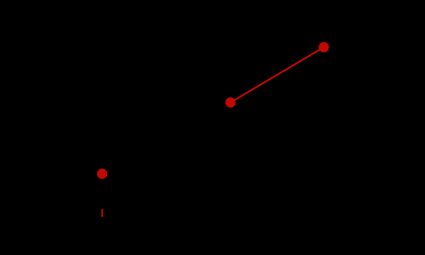
Por outro lado, para particionar o segmento de reta $\overrightharpoon{AB}$ externamente na relação $m:n$, o ponto $P(p_x,p_y)$ deve estar no segmento de reta estendido $\overrightharpoon{AB}$ de forma que ele esteja localizado na posição $\frac{m}{m-n}$ distante de $A$ e $\frac{n}{m-n}$ distante de $B$.

Agora que você conhece o conceito de dividir um segmento de reta em uma razão, vamos montar uma fórmula para um segmento de reta orientado dividido por qualquer ponto $P$.

Para a partição interna de $\overrightharpoon{AB}$ temos:

E para a partição externa de $\overrightharpoon{AB}$ ficamos com:

onde:

• $P$ é qualquer ponto de referência para particionar o segmento de reta orientado $\overrightharpoon{AB}$;
• $p_x,p_y$ são as coordenadas x e y do ponto $P$;
• $m,n$ é a razão $m:n$ na qual ponto $P$ divide $\overrightharpoon{AB}$;
• $x_1,y_1$ são as coordenadas x e y do ponto final $A$ de $\overrightharpoon{AB}$; e
• $x_2,y_2$ são as coordenadas x e y do ponto final $B$ de $\overrightharpoon{AB}$.

Agora que você conhece a fórmula da proporção de segmentos de reta, vamos discuti-la mais detalhadamente, juntamente com alguns exemplos de cálculo de partição de segmentos.

Para encontrar o ponto P(p_x, p_y) que divide internamente o segmento de reta AB na proporção m:n, siga estes passos:

1. Calcule p_x usando p_x = (mx₂ + nx₁)/(m + n), onde x₁ e x₂ são as coordenadas x de A e B, respectivamente.
2. Determine p_y usando p_y = (my₂ + ny₁)/(m + n), onde y₁ e y₂ são as coordenadas y de A e B, respectivamente.

Para encontrar o ponto P(p_x, p_y) que divide externamente o segmento de reta AB na razão m:n, siga estes passos:

1. Calcule p_x usando p_x = (mx₂ - nx₁)/(m - n), onde x₁ e x₂ são as coordenadas x de A e B, respectivamente.
2. Encontre p_y usando p_y = (my₂ - ny₁)/(m - n), onde y₁ e y₂ são as coordenadas y de A e B, respectivamente.

Por exemplo, considere um segmento de reta $\overrightharpoon{AB}$ com os pontos finais $A(1,2)$ e $B(4,6)$. A direção desse segmento seria de $A$ a $B$. Para encontrar um ponto que divida esse segmento internamente na proporção $2:3$, podemos usar a fórmula de partição interna da seguinte forma:

Observe que dizer que o ponto $P(2{,}2,3{,}6)$ divide $\overrightharpoon{AB}$ na proporção $2:3$ é o mesmo que dizer que o ponto $P(2{,}2,3{,}6)$ se encontra ${\frac{2}{5}}$ distante do ponto final $A(1,2)$ e ${\frac{3}{5}}$ distante do ponto final $B(4,6)$.

Agora, se você quiser dividir o mesmo segmento de reta externamente na mesma proporção, empregaremos a fórmula para partição externa do segmento de reta:

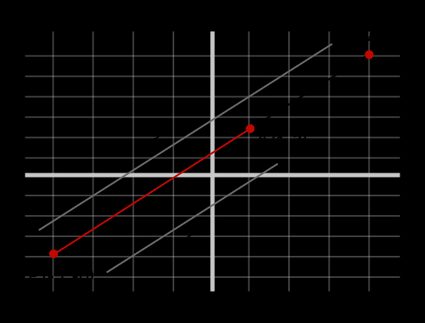
Você vê como é fácil dividir um segmento de reta em uma determinada proporção? 😉 Vá em frente, tente alguns problemas práticos e domine esse método! Você sempre pode verificar seus resultados usando essa calculadora para dividir segmentos de reta.

Essa calculadora de proporções de segmentos de reta orientados é útil para que você encontre o ponto que divide um segmento de reta em uma proporção determinada.

1. Escolha o tipo de partição entre interna e externa no campo A reta é particionada.... Por padrão, a definimos como uma partição interna.

2. Insira as coordenadas dos pontos finais do segmento. Certifique-se de que você está escrevendo a direção do segmento de reta corretamente. Nessa calculadora, a direção é sempre de $A(x_1,y_1)$ a $B(x_2,y_2)$.

3. Esse passo depende de você querer encontrar o ponto ou a proporção:

   • Se a razão for o valor dado, insira a razão dada nos campos correspondentes, e as coordenadas do ponto aparecerão em seus respectivos campos, juntamente com um gráfico útil. Caso contrário, deixe os campos da razão vazios.
   • Se as coordenadas do ponto forem o valor dado, insira estas coordenadas nos campos correspondentes, e a razão resultante aparecerá na parte inferior.

Agora você tem uma ferramenta simples que te ajuda a calcular a partição de um segmento de reta sempre que precisar! Consulte também nossa calculadora da razão de ouro ou calculadora de ponto final para obter mais cálculos de partição de segmentos de reta.

Se você souber as coordenadas das extremidades do segmento de reta, poderá facilmente encontrar seu ponto médio (x_m, y_m) usando estes passos:

1. Calcule a média das coordenadas x dos pontos extremos para obter a coordenada x do ponto médio. x_m = (x₁ + x₂)/2.
2. Determine a média das coordenadas y dos pontos extremos para obter a coordenada y do ponto médio. y_m = (y₁ + y₂)/2.
3. Verifique esses resultados usando nossa calculadora de ponto médio ou calculadora de proporções de segmentos de reta orientados.

Para dividir um segmento de reta AB em três partes iguais, você precisa encontrar dois pontos P(p_x, p_y) e Q(Q_x, Q_y) em AB, de modo que cada um deles divida AB nas razões 1:2 e 2:1:

1. Calcule a coordenada x p_x do ponto P usando a fórmula p_x = (2x₂ + x₁)/3, em que x₁ e x₂ são as coordenadas x de A e B, respectivamente.

2. Calcule a coordenada y do ponto P usando p_y = (2y₂ + y₁)/3, onde y₁ e y₂ são as coordenadas y de A e B, respectivamente.

3. Determine a coordenada x q_x do ponto Q usando q_x = (x₂ + 2x₁)/3.

4. Determine a coordenada y q_y do ponto Q usando q_y = (y₂ + 2y₁)/3.

5. Combine essas coordenadas para obter os pontos P(p_x, p_y) e Q(q_x, q_y).

Um ponto P situado a um terço de distância a partir do ponto final A no segmento de reta AB o dividirá na razão 1:2. Para encontrar esse ponto, siga estas etapas simples:

1. Calcule a coordenada x p_x desse ponto usando a fórmula p_x = (2x₂ + x₁)/3, onde x₁ e x₂ são as coordenadas x de A e B, respectivamente.

2. Calcule a coordenada y p_y desse ponto usando p_y = (2y₂ + y₁)/3, onde y₁ e y₂ são as coordenadas de y de A e B, respectivamente.

3. Combine as coordenadas de x e de y para obter o ponto desejado P(p_x, p_y).